Файл: Руководство к лабораторным работам по дисциплине Теория управления для студентов по направлению Т. 02 Автоматика и управление в технических системах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 106
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Что такое «Δ»?
Какое допустимое значение может принимать перерегулирование?
Какое количество колебаний приемлемо в системах управления?
Лабораторная работа 8
Исследование элементарных нелинейных звеньев
Цель работы: исследование базовых нелинейных блоков и их выходных характеристик.
Краткие теоретические сведения.
Нелинейной системой называется такая система, в состав которой входит хотя бы одно звено, описываемое нелинейным уравнением. Такое звено называется нелинейным звеном или нелинейным элементом.
Путем эквивалентного преобразования структурных схем и нелинейных звеньев большое число нелинейных систем можно представить в виде замкнутого контура с последовательным включением нелинейного элемента (НЭ) и линейной части (ЛЧ), как показано на рис.29.
 |
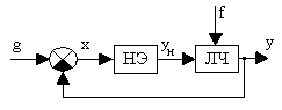Рис.29. Функциональная схема нелинейной системы:
НЭ - нелинейный элемент; ЛЧ - линейная часть
Классификация нелинейных элементов и систем. Нелинейные звенья классифицируются по различным признакам. Наибольшее распространение получила классификация по статическим и динамическим характеристикам, так как в системах чаще всего нелинейности приходится учитывать в виде характеристик. Эти характеристики могут быть как однозначными, так и двузначными (петлевыми), симметричными и несимметричными относительно начала координат.
Различают следующие основные типы нелинейных звеньев.
Нелинейные звенья с гладкими криволинейными характеристиками. Примеры таких характеристик приведены на рис.30.
 |
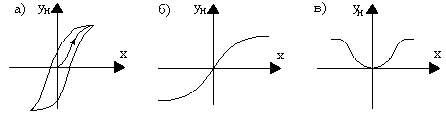Рис.30. Гладкие криволинейные характеристики:
а - гистерезисная; б, в - усилительные
На рис.30,а изображена двузначная гистерезисная (запаздывающая) характеристика. Характеристика (рис.30,б) отображает насыщение или ограничение и соответствует реальному амплитудному усилителю, а характеристика (рис.30,в) - реальному усилителю мощности. Характеристики (рис.30,а и б) - нечетно-симметричные, а характеристика (рис.30,в) - четно-симметричная.
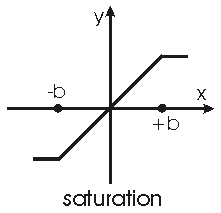
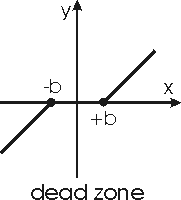
Нелинейные звенья с кусочно-линейными характеристиками. Некоторые из таких характеристик представлены на рис.31.
 |
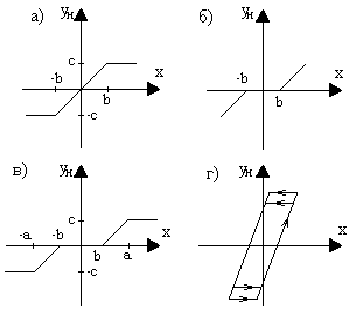Рис.31. Кусочно-линейные характеристики:
а - с насыщением; б - с зоной нечувствительности;
в - с насыщением и зоной нечувствительности; г - люфт
Характеристика (рис.31,а) отображает насыщение, характеристика (рис.31,б) - зону нечувствительности, а характеристика (рис.31,в) соответствует звену, обладающему одновременно зоной нечувствительности и насыщением. Характеристика (рис.31,г) позволяет учесть люфт или зазор кинематической передачи.
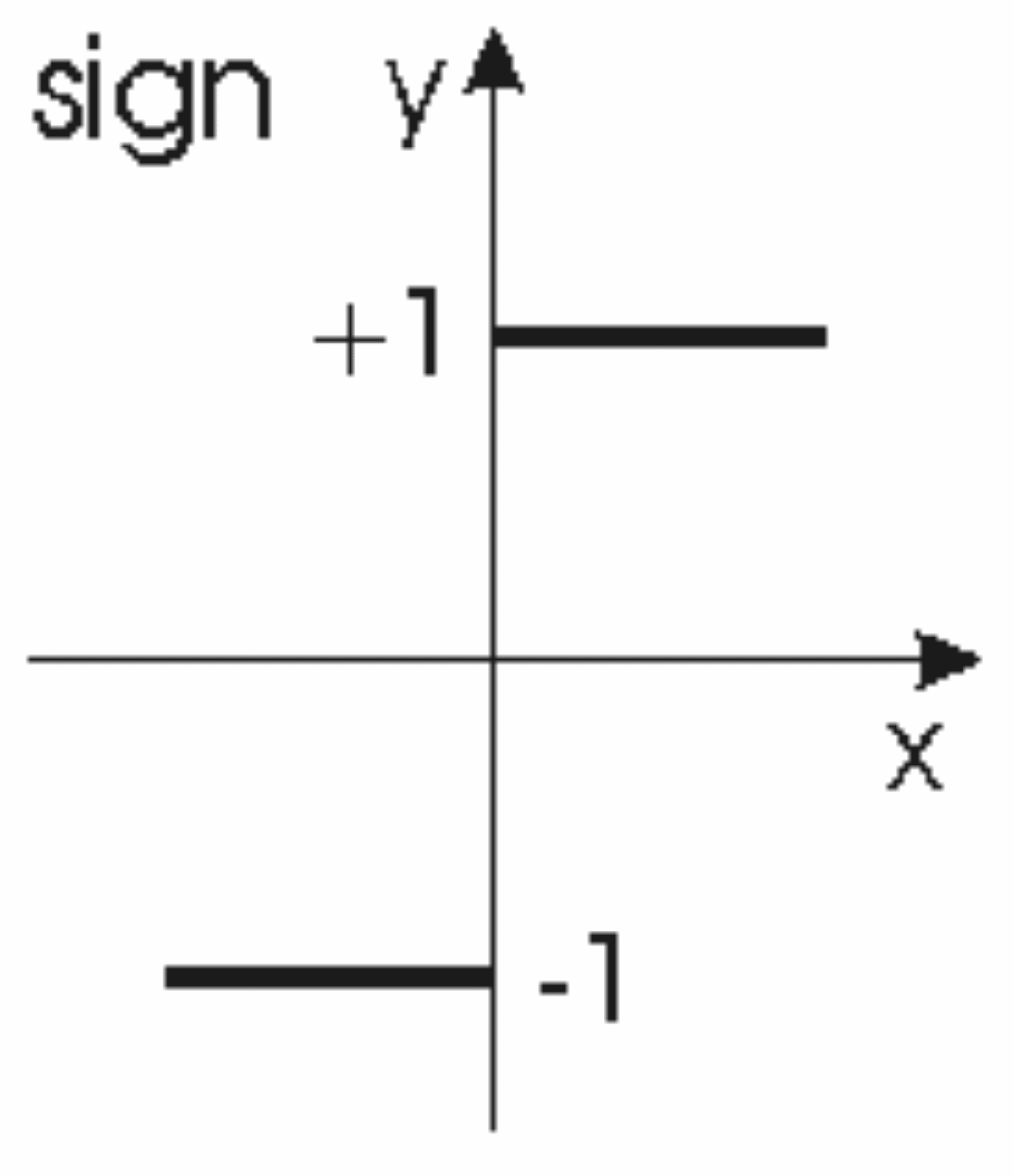
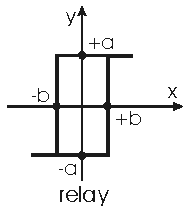
Релейные звенья - это элементы, которые на своем выходе выдают конечное число фиксированных значений. Три наиболее типовые релейные характеристики изображены на рис.32.
 |
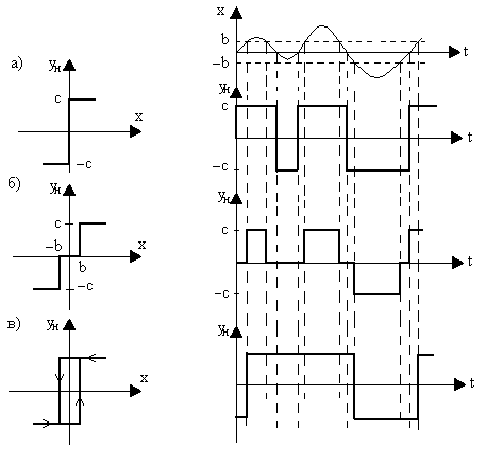Рис.32. Релейные характеристики:
а - идеальная; б - с зоной нечувствительности; в - гистерезисная
Характеристика (рис.32,а) соответствует идеальному двухпозиционному реле, характеристика (рис.32,б) - трехпозиционному реле с зоной нечувствительности, а характеристика (рис.32,в) - двухпозиционному поляризованному реле.
Кроме того, на рис.32 показано прохождение непрерывного сигнала через соответствующие типы реле. Откуда следует, что коэффициент передачи реле зависит от величины входного воздействия.
Для улучшения динамических свойств систем специально созданы нелинейные звенья с опережающими двузначными статическими характеристиками.
Часто встречаются элементы с несимметричными относительно начала координат статическими характеристиками.
Задание и порядок проведения работы
-
Открыть библиотеку Nonlinear. Исследовать типовые нелинейности, указанные в табл.8. -
В соответствии с вариантом настройте их параметры. Изучите статические характеристики типовых нелинейностей, подавая на вход гармонический сигнал. -
Статические характеристики нелинейностей фиксируются с помощью блока "ХУ Graph". Для правильного отображения сигналов следует брать амплитуду синусоидального колебания чуть больше заданного "верхнего уровня". -
По полученным результатам сделайте выводы о физическом смысле этих типовых нелинейных характеристик.
Таблица 8
 Релейная характеристика | | |||
 Характеристика с зоной насыщения | № | b | ||
| 1 | 0,7 | |||
| 2 | 1,3 | |||
| 3 | 2,8 | |||
| 4 | 3,5 | |||
| 5 | 4,2 | |||
| 6 | 5,6 | |||
| 7 | 6,9 | |||
| 8 | 1,7 | |||
| 9 | 2,3 | |||
| 10 | 0,9 | |||
| 11 | 3,7 | |||
| 12 | 5,2 | |||
 Характеристика с зоной нечувствительности | № | b | ||
| 1 | 2,3 | |||
| 2 | 1,7 | |||
| 3 | 0,3 | |||
| 4 | 4,8 | |||
| 5 | 3,4 | |||
| 6 | 5,6 | |||
| 7 | 2,1 | |||
| 8 | 6,9 | |||
| 9 | 3,5 | |||
| 10 | 5,4 | |||
| 11 | 2,8 | |||
| 12 | 6,9 | |||
 Характеристика с гистерезисом | № | a | b | |
| 1 | 2 \ | 0,7 | ||
| 2 | 1,1 | 1,4 | ||
| 3 | 2 | 2,8 | ||
| 4 | 0,5 | 0,9 | ||
| 5 | 3,3 | 3,7 | ||
| 6 | 0,9 | 1,5 | ||
| 7 | 3,7 | 4,3 | ||
| 8 | 2,2 | 2,6 | ||
| 9 | 1,5 | 3,1 | ||
| 10 | 4,8 | 3,7 | ||
| 11 | 8,9 | 2,5 | ||
| 12 | 5,3 | 1,3 | ||
Контрольные вопросы
-
Какие Вам известны типовые нелинейности? -
Приведите примеры и поясните физическую природу нелинейных эффектов в САУ. -
Что называется статической характеристикой и с какой целью ее определяют? -
В каких случаях можно и когда нельзя осуществлять линеаризацию нелинейные статических характеристик? -
Как построить графически статическую характеристику соединения: линейных и нелинейных звеньев, которые включены:
-
последовательно; -
параллельно; -
с помощью обратной связи?
-
По каким признакам различаются нелинейные системы от линейных систем? Приведите несколько примеров.
Лабораторная работа 9
Исследование релейных систем автоматического управления
методом фазовой плоскости
Цель работы: исследование динамики нелинейных систем второго порядка методом фазовой плоскости.
Краткое теоретическое описание
Метод фазовой плоскости используется для исследования систем второго порядка и заключается в построении фазовых портретов на плоскости. Для этого из уравнений состояния исключается время, и определяются уравнения фазовых кривых.
Для изображения процессов на фазовой плоскости нелинейное уравнение, описывающее систему, заменяют эквивалентными уравнениями первого порядка вида
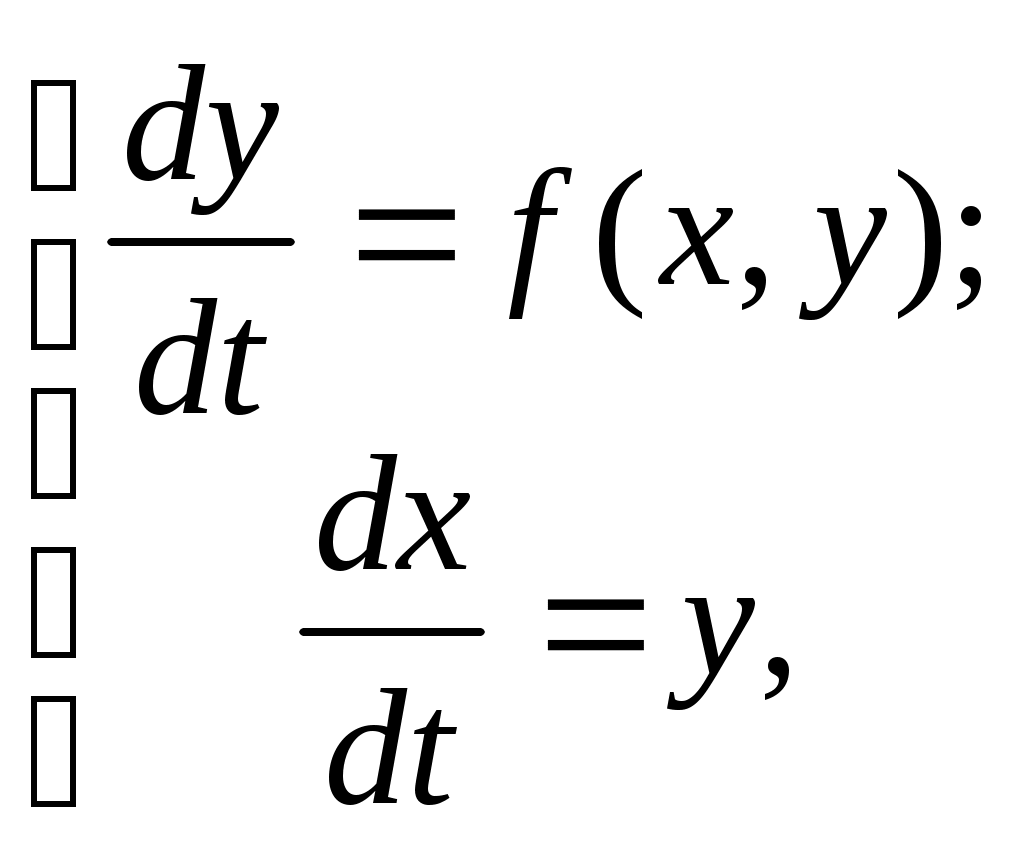
где x, y - координата системы и ее первая производная; f(x, y) - нелинейная функция.
Разделив первое из уравнений на второе, получим дифференциальное уравнение, из которого исключено время t:
Решение данного уравнения
y = F(x)
определяет уравнение фазовой траектории, которая графически изображается на фазовой плоскости (x, y). Каждой совокупности начальных условий (x0, y0) соответствует свое решение и своя фазовая траектория. Семейство фазовых траекторий характеризует все возможные виды переходных процессов в данной системе управления при любых начальных условиях и образует ее фазовый портрет.
Если по линейной теории система неустойчивая и процесс расходится, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Картина фазовых траекторий для такой системы изображена на рис.33,а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе, но далее они приближаются асимптотически к замкнутому контуру ограниченных размеров. К
нему же приближаются и все спирали, находящиеся вне контура. Такого рода замкнутый контур представляет собой особый вид линий на фазовой плоскости и называется устойчивым предельным циклом. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x и скорости ее изменения y. Для определения периода автоколебаний необходимо решить уравнение системы во времени.
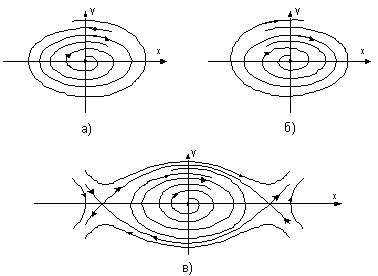
Рис.33. Фазовые траектории нелинейных систем:
а - устойчивый предельный цикл; б - неустойчивый предельный цикл;
в - фазовый портрет системы с сепаратрисами
Замкнутые фазовые траектории на фазовой плоскости называются предельными циклами, которые могут быть как устойчивыми (рис.33,а), так и неустойчивыми (рис.33,б). К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям.
В различных частях фазовой плоскости фазовые траектории нелинейной системы могут быть различными (рис.33,в). Линии, разделяющие фазовую плоскость на участки с различными фазовыми траекториями, называются сепаратрисами. Поведение системы в каждой области фазовой плоскости описывается своим дифференциальным уравнением.
Кроме того, для фазового портрета нелинейных систем с разрывными характеристиками характерно наличие линий переключения, которые также разделяют фазовую плоскость на ряд областей с различными фазовыми траекториями. При этом начальные значения переменных на каждом участке определяются через их конечные значения на предыдущем участке. Линии переключения характеризуются узловыми точками разрывных характеристик нелинейных элементов.
Задание и порядок проведения лабораторной работы
Первая часть
-
В соответствии со структурной схемой на рис.34 смоделируйте систему управления, у которой реле имеет характеристику вида рис.35, а передаточная функция задана соотношением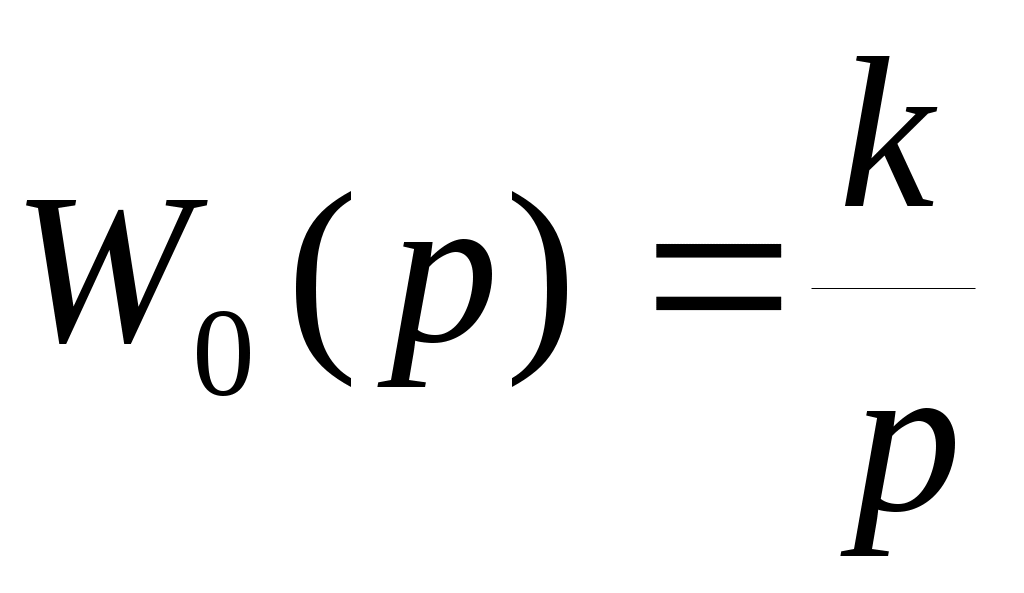
. Значение коэффиента передачи (k) возьмите из табл.9.
 |  |
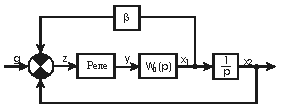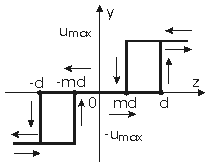| Рис.34 | Рис.35 |