Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 260
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.6. Установить плоскость поляризации излучения параллельно плоскости падения. Повторить пункт 3.5.
3.7. Построить теоретические зависимости энергетических коэффициентов пропускания от угла падения для плоскопараллельной стеклянной пластины по формулам ((54)–(57)) с учетом отражения от двух граней пластины. На этих же графиках построить соответствующие экспериментальные зависимости с учетом статистической обработки результатов с доверительной вероятностью 90%.
3.8. Оценить по экспериментальным зависимостям угол Брюстера и сравнить с рассчитанным значением.
4. Контрольные вопросы и задания
-
Сформулируйте граничные условия для векторов напряжённости электрического и магнитного полей волны. -
Какие физические факторы определяют значение угла Брюстера? -
Почему экспериментальная проверка формул Френеля может быть выполнена наиболее эффективно при углах Брюстера? -
Естественный свет падает на поверхность стекла (n=1.5) под углом Брюстера. Определить степень поляризации преломлённого луча. -
Найти степень поляризации узкого пучка лучей естественного света при прохождении плоскопараллельной пластины из стекла (n=1.5) если пучок падает на пластину под углом Брюстера. -
Найти азимуты колебаний в отражённых и преломлённой волнах, если азимут колебаний в падающей волне α0, а угол падения –Θ0. -
На поверхность стекла (n=1.5) под углом 450 падает линейно поляризованная волна. Найти коэффициенты отражения и пропускания, если: а) вектор напряжённости электрического поля перпендикулярен плоскости падения; б) колеблется в плоскости падения. -
Найти область углов падения линейно поляризованной волны из воздуха на поверхность воды (n=1.33), при которой коэффициент отражения больше 0.5. Рассмотреть случаи, когда плоскость поляризации падающей волны совпадает с плоскостью падения, перпендикулярна ей, падающий свет естественный. -
Из воды (n=1.33) на границу раздела с воздухом под углом 600 падает световая волна. Найти критический угол и сдвиги фаз колебаний напряжённости электрического поля φ┴ и φ║.
Лабораторная работа
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА
ЦЕЛЬ РАБОТЫ: изучение одного из наиболее простых методов определения показателя преломления прозрачного вещества; ознакомление с работой микроскопа.
ПРИНАДЛЕЖНОСТИ: микроскоп, штангенциркуль, набор прозрачных плоскопараллельных пластинок.
1. Вывод основного соотношения
В основу метода измерения показателя преломления в данной работе положена зависимость параметров оптического изображения данного предмета от показателя преломления окружающей среды. Связь размеров предмета и изображения находится с помощью закона Снеллиуса, вывод которого из граничных условий приведён в предыдущей работе (соотношение 13) .
Р
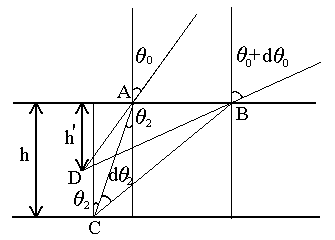
ассмотрим следующую задачу. На внутренней стороне стеклянной пластинки в точке С находится предмет. Толщина пластинки h, показатель преломления n. Пусть предмет С наблюдается глазом (см. рис.1).
Рис.1
Нас интересует вопрос: на каком расстоянии h' от верхней поверхности пластинки получается изображение точки С?Для решения этого вопроса предположим, что из точки С выходят два луча, угол
Имеем,
откуда
Поэтому
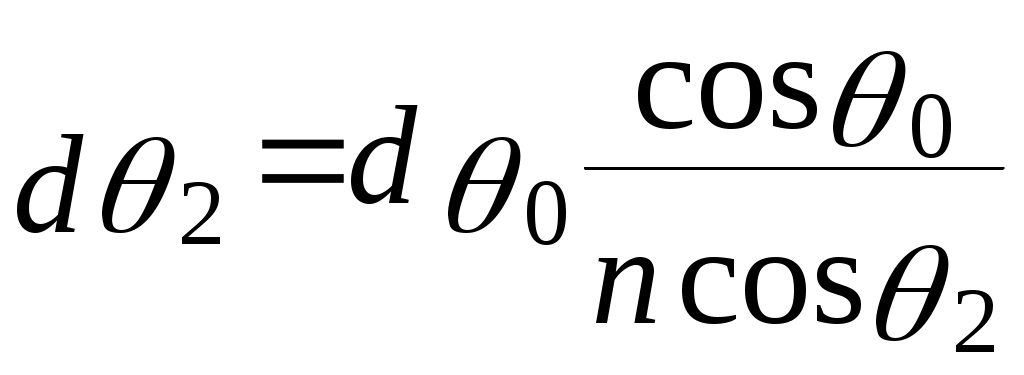
Для нахождения h` заметим, что
АВ = h
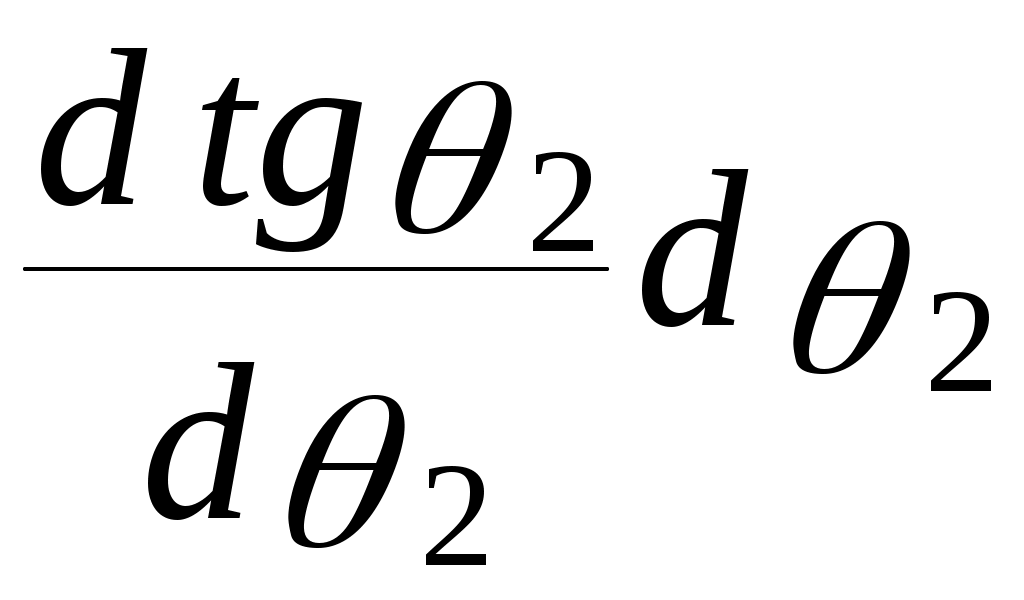
(1)
С другой стороны
АВ= h`
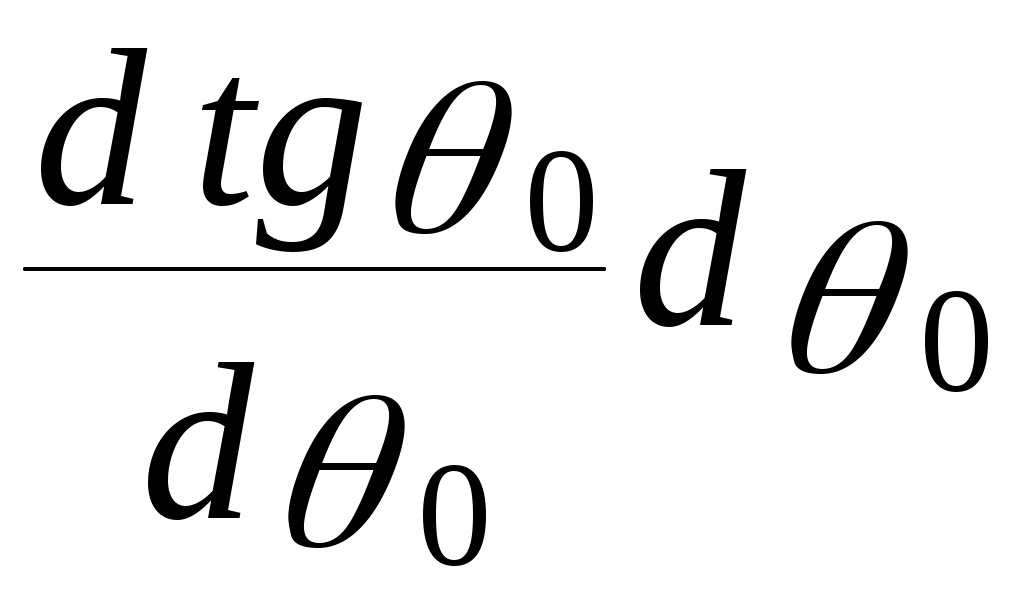 (2)
(2)Поэтому сравнивая (1) и (2), получим:
h` =
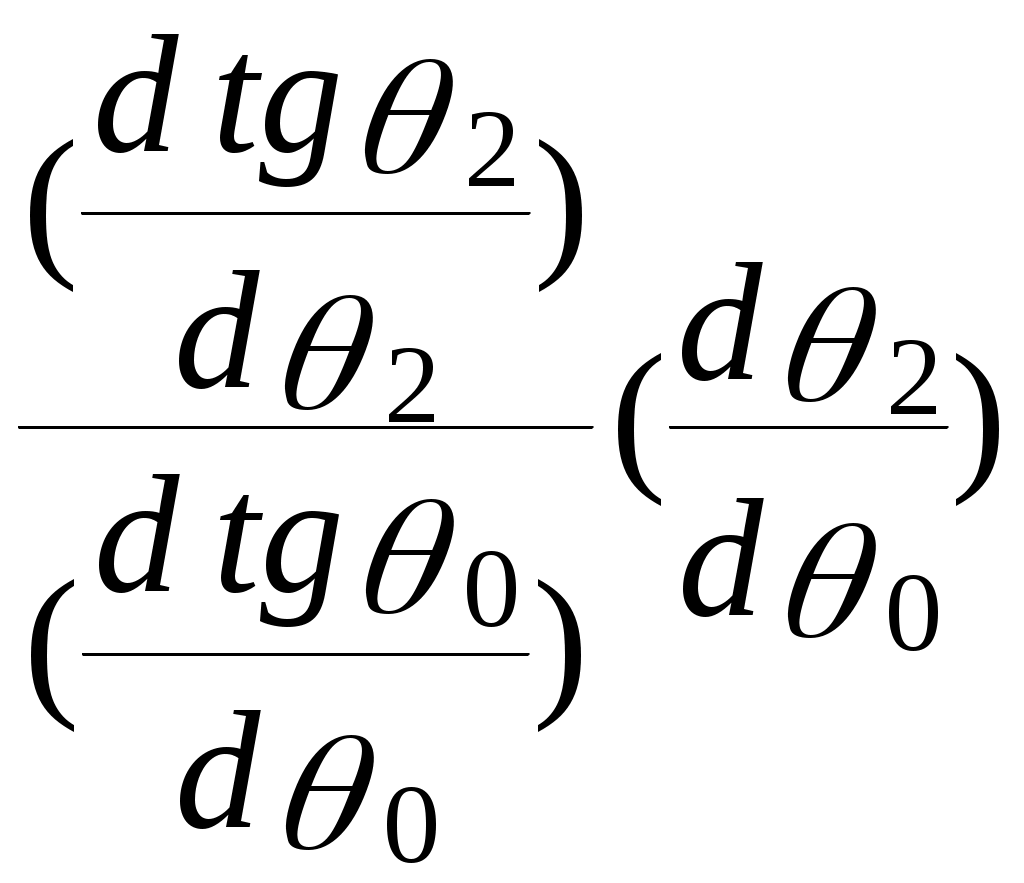 h =
h = 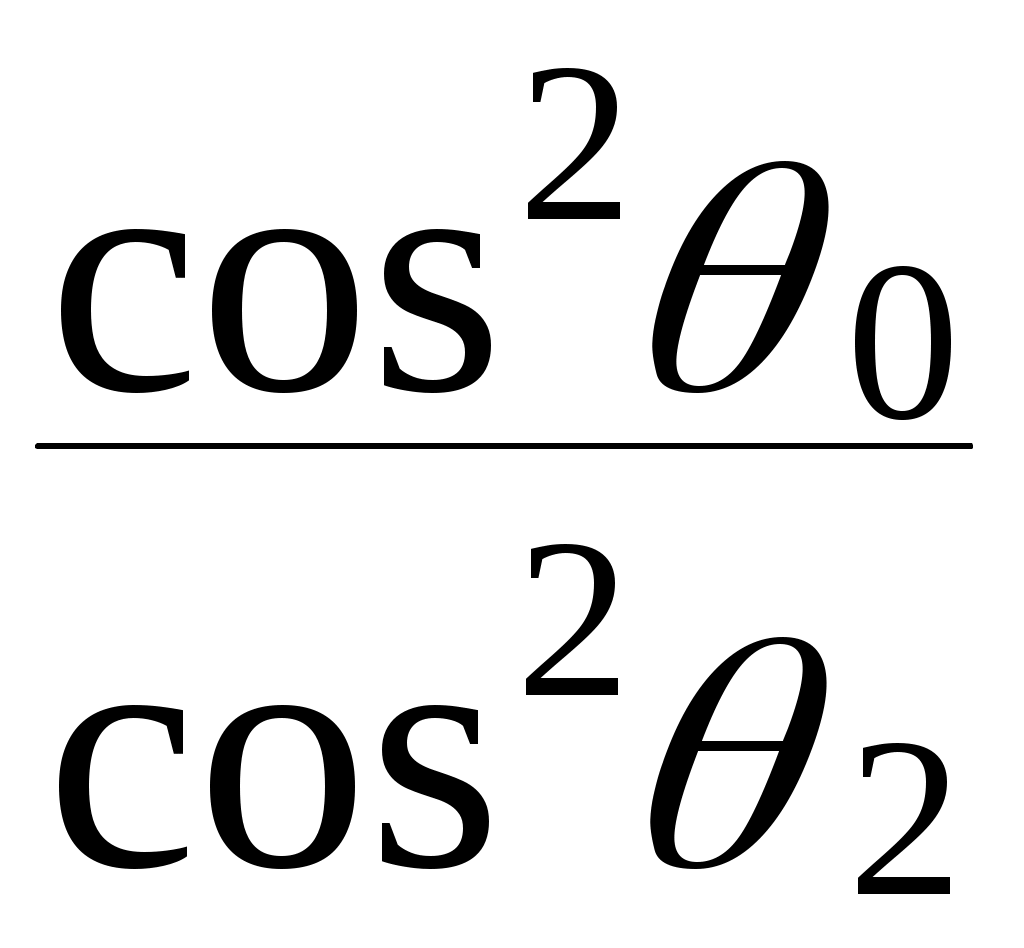 h
h 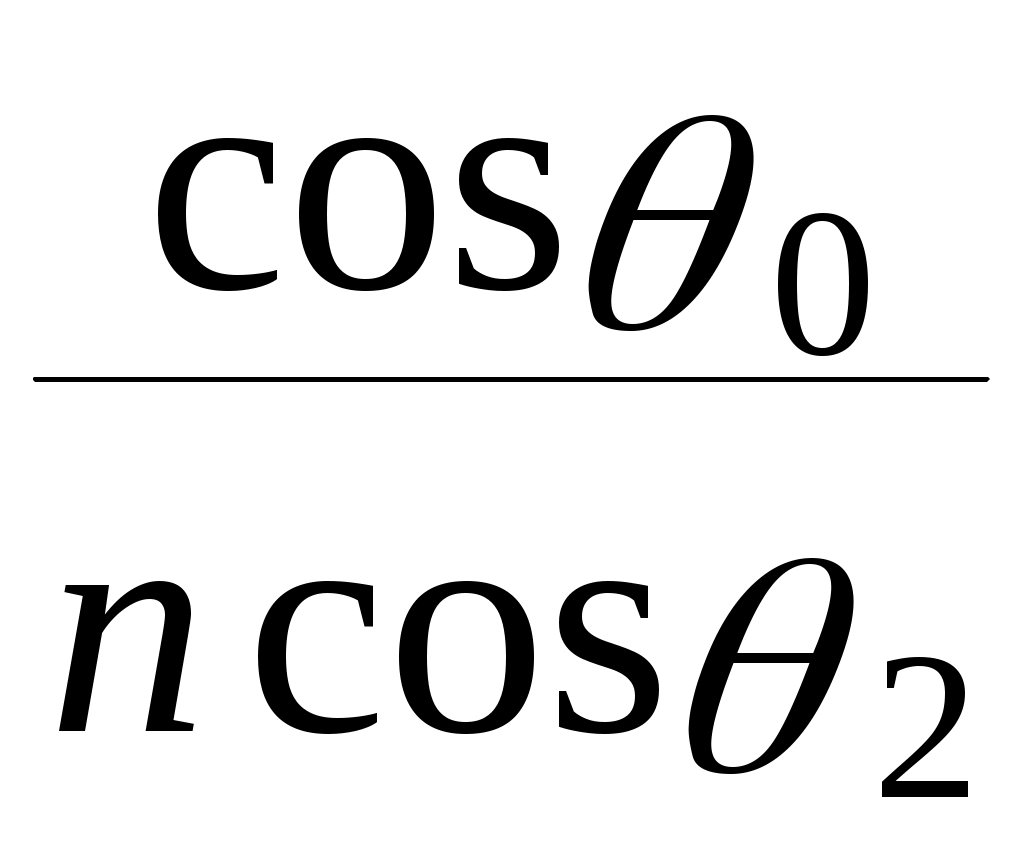 = h
= h 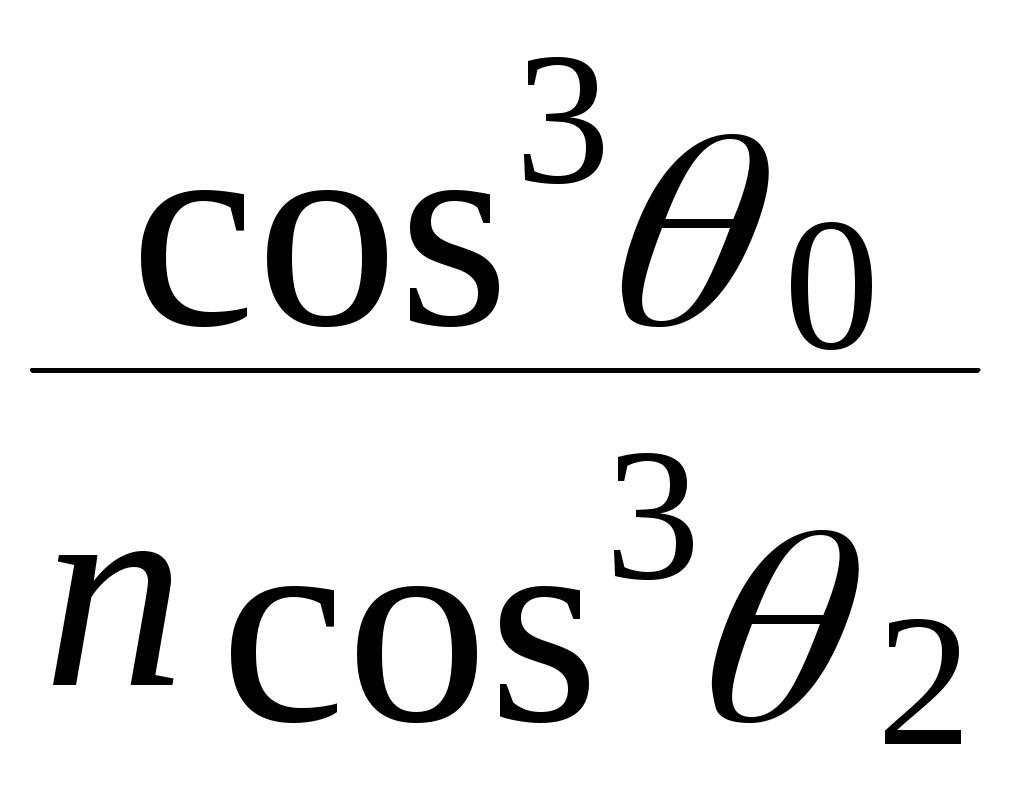 (3)
(3)Выражая
h` = h
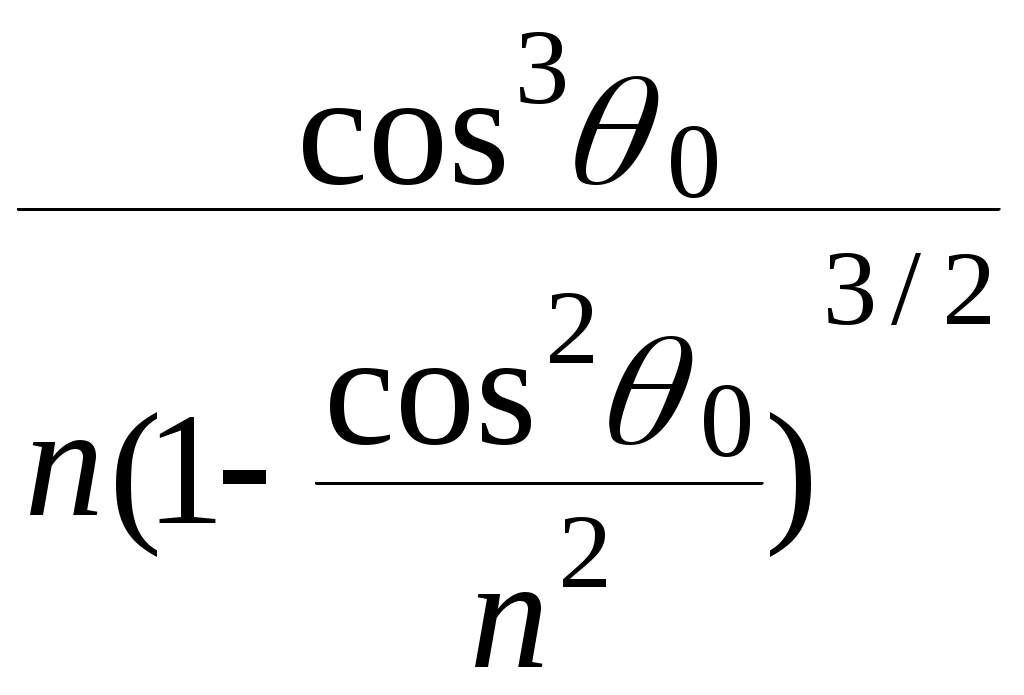 . (4)
. (4)Для частного случая
2. Описание установки
В
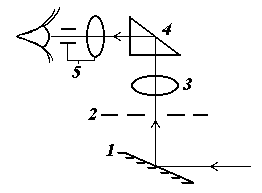
работе для определения показателя преломления стекла используется микроскоп. Оптическая схема прибора показана на рис.2. Осветительная часть состоит из зеркала (1), а наблюдательная включает в себя предметный столик (2), куда помещается исследуемый объект, объектив (3), призму (4) и окуляр (5).
Рис.2. Оптическая схема микроскопа
-
Порядок выполнения работы. .
Для измерений используются две плоскопараллельные пластинки (стекло и оргстекло) с разными толщинами.
3.1. С помощью штангенциркуля измерить их толщины
3.2. Определить средние значения истинных толщин пластинок
3.3. Поместить пластинку на предметный столик. Поднять тубус микроскопа с помощью микрометрического диска, вращая его против часовой стрелки до упора. С помощью ручек грубой фокусировки получить четкое изображение верхнего следа.
3.4. Вращая диск микрометрической фокусировки против часовой стрелки, получить четкое изображение нижнего следа.
3.5. Определить видимую толщину пластинки
3.6. Повторить пп.3.3. – 3.5. пять раз для обеих пластинок.
3.7. Определить средние значения видимых толщин пластинок
3.8. По формуле
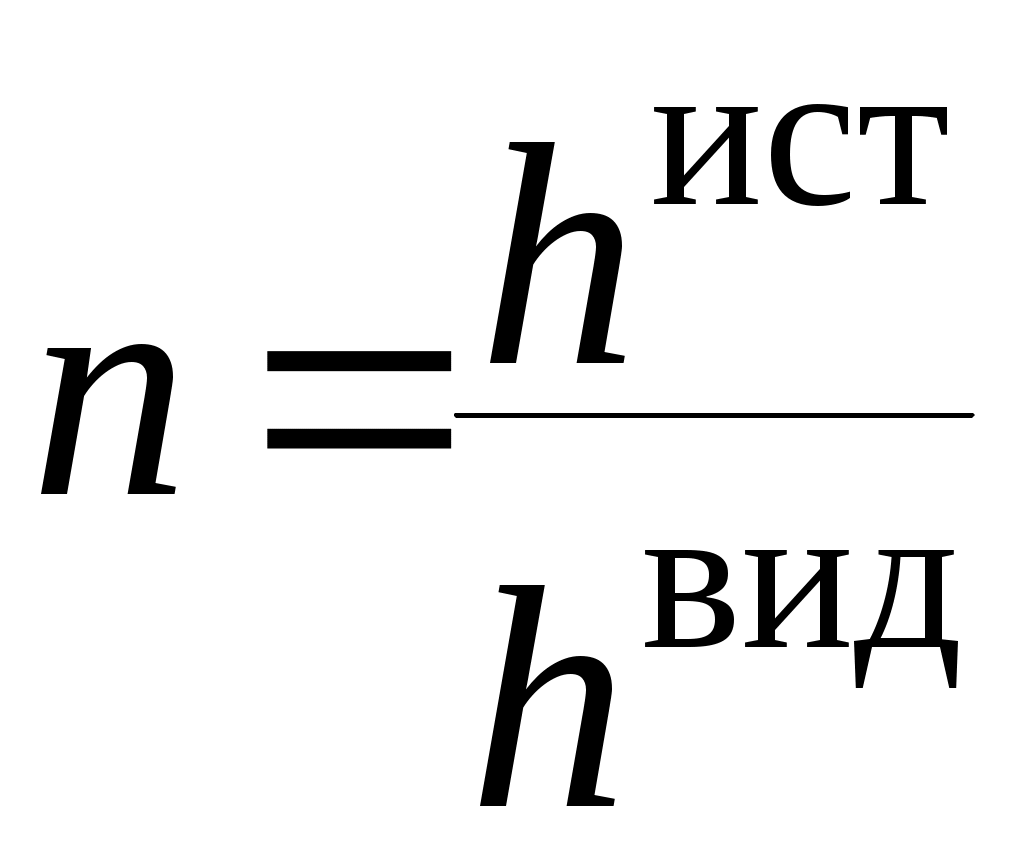 найти коэффициент преломления стекла.
найти коэффициент преломления стекла.3.9. Вычислить доверительный интервал значений
3.10. Занести результаты в таблицу 1.
Таблица 1. Истинные и видимые толщины пластинок
| материал пластинки | истин-ная толщи-на плас-тинки мм | сред-нее значе-ние | средне-квадра-тичное откло-нение | видимая толщина плас-тинки | среднее значение | средне-квадра-тичное откло-нение мм | коэффи-циент прелом-ления n | средне-квадра-тичное откло-нение мм | довери-тельный интер-вал % |
| стекло | | | | | | | | | |
| | | ||||||||
| | | ||||||||
| | | ||||||||
| | | ||||||||
| оргстекло | | | | | | | | | |
| | | ||||||||
| | | ||||||||
| | | ||||||||
| | |
4. Контрольные вопросы и задания
1. Для какой формы границы раздела двух сред справедлив закон Снеллиуса для плоской волны?
2. Можно ли пользоваться законом преломления Снеллиуса для световой волны, падающей из воздуха на границу диэлектрического шара с показателем преломления n = 1.5 и радиусом R = 10 см.
3. На дне сосуда, наполненного водой до высоты h, находится точечный источник света. На поверхности воды плавает круглый диск так, что его центр находится над источником. При каком минимальном радиусе диска лучи от источника не будут выходить из воды?
4

. На шар радиуса R, изготовленный из материала с меньшим показателем преломления, чем показатель преломления среды, где находится шар, падает пучок параллельных лучей. Определить радиус светового пучка, который может проникнуть в шар.
5. Стеклянная пластинка, показатель преломления которой n, находится в воздухе. Могут ли лучи, падающие на грань 1, после преломления на ней испытать полное внутреннее отражение на грани 2?
6. То же, что и в п.5, но в случае, когда грань и пластинки граничит с жидкостью с показателем преломления n3>1.
7. То же, что и в п.5, только вместо жидкости помещается плазма с показателем преломления n3<1.
8. Что такое мнимое изображение? Когда оно получается и трактуется?
9. К зеркалу подносится фотопластинка. Будет ли на фотопластинке запечатлено изображение предмета, находящегося перед зеркалом?
10. Как объясняется явление миража?
11. Объяснить причину искривления солнечных лучей в атмосфере Земли. К чему приводит такое искривление? (Рассмотреть восход и заход Солнца).
12. Какие еще методы (кроме описанного в данной работе) вы можете предложить для определения показателя преломления?
13. Доказать, что если световой луч проходит несколько сред разделенных плоскопараллельными границами, то направление выходящего луча зависит только от направления входящего луча и от показателей преломления первой и последней сред.
14. Под стеклянной пластинкой толщины d=15 см лежит маленькая крупинка. На каком расстоянии l от верхней поверхности пластинки образуется ее видимое изображение, если луч зрения перпендикулярен к поверхности пластинки, а показатель преломления стекла n = 1.5?
