Строки транспортной таблицы соответствуют ПО (в последней клетки каждой строки указан объем запаса груза), а столбцы – ПН (последняя клетка каждого столбца содержит значение потребности. Все клетки таблицы (кроме тех, которые расположены в нижней строке и в правом столбце) содержат информацию о перевозках x_ij и их стоимости с_ij.

Запишем систему ограничений.

1) Ограничение по уровню запасов: Суммарное количество груза, направленного из каждого ПО во все ПН должно быть равно запасу груза в данном ПО:



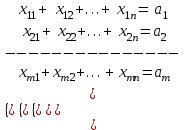
2) Ограничение по уровню спроса: Суммарное количество груза, доставляемого в каждый ПН из всех ПО должно быть равно заявке данного ПН:



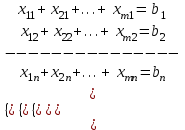
Целевая функция: Суммарная стоимость всех перевозок, которую необходимо минимизировать:



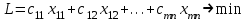
Планом перевозок называется любая совокупность значений переменных x_ij - матрица размера m×n.

Допустимым решением называется план x_ij, удовлетворяющий системе ограничений ТЗ.

Оптимальным решением называется допустимое решение, доставляющее минимум целевой функции.

Решение ТЗ в Excel

Надстройка Поиск решения в Microsoft Excel позволяет напрямую находить оптимальное решение транспортной задачи.

I. Закрытая модель, .

До вызова Поиск решения необходимо подготовить данные для решения ТЗ на рабочем листе Excel.

В Excel закрытая задача решается учетом ограничений для всех отправителей и всех потребителей

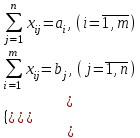- условия полного распределения запасов и полного удовлетворения потребностей.

Пример 8. На трех складах имеется мука в количестве 60, 130, 90 т., которая должна быть доставлена четырем хлебозаводам в количестве 30, 80, 60, 110 т соответственно. Составить оптимальный план перевозок

---

, имеющий минимальные транспортные расходы, если стоимость доставки 1 т муки на хлебозаводы задана матрицей



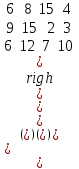
▼ Рабочий лист Excel имеет вид

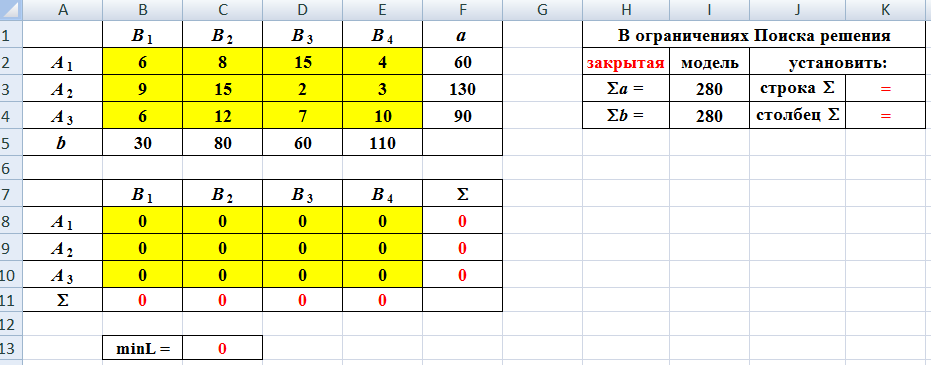
Приведем последовательность ввода данных задачи и формул в соответствующие ячейки.

A1:F5 — вводится транспортная таблица примера.

I3 — вычисляется сумма по строкам по формуле =СУММ(F2:F4).

I4 — вычисляется сумма по столбцам по формуле =СУММ(B5:E5).

Из сравнения значений делается сообщение о типе модели (закрытая, открытая) и типе ограничений (=, < =) в окне Поиск решения.

A7:F11 — составляется начальная матрица перевозок (вначале копируется транспортная таблица, затем редактируется)

В8:Е10 — производится резервирование и обнуление изменяемых переменных (начальная матрица перевозок).

F8:F10 и B11:E11 — подсчитываются суммы Σ по строкам и столбцам начальной матрицы перевозок.

С13 — вычисляется стоимость начального плана L по формуле =СУММПРОИЗВ(B2:E4;B8:E10).

Далее нужно выполнить команду Поиск решения. В диалоговом окне Поиск решения:

• установить целевую ячейку L равной минимальному значению;

• в качестве изменяемых ячеек ввести матрицу перевозок x_ij;

• установить ограничение для всех отправителей и всех потребителей;

• выбрать метод решения: Поиск решения лин. задач симплекс-методом.

Заполненное диалоговое окно Поиск решения имее следующий вид

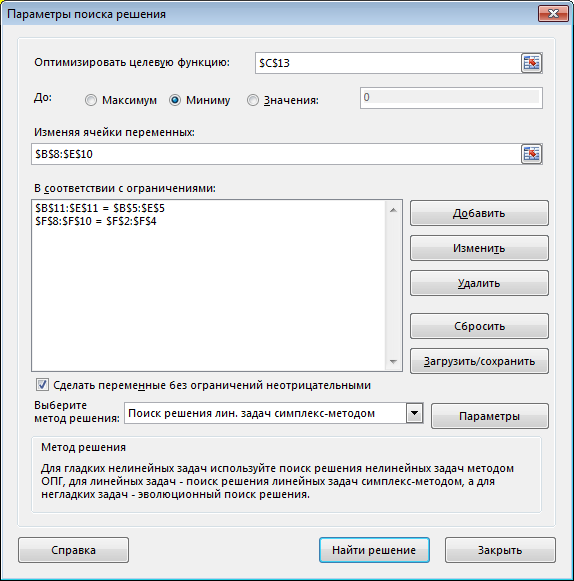
Равенство $B$11:$E$11 = $B$5:$E$5 означает условие полного удовлетворения потребностей.

Равенство $F$8:$F$10 = $F$2:$F$4 означает условие полного распределения запасов.

После выполнения программы работы «Поиск решения» получим

	B1	B2	B3	B4	
А1	0	60	0	0	60
А2	0	0	20	110	130
А3	30	20	40	0	90
	30	80	60	110
	L =	1550

---

Оптимальное решение 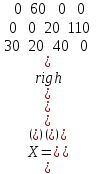, 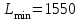усл. ед.

Таким образом, из первого склада следует отправить муку на 2-й хлебозавод в количестве 60 т., из второго склада — на 3-й и 4-й хлебозаводы в количестве 20 и 110 т. со­ответственно, из третьего склада — на 1-й, 2-й и 3-й хлебозаводы в количестве 30, 20 и 40 т. со­ответственно. При этом минимальные транспортные расходы составят 1550 усл. ед ▲

Упражнение 2. На предприятии имеются три группы станков, каждая из которых может выполнять пять операций по обработке деталей (в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 110, 130 ч. Производительность каждой группы станков на каждую операцию задана матрицей 



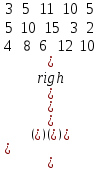
Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.

Ответ. Оптимальное решение

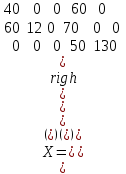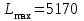, шт.

Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 ч со­ответственно, на второй группе — операции 1, 2 и 3 продолжи­тельностью 60, 120 и 70 ч соответственно, на третьей группе — операции 4 и 5 продолжительностью 50 и 130 ч соответственно. При этом максимальное число обработанных деталей составит 5170 шт.

II. Открытая модель, .

Для открытой модели может быть два случая:

a) суммарные запасы превышают суммарные потребности: ;

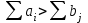b) суммарные потребности превышают суммарные запасы: .

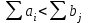В Excel открытая задача решается путем изменения ограничений по предложению (если предложение превышает спрос) или по спросу (если спрос превышает предложение), т.е. система ограничений будет иметь вид:

a)

---

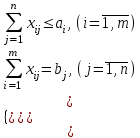
- условия неполного распределения запасов и полного удовлетворения потребностей;

b) 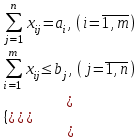- условия полного распределения запасов и неполного удовлетворения потребностей.

Пример 9. Три торговых склада могут поставлять некоторое изделие в количестве 9, 4, 8 т. Величина спроса трех магазинов розничной торговли на это изделие равна 3, 5, 6 т соответственно. Стоимости перевозок единицы груза от каждого поставщика к каждому потребителю заданы матрицей



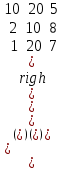
Требуется составить такой план перевозок, при котором спросы на изделия в магазины были бы выполнены при минимальной стоимости всех перевозок.

▼ Рабочий лист Excel и заполненное диалоговое окно Поиск решения имеют следующий вид



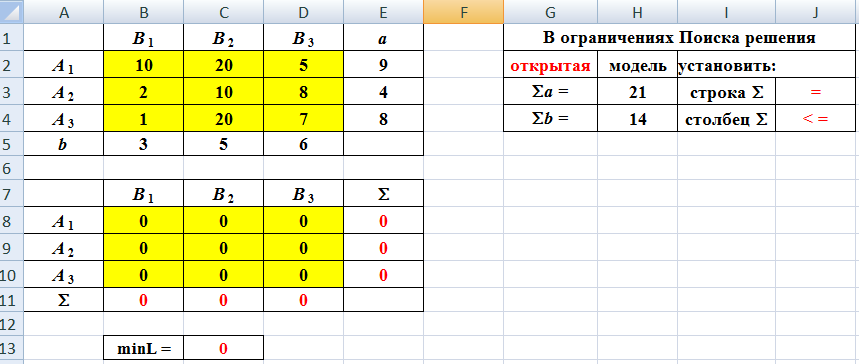
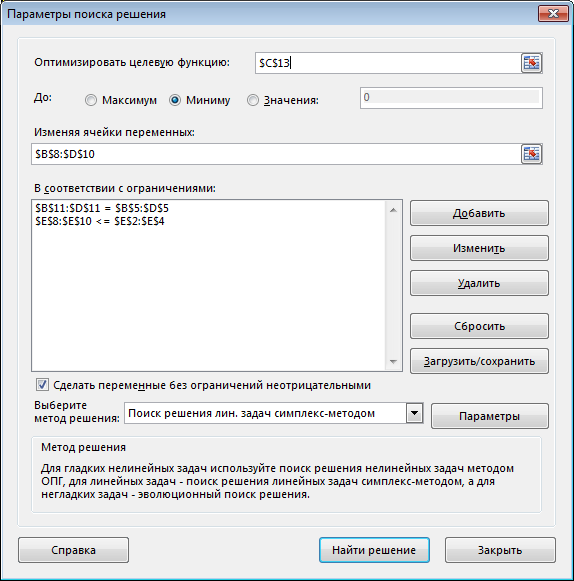
Неравенство $E$8:$E10< = $E$2:$E$4 означает условие неполного распределения запасов.

После выполнения программы работы «Поиск решения» получим

	B1	B2	B3	
А1	0	0	6	6
А2	0	4	0	4
А3	3	1	0	4
	3	5	6
	L =	93

---

Оптимальное решение , ▲

---

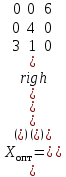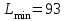Смотрите также файлы

• !Сйытар мен газдарды озалысы туралы ылымгидромеханика задарымен жылдамдыты анытайтын процестер.docx

• Материал в учебнике 17. История чисел и систем счисления.doc

• Тесты по курсу "Экономика общественного сектора" Концепция "экономического человека".docx

• Содержание Введение Глава Теоретические аспекты изучения советских комплексных систем управления качеством система сбт Понятие о сбт Принцип работы сбт введение.docx

• Учебник ответственные редакторы доктор юридических наук, профессор Ю. В. Грачева, доктор юридических наук, профессор.doc