Влияние диаметра «нулевого стержня».

С увеличением диаметра стержня осевая сила и крутящий момент, как видно из работы, возрастают, причем в большей степени осевая сила. Повышение осевой силы и крутящего момента связано с тем, что увеличиваются сила резания по всей длине режущей кромки и сила трения на направляющих вследствие роста силы резания на внутреннем участке режущей кромки сверла.

Влияние износа на режущей кромке сверла.

Как показали результаты опытов, значения осевой силы и крутящего момента по мере углубления сверла изменялись незначительно, не наблюдалось и значительной разницы между силами в начале и в конце сверления. Для иллюстрации сказанного на рисунке 10а показаны зависимости сил от глубины сверления при сверлении одной заготовки. Не отмечалось также увеличения сил после сверления 6 деталей (рисунок 10б). Величина фаски и износа по задней грани при этом не превышала 0,2 мм. Это дает основание предполагать, что износ режущей кромки сверла в указанном пределе не влияет на силы при глубоком сверлении. Так как от сил резания зависит нагрузка на направляющие сверла, то при данном износе режущей кромки не имело место и увеличение сил трения на направляющих. Этим и объясняется отсутствие заметного роста сил при глубоком сверлении. На основании проведенных в работе опытов по влиянию износа на силы резания можно утверждать, что наблюдаемые колебания сил по длине сверления связаны только с процессом схватывания на направляющих сверла, а не износом режущей кромки. Износ на направляющих сверла, когда длина их была равна 5 мм, а не износ по режущей кромке приводит к увеличению сил с ростом количества просверливаемых заготовок (рисунок 10). На это также не обращалось внимания. Увеличение сил по длине отверстия или после сверления нескольких заготовок связывали только с влиянием износа на режущих кромках сверла. Так М.А. Царенко [20] отмечает, что с увеличением суммарной глубины обработанных отверстий происходит затупление инструмента и при величине фаски износа по задней грани, равной 0,4 мм крутящий момент возрастает в 1,4 раза. При этом совершенно не упоминается, что увеличение момента может быть вызвано износом направляющих. Такое ошибочное представление о причинах изменения сил приводит к тому, что при сверлении переточку производят только по режущей кромке и не уделяют внимания состоянию направляющих сверла.

---

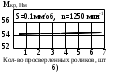
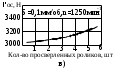
Рисунок 16–Изменение сил в зависимости от: а) глубины сверления одной

заготовки, б) количества просверленных заготовок

1.4 Анализ теоретических исследований моделей контакта при трении
Установлено, что вследствие волнистости и шероховатости поверхностей касание двух твердых тел всегда дискретно, то есть происходит в отдельных точках. В точках касания развиваются высокие удельные давления, приводящие к взаимному внедрению поверхностей на разную глубину [55, 62]. В зависимости от глубины внедрения характер нарушения фрикционных связей принято классифицировать как упругое оттеснение, пластическое оттеснение, микрорезание. Если известно распределение неровностей по высоте и величине сближения, то можно определить, какое число неровностей на какую глубину проникает. Диаметр единичного пятна касания поверхностей мало изменяется от нагрузки, поэтому кривая распределения неровностей по высоте может одновременно служить и для оценки величины площади касания. Величина фактической площади касания определяет силу трения, так как сила трения равна произведению удельной силы трения на фактическую площадь касания.

Износ с точностью до множителя l/n (где n- число циклов повторных воздействий на единичную фрикционную связь, приводящее к разрушению материала) также зависит от фактической площади касания. Поэтому вопрос об определении сближения и фактической площади касания является весьма важным для анализа процессов трения и износа. Впервые задача о сближении двух идеально гладких тел, имеющих криволинейные очертания, была рассмотрена Герцем [62]. Герц установил, что размеры и форма зоны контакта зависят от упругой деформации тел. Для двух сфер радиусами R1 и R2 центрально сжатых вместе силой 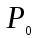(рис. 22) радиус окружности контакта задаётся зависимостью:

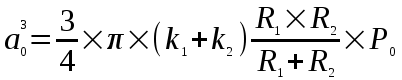, (1.1)

где 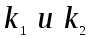- упругие константы материала каждой сферы:

,

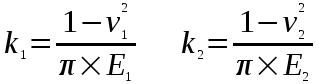где V_1, V₂ - коэффициенты Пуассона,

---

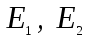
- модули упругости материала каждой сферы.

В формуле 1.1 учитывается только нагрузка Р₀ . Хотя известно, что чем больше сближение тел, тем сильнее их взаимодействие на молекулярном уровне, т.к. появляется составляющая адгезионного сцепления.

Сближение двух сферS под действием силы Ро описывается формулой

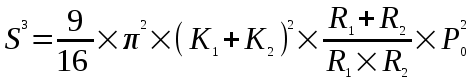(1.2)

К полученным формулам (1.16, 1.17) Герц пришел через деформирование объемов. По утверждению И.Д. Крагельского, поверхность соприкасается с деформируемым материалом (рисунок 11) по поверхности 1, в то время как при построении кривой опорной поверхности учитывается только сечение 2.


Рисунок12–Контакт двух тел с разной твердостью поверхностей


Рисунок 11–Схема контакта идеально гладких тел




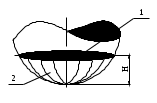
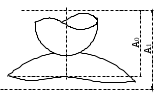
Модель Герца работает при различных диаметрах, коэффициентах Пуансона, модулях упругости и материалах сближаемых сфер. Но если контактируют два тела с различной твердостью, то контактная поверхность не окажется линейной, то есть одно тело углубится в другое (рисунок 12) и А0 будет неопределенной величиной.

Дальнейший вклад в изучение взаимодействия тел внесли Робертсон и Канделл. При небольших нагрузках ими были определены силы сцепления поверхностей, когда последние были сухими и смазанными. Эти дополнительные силы увеличивали область контакта и были особенно заметны при стремлении нагрузкиР0 к нулю, а контактная поверхность между сферами оказывается значительно больше, чем следует из формулы Герца. На рисунке 13 а штриховыми линиями показаны контактирующие сферы радиусов R1, R2, радиус контакта, рассчитанный по Герцу для нагрузки Р0 , равен а0. В действительности контакт имеет радиус а1, а сфера приобретает форму, показанную сплошными линиями. В результате адгезионного сцепления нагрузка Р1 > P0.



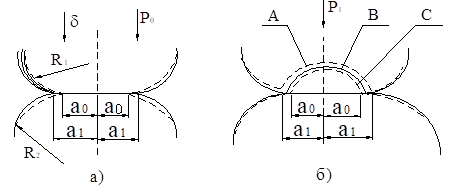
Рисунок 13–Контактирование сферических поверхностей

Распределение напряжений в зоне контакта показано на рисунок 13б. Кривые - С, А отображают напряжение сжатия для сил

---

Р0 и Р1, а кривая В – действительное распределение напряжений. В области между кривыми А и В действуют растягивающие напряжения теоретически уходящие в минус бесконечность (практически определяющиеся силами сцепления сфер).

Ни Герц, ни Робертсон с Канделлом не указывают ограничения действия моделей, а из графика видно, что при нагрузке, которая дает пятно контакта, то есть диаметр самих шариков, сближение растет медленнее, чем диаметр пятна контакта. Рост диаметра пятна контакта с ростом нагрузки должен ускоряться, а сближение замедляется (за счет постоянства объема) (рисунок 14). При их расчетах не учитывался переход от упругого взаимодействия к пластическому.



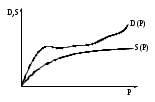
Рисунок 14–Зависимость диаметра пятна контакта D(P)

и величины сближения от нагрузки P

Упругое контактирование шероховатой поверхности моделированной в виде набора сфер с гладкой плоскостью.

Существует довольно много теоретических разработок по этому вопросу, но работа И. В. Крагельского [62] является основополагающей. Шероховатая поверхность в его работе моделируется в виде набора сферических выступов радиуса r, расположенных с постоянной плотностью (рисунок 15), закон распределения которых по высоте задается степенной функцией (1.3). При этом число выступов предполагается столь большим, что функция будет непрерывной.

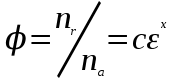, (1.3)

где 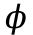- отношение числа контактирующих выступов 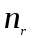к числу всех выступов поверхност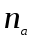и ; С и 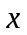- константы.

,

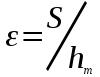где S– сближение равное деформации наиболее высокого выступа,

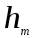- высота максимального выступа.

И.В. Крагельский [62] установил, что уравнение (1.3) при надлежащем выборе параметров С и 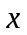хорошо описывает начальную часть кривых распределения выступов по высоте.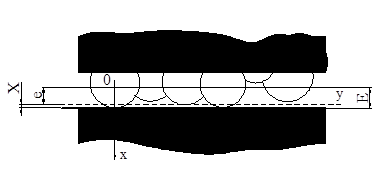



Рисунок 15–Схема контакта шероховатой поверхности с гладкой плоскостью

---

Сближение отдельного единичного выступа 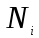может быть вычислено по формуле Герца, т.к. предполагалось, что деформируется один материал:

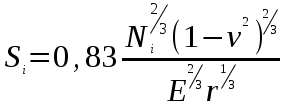, (1.4)

где: Е – модуль упругости материала;r- радиус сферы; 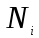- нагрузка на единичный выступ; v- коэффициент Пуассона. Тогда нагрузка, воспринимаемая единичным выступом при относительной деформации 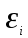, равна:

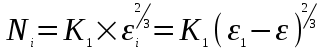, (1.5)

где 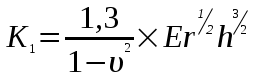max. (1.6)

Полная нагрузка, приложенная к поверхности, будет равна

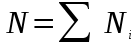
т.е. 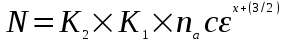(1.7)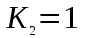

при х=0, 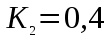при х=1, 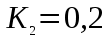при х=2.

В формуле присутствуют те же величины, что и у Герца (нагрузка, модуль упругости, радиус сферы и коэффициент Пуассона). Затем Крагельский представляет нагрузку, как функцию от hmax константами С и и - число всех выступов поверхности. И функция сближения принимает вид: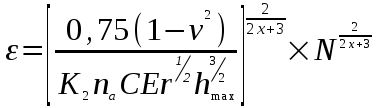

(1.8)

и 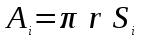, получена формула для расчёта фактической площади контакта. При рассмотрении множества сфер, как параметра, характеризующего шероховатость, автор вводит параметр W, который зависит от кривой опорной поверхности.

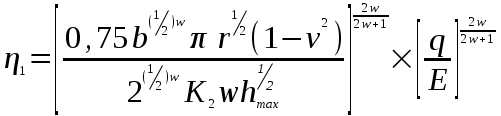(1.9)

Из формулы (1.7) видно, что фактическая площадь контакта прямо пропорциональна радиусу выступов r, удельной нагрузке qи обратно пропорциональна модулю упругости Е, максимальной высоте неровностей и параметрам, характеризующим геометрию поверхностей 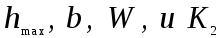. Так учитывается отношение номинального давления

---

Смотрите также файлы

• Курсовая по психологии по подготовки 44. 03. 01 образование, профилю Начальное поб17036064.docx

• Лабораторная работа 8 Получение изопропилового спирта сернокислотной гидратацией пропилена.docx

• 5 Ценностносмысловая позиция учителя.docx

• Название команды.docx

• Задание для самостоятельной работы к теме 1 Основы государственной политики в сфере воспитания. Базовые ценности российского общества.doc