Значение сцепного фактора при произвольном K_Г:

 

 

где индекс 1,0 означает что значение фактора D и D_сц соответствует K_Г = 1; G₀ - сила тяжести машины при K_Г = 0.

Семейство графиков, отражающих функциональные зависимости динамического фактора, при K_Г = 0, от скорости движения машины при всех передачах коробки перемены передач (КПП) в виде D_1,0=D(V_j), называют динамической характеристикой машины.

Семейство графиков, отражающих зависимости (2.2) и (2.3) называют нагрузочными характеристиками, соответственно, динамического и сцепного факторов. Их точки пересечения соответствуют предельным скоростным режимам, реализуемым без буксования (Р_дв=Р_сц).

Совокупность указанных характеристик - динамический паспорт машины. На рис.2.23 представлен динамический паспорт машины с механической трансмиссией имеющей КПП с четырьмя передачами I÷IV.

 



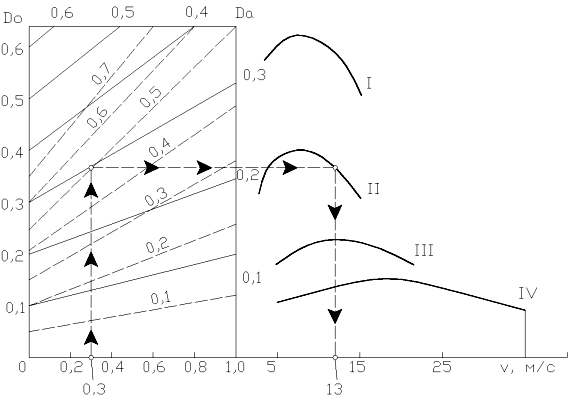
Рис. 2.23. Динамический паспорт автомобиля составляют

из динамической характеристики с номограммой нагрузок,

 графика контроля буксования и динамических показателей

 

Он даёт полную картину о возможных скоростных режимах движения машины при различных значениях степени её загрузки и позволяет оценить режимы буксования: D_сц
Так, при коэффициенте загрузки равном 0,30 возможен режим движения на II-ой передаче со скоростью 13 км/ч. При этом будет отсутствовать режим буксования, т.к.  D_сц=D.

Для СМ, являющихся технологическими, важные значения имеет свободная тяга (T₀). Под ней понимают разность между тяговым усилием и суммарным сопротивлением качению и подъему трассы, которое может быть реализовано на преодоление технологических сопротивлений при выполнении рабочих операций.

---

 

---

Основы теории рабочих процессов

 

Различают две разновидности рабочих процессов: транспортные и технологические. Последние наиболее разнообразны и определяются как характером взаимодействия рабочего органа ее средой обработки, так и характеристиками этой среды.

Несмотря на разнообразие технологий для описания реакции обрабатываемой среды на рабочий орган СМ используются ограниченное число способов (подходов).

Первый подход основан на описании изменений объекта воздействия или (среды обработки) с помощью моделей, включающих  в качестве параметров их классические физико-механические характеристики. Такой подход реализуется при изучении процессов уплотнения грунта, бурении.

Второй подход основан на использовании специальных энергетических характеристик, позволяющих через них в простой и удобной форме оценивать реакцию среды обработки на воздействие рабочего органа и движителя СМ. Простота реализации такого подхода  требует наличия значительной предварительно-полученной базы данных указанных характеристик. Этот подход реализуется в тяговых расчетах, где для описания эффекта взаимодействия СМ с поверхностью движения используются приведенные  значения коэффициентов сцепления и сопротивления передвижению. Этот же подход применяется при описании рабочих процессов:

- копания, где используются характеристики грунтов резанию и копанию;

- приготовления бетонных смесей и растворов, где используется удельный коэффициент сопротивления движению лопасти в смеси.

Третий подход не рассматривается непосредственно процесса взаимодействия дает возможность проводить оценку зон воздействия рабочего органа на среду обработки, используя для описания обычного экспотенциальные функции, в степенную часть которых закладывают физические параметры, различных видов сред. 

Примером такого подхода является оценка зоны уплотнения бетонной смеси глубинным вибратором.

 

Основы расчета привода машин

 

Целью расчета является определение энергозатрат, силовых и скоростных режимов рабочих органов и движителей в конкретных условиях работы СМ

---

 

Рассмотрим последовательно основы расчета механического и гидрообъемного привода.

Для механического привода, пренебрегая потерями в цепях управления произведём приближённую оценку энергетических, силовых и скоростных характеристик рабочего и ходового оборудования, которую может обеспечить привод СМ. Создание необходимой величины энергопотока на рабочем органе является необходимым условием реализации рабочего процесса, но недостаточным. Достаточность будет обеспечена, если структура энергопотока, подведенного к рабочему органу, будет соответствовать условиям его нагружения со стороны обрабатываемой среды. Оценка силовых и скоростных характеристик рабочего органа СМ производиться на основании внешней механической характеристики первичного двигателя, передаточных отношений I и КПД (η) всех структур СМ. Так при вращательном движении рабочего органа его угловая скорость (рад/с) и момент вращения (Нм) определяются формулами:





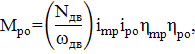
где i - безразмерная характеристика.

При линейном (поступательном) движении рабочего органа, силовая характеристика Р(Н) и скоростная V(м/с) получают по тем же формулам, с учётом того, что i в них размерная характеристика, м^-1.

Степень реальной загрузки рабочего органа СМ и, в целом всех устройств ее привода, будет определяться величинами и формами внешних силовых воздействий, воспринимаемых им со стороны среды обработки. Эти воздействия могут быть выражены в функциях координат, скоростей перемещения рабочего органа или времени. В случае их выражения через скорость перемещения рабочего органа их называют нагрузочными характеристиками. В этом случае задача нахождения требуемых режимов статического нагружения состоит в решении системы уравнений М_дв(ω) и приведенной к валу двигателя нагрузочной характеристики



Определение требуемых режимов работы производят в общем случае путем решения дифференциальных уравнений, описывающих динамические явления в системе «привод СМ-среда обработки».

---

Рассмотрим пример вращательного привода рабочего органа, реализующего технологическую операцию шлифования.

Динамические модели приводов с достаточной точностью могут быть представлены  схемами с жесткими кинематическими связями.

В этом случае эквивалентную механическую систему привода можно представить в виде одномассовой системы с массой, приведенной, например, к валу двигателя. В этом случае угол поворота двигателя α будет являться обобщенной координатой системы. Суммарный момент инерции двигателя и приведенной массы I = I_ДВ + I_пр. В переходном режиме работы привода уравнение его движения будет иметь вид:



где М_д(ω) - момент двигателя, определяемый его механической характеристикой ;

М_с(ω) - момент сил сопротивления, определяемый видом выполняемой рабочей операции и характеристиками объекта обработки;ω = dα / dt = α - скорость вращения вала двигателя;

М_дин - динамический момент, обеспечивающий изменение скорости вращения двигателя.

В установившемся статическом режиме работы (dω/dt = 0) урав­нение движения привода будет иметь вид



На основании приведенных зависимостей запишем уравнение движения привода мозаично-шлифовальной РМ с асинхронным элек­тродвигателем в статическом режиме, считая усилие прижима инстру­мента к обрабатываемой поверхности постоянным, и решим его.

В этом случае уравнение статической механической характеристи­ки двигателя имеет вид



где  ω₀ - угловая частота сети, рад/с;

S  -  скольжение ротора;S = 1 - /₀;

ν - коэффициент крутизны линеаризованной статической ха­рактеристики, соответствующий значению dM/dS при S=0; ν=S_к/(2М_К);

S_к - критическое скольжение;

М_к - критический момент,  определяемый по каталожным дан­ным.

Примем выражение для момента сил сопротивления при шлифо­вании в виде

М_с – const.

Тогда величина момента сил сопротивления, приведенная к валу двигателя:

---

Смотрите также файлы

• Viewed as an employer and wealth creator, Britains financial system is the biggest part of the British economy. Incredibly, it has overtaken industry as the countrys leading exporter (or earner of foreign currency).docx

• Контрольная работа по направлению подготовки 43. 03. 03 Гостиничное дело направленность (профиль) подготовки Гостиничная деятельность.docx

• Решение h плечо силы Ответ м о 236,94 Нм. Момент силы относительно оси.docx

• Алгоритм осмотра автотранспорта.docx

• Самодиагностика мбоу сош 1 им А. А. Курбаева с. ВольноНадеждинское в соответствии с критериями и показателями проекта Школа Минпросвещения России.docx