Добавлен: 09.01.2024
Просмотров: 102
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Саратовский государственный технический университет имени Гагарина Ю.А.»
Институт урбанистики, архитектуры и строительства Кафедра «Строительные материалы, конструкции и технологии»
САМОСТОЯТЕЛЬНАЯ РАБОТА
по дисциплине «Нелинейные задачи строительной механики»
на тему:
«Расчет нелинейно деформируемой балки»
Выполнил:
студент гр. c1-СЗС-41
Харченко Никита
Олегович
№ 190232

(дата, подпись)
Проверил:
доктор технических наук, профессор
Петров Владилен Васильевич.

(дата, подпись)
Саратов 2022 г.
Задача №1
Для нелинейно деформируемой балки с индивидуально заданными схемами закрепления и загружения распределенной нагрузкой требуется:
1. Аппроксимировать экспериментальную зависимость
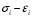 кубической параболой, параметры которой следует определить из условия прохождения кривой
кубической параболой, параметры которой следует определить из условия прохождения кривой 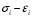 через две заданные точки на участке упрочнения материала.
через две заданные точки на участке упрочнения материала.2. Для балки с заданными условиями закрепления и нагрузкой построить аппроксимирующую функцию прогиба статическим методом В.З. Власова.
3. Используя уравнение изгиба нелинейно деформируемой балки (НДБ) в полных функциях
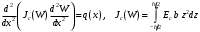
расчетать балку заданным методом.
4. Применяя аппроксимацию кривой деформирования в виде кубической параболы рассчитать балку методами:
-
Бубнова-Галеркина в полных функциях и инкрементальным методом последовательных нагружений. -
Ритца-Тимошенко в полных функциях и инкрементальным методом последовательных нагружений. -
Итерационным методом переменных параметров упругости И.А. Биргера с использованием на каждой итерации алгоритма метода Бубнова-Галеркина. -
Итерационным методом упругих решений А.А. Ильюшина с использованием на каждой итерации алгоритма метода Бубнова-Галеркина. -
Итерационным методом Ньютона-Канторовича с использованием на каждой итерации алгоритма метода Бубнова-Галеркина.
5. Результаты расчета представить в виде эпюр прогибов и изгибающих моментов. При решении задачи инкрементальными методами построить кривую «нагрузка – амплитуда прогиба».
6. Сравнить результаты расчетов (максимальные прогибы и изгибающие моменты) при заданной нагрузке, полученные всеми методами.
7. В сечении балки с наибольшим по модулю изгибающим моментом
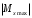 построить эпюру нормальных напряжений
построить эпюру нормальных напряжений 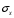 по высоте сечения.
по высоте сечения. 8. В конце работы провести анализ полученных результатов и сформулировать развернутые выводы.
Исходные данные
Параметры нелинейно деформируемой балки:
Длина
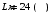
Прямоугольным поперечным сечением с высотой
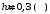 и шириной
и шириной 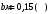
Левая опора балки — Шарнир
Правая опора балки — Заделка
Нагрузка —

Метод расчета для п.3 — Ритца-Тимошенко
Диаграмма № 3
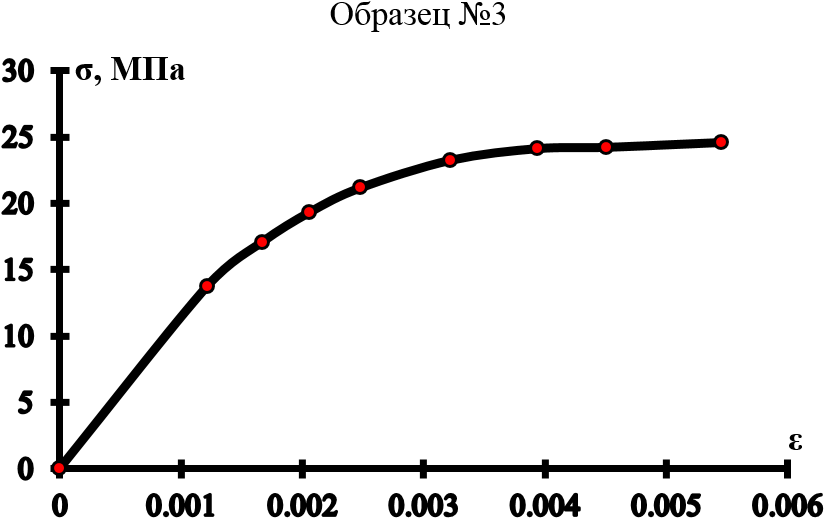
Рисунок 4 – Диаграмма деформирования образца №3
| Образец №3 | |
| ε | Σ |
| 0 | 0 |
| 0.001217 | 13.75250 |
| 0.001671 | 17.08208 |
| 0.002061 | 19.31700 |
| 0.00248 | 21.16041 |
| 0.003224 | 23.23974 |
| 0.003935 | 24.10748 |
| 0.004507 | 24.21108 |
| 0.005454 | 24.57353 |
1. Аппроксимировать экспериментальную зависимость
 кубической параболой, параметры которой следует определить из условия прохождения кривой
кубической параболой, параметры которой следует определить из условия прохождения кривой
 через две заданные точки на участке упрочнения материала.
через две заданные точки на участке упрочнения материала.Если экспериментальную диаграмму деформирования аппроксимируем кубической параболой
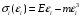 , то условия прохождения ее через точки 9 – 11 будет иметь вид
, то условия прохождения ее через точки 9 – 11 будет иметь вид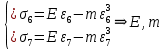
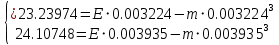
E=9418
m=2.126·108
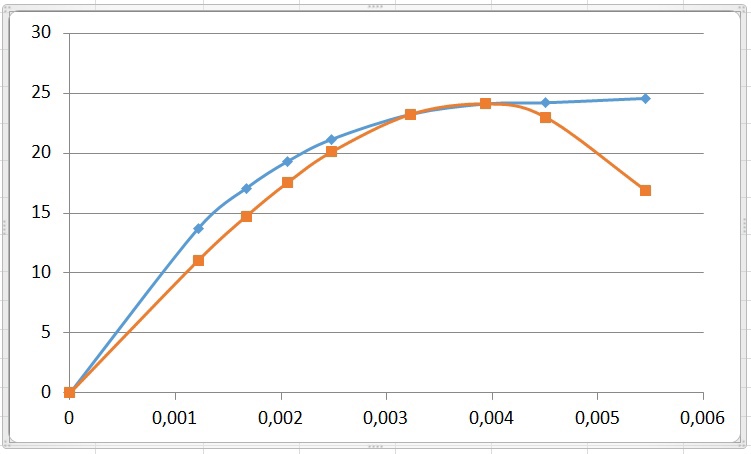
Синяя — Исходная диаграмма деформирования
Красная — Аппроксимация диаграммы в виде кубической параболы
2. Для балки с заданными условиями закрепления и нагрузкой построить аппроксимирующую функцию прогиба статическим методом В.З. Власова.
-
Определяем граничные условия:
На защемленных краях пластины должны быть равны нулю прогиб и углы наклона касательной к изогнутой срединной поверхности:
-
Жестко защемленный край: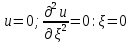
-
Жестко защемленный край: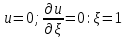
В первом приближении методом Власова прогиб пластинки будем искать в виде
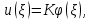
Для решения используем частный вид уравнения Софи Жермен:
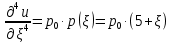
Постепенно интегрируем обе части уравнения:
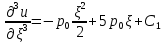
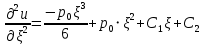
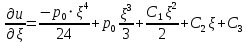
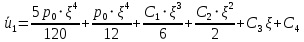
Подставляем граничные условия и определяем неизвестные константы:
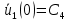 = 0;
= 0; 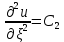 = 0
= 0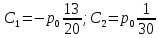
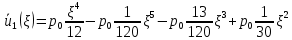
Выделяем главную часть решения, принимая
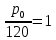 :
: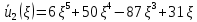
Выполняем проверку формулы прогиба балки, подставляя граничные условия:
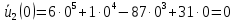
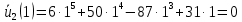
Проверка выполнена.
Рассчитаем балку методом Ритца-Тимошенко.
Выражение полной потенциальной энергии деформирования в безразмерной форме имеет вид:
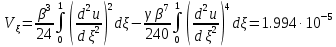
Работа внешних распределенных и сосредоточенных нагрузок в безразмерной форме подсчитывается по формуле:
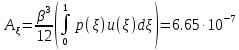 Выражение полной энергии деформируемой системы:
Выражение полной энергии деформируемой системы: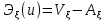
В первом приближении прогиб ищем в виде:
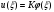
В этом случае выражение полной энергии принимает вид
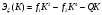 ,
,коэффициенты которого определяются по формулам
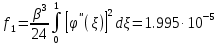
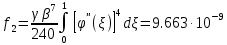
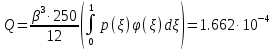
На основании теоремы Лагранжа имеем кубическое уравнение:
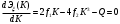 ,
,Решая которое найдем действительный корень
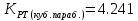
Прогиб в 1 приближении будет иметь вид:
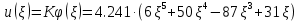
Максимальные значения прогиба и изгибающего момента:
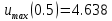
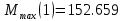
Метод Бубнова-Галеркина в полных функциях
Для расчета балки методом Бубнова-Галеркина необходимо решить обыкновенное нелинейное дифференциальное уравнение при соответствующих граничных условиях. Приближенный прогиб балки ищем в виде ряда с конечным числом членов. Аппроксимирующая функция должна быть линейно независимая, и, в отличие от метода РТ, должна удовлетворять заданным граничным условиям, как геометрическим, так и статическим.
В первом приближении обобщенная координата Kопределяется как действительный корень уравнения:
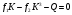 ,
,коэффициенты которого определяются по формулам:
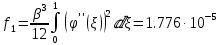
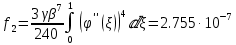
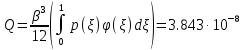
Решая которое найдем действительный корень
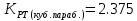
Прогиб в 1 приближении будет иметь вид:
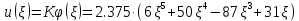
Максимальные значения прогиба и изгибающего момента:
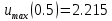
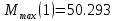
Инкрементальный метод последовательных нагружений
Бубнова-Галеркина
Для расчета балки необходимо решить линейное обыкновенное дифференциальное уравнение с известными переменными коэффициентами при заданных граничных условиях. Приращение прогиба ищем в виде ряда с конечным числом членов.
Приращение обобщенной координаты ΔKnна каждом этапе нагружения определяется по формуле: В первом приближении прогиб и приращение прогиба ищем в виде:
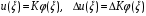
Приращение обобщенной координаты ΔKnна каждом этапе нагружения определяется по формуле:
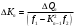
коэффициенты которого определяются по формулам:
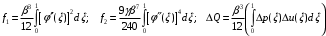
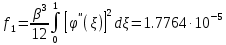
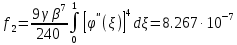
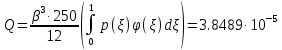
n=3;
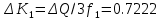
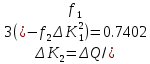
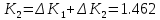
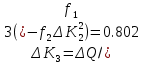
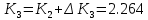
Решая линейное уравнение