Добавлен: 09.01.2024
Просмотров: 106
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, найдем действительный корень:
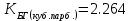
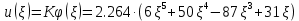
Максимальные значения прогиба и изгибающего момента:
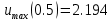
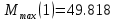
А) Выражение полной потенциальной энергии деформирования в безразмерной форме имеет вид:
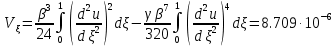
Б) Работа внешних распределенных и сосредоточенных нагрузок в безразмерной форме подсчитывается по формуле:
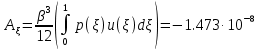 В) Выражение полной энергии деформируемой системы:
В) Выражение полной энергии деформируемой системы:

В первом приближении прогиб ищем в виде:
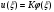
В этом случае выражение полной энергии принимает вид
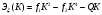 ,
,
коэффициенты которого определяются по формулам
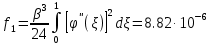
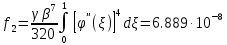
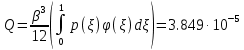
На основании теоремы Лагранжа имеем кубическое уравнение:
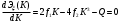 ,
,
Решая которое найдем действительный корень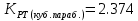
Прогиб в 1 приближении будет иметь вид:
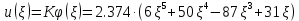
Максимальные значения прогиба и изгибающего момента:
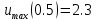
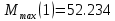
Для расчета балок методом Ритца-Тимошенко в инкрементальной форме необходимо получить выражение приращения удельной потенциальной энергии.
В первом приближении прогиб ищем в виде:
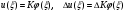
В этом случае выражение приращения полной энергии принимает вид
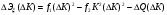
,
коэффициенты которого определяются по формулам
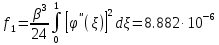
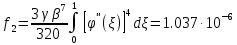
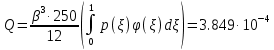
На основании теоремы Лагранжа имеем линейное уравнение:
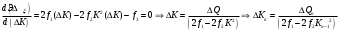
n=4;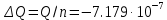
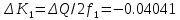
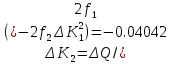
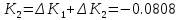
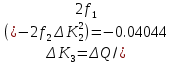
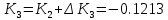
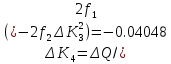
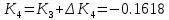
Находим амплитуду прогиба соответствующую величине заданной нагрузки
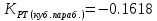
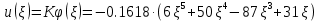
Максимальные значения прогиба и изгибающего момента:


Метод ППУ И.А. Биргера с использованием на каждой итерации алгоритма метода Бубнова-Галеркина
В соответствии с методом нелинейных параметров упругости придаем искомому прогибу в дифференциальном уравнении индекс итерации n, а прогибу в коэффициенте этого уравнения индекс n-1. В результате получаем обыкновенное линейное дифференциальное уравнение с переменными коэффициентами.
В первом приближении прогиб ищем в виде:
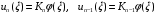
Выражение для определения обобщенной координаты Knимеет вид:
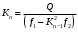 ,
,
коэффициенты которого определяются по формулам:
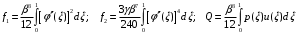
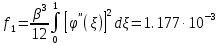
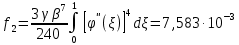
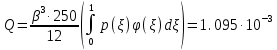
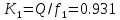
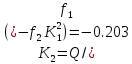
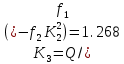
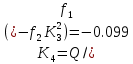
Решая линейное уравнение, при определенном количестве итераций, найдем действительный корень:
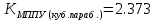
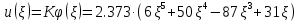
Максимальные значения прогиба и изгибающего момента:
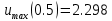
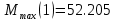
Метод УР А.А. Ильюшина с использованием на каждой итерации алгоритма метода Бубнова-Галеркина
Метод основан на возможности представления уравнения в виде линейной и нелинейной составляющих — метод начальных напряжений.
Алгоритм:
В первом приближении прогиб ищем в виде:
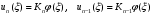
Выражение для определения обобщенной координаты Knимеет вид:
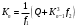 ,
,
коэффициенты которого определяются по формулам:
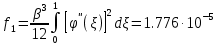
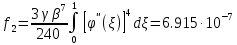
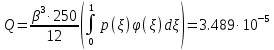
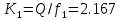
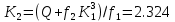
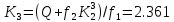
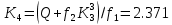
Решая линейное уравнение найдем действительный корень:
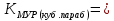
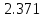
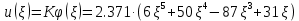
Максимальные значения прогиба и изгибающего момента:
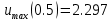
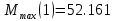
Метод Ньютона-Канторовича
Сочетание 2 методов (итерационного метода НК и инкрементального метода БГ) позволяет получить рекуррентную формулу для уточнения приближенного решения нелинейной задачи.
В первом приближении прогиб ищем в виде:
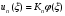
Выражение для определения обобщенной координаты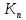 имеет вид:
имеет вид:
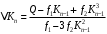 ,
,
коэффициенты которого определяются по формулам:

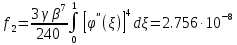
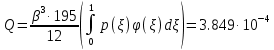
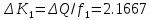
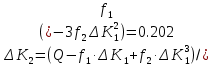
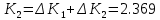
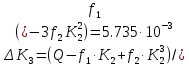
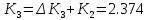
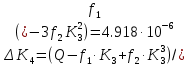
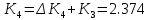
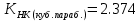

Максимальные значения прогиба и изгибающего момента:
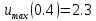

5. Результаты расчета, полученные методом Бубного-Галеркина представим в виде эпюр прогибов и изгибающих моментов.
Прогиб в 1 приближении будет иметь вид:

Построим эпюры прогиба и изгибающего момента.
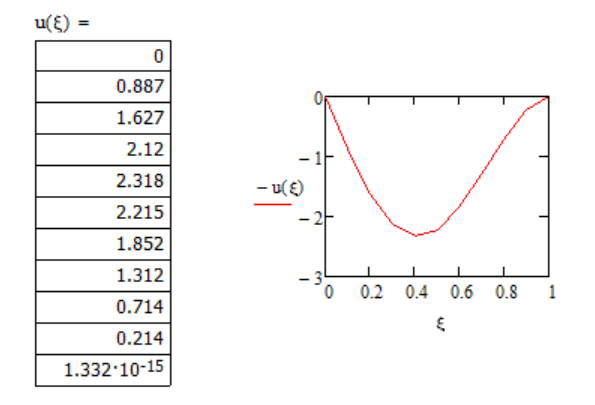
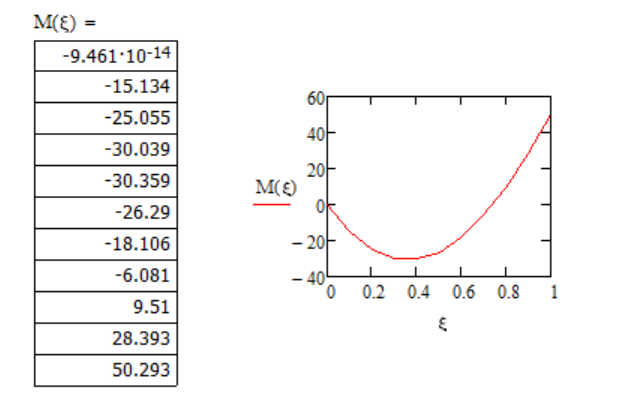
6. Сравним результаты расчетов (максимальные прогибы и изгибающие моменты) при заданной нагрузке), полученные всеми методами.
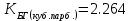
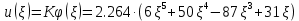
Максимальные значения прогиба и изгибающего момента:
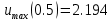
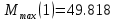
Метод Ритца-Тимошенко в полных функциях
А) Выражение полной потенциальной энергии деформирования в безразмерной форме имеет вид:
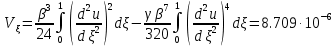
Б) Работа внешних распределенных и сосредоточенных нагрузок в безразмерной форме подсчитывается по формуле:
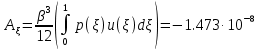 В) Выражение полной энергии деформируемой системы:
В) Выражение полной энергии деформируемой системы:
В первом приближении прогиб ищем в виде:
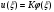
В этом случае выражение полной энергии принимает вид
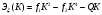 ,
,коэффициенты которого определяются по формулам
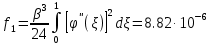
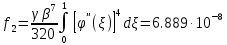
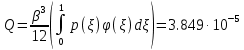
На основании теоремы Лагранжа имеем кубическое уравнение:
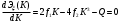 ,
,Решая которое найдем действительный корень
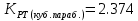
Прогиб в 1 приближении будет иметь вид:
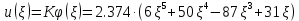
Максимальные значения прогиба и изгибающего момента:
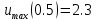
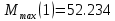
Инкрементальный метод последовательных нагружений Ритца-Тимошенко
Для расчета балок методом Ритца-Тимошенко в инкрементальной форме необходимо получить выражение приращения удельной потенциальной энергии.
В первом приближении прогиб ищем в виде:
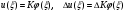
В этом случае выражение приращения полной энергии принимает вид
,
коэффициенты которого определяются по формулам
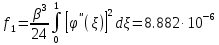
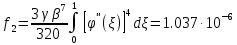
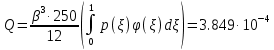
На основании теоремы Лагранжа имеем линейное уравнение:
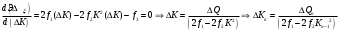
n=4;
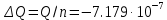
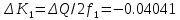
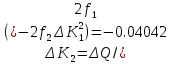
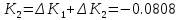
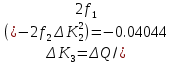
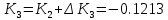
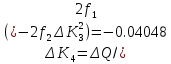
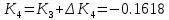
Находим амплитуду прогиба соответствующую величине заданной нагрузки
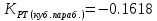
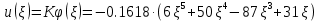
Максимальные значения прогиба и изгибающего момента:


Метод ППУ И.А. Биргера с использованием на каждой итерации алгоритма метода Бубнова-Галеркина
В соответствии с методом нелинейных параметров упругости придаем искомому прогибу в дифференциальном уравнении индекс итерации n, а прогибу в коэффициенте этого уравнения индекс n-1. В результате получаем обыкновенное линейное дифференциальное уравнение с переменными коэффициентами.
В первом приближении прогиб ищем в виде:
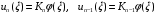
Выражение для определения обобщенной координаты Knимеет вид:
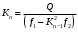 ,
,коэффициенты которого определяются по формулам:
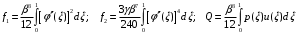
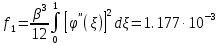
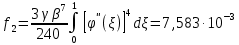
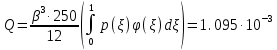
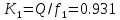
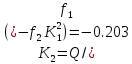
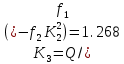
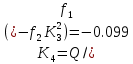
Решая линейное уравнение, при определенном количестве итераций, найдем действительный корень:
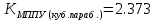
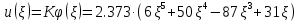
Максимальные значения прогиба и изгибающего момента:
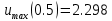
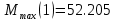
Метод УР А.А. Ильюшина с использованием на каждой итерации алгоритма метода Бубнова-Галеркина
Метод основан на возможности представления уравнения в виде линейной и нелинейной составляющих — метод начальных напряжений.
Алгоритм:
-
Для нелинейно-деформируемого материала балки выбираем подходящее аналитическое выражение диаграммы деформирования и определяем функцию пластичности ????(????) и параметр ???????? -
Для заданной нагрузки методом интегрирования ищем решение упругой задачи W1 -
С учетом найденного прогиба, получаем фиктивную нагрузку -
Решаем уравнение с фиктивной нагрузкой, находим прогиб W2 -
Определяем фиктивную нагрузку и определяем уточненное значение прогиба балки W3
В первом приближении прогиб ищем в виде:
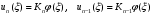
Выражение для определения обобщенной координаты Knимеет вид:
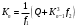 ,
,коэффициенты которого определяются по формулам:
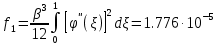
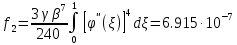
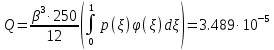
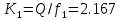
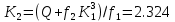
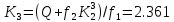
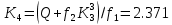
Решая линейное уравнение найдем действительный корень:
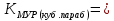
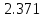
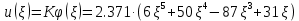
Максимальные значения прогиба и изгибающего момента:
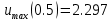
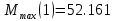
Метод Ньютона-Канторовича
Сочетание 2 методов (итерационного метода НК и инкрементального метода БГ) позволяет получить рекуррентную формулу для уточнения приближенного решения нелинейной задачи.
В первом приближении прогиб ищем в виде:
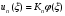
Выражение для определения обобщенной координаты
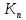 имеет вид:
имеет вид: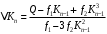 ,
,коэффициенты которого определяются по формулам:

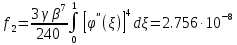
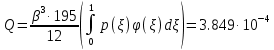
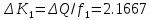
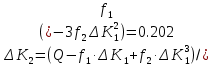
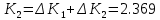
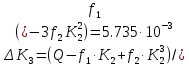
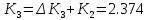
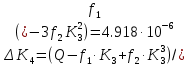
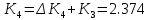
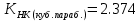

Максимальные значения прогиба и изгибающего момента:
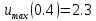

5. Результаты расчета, полученные методом Бубного-Галеркина представим в виде эпюр прогибов и изгибающих моментов.
Прогиб в 1 приближении будет иметь вид:

Построим эпюры прогиба и изгибающего момента.


6. Сравним результаты расчетов (максимальные прогибы и изгибающие моменты) при заданной нагрузке), полученные всеми методами.
| Метод расчета | 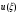 | Отклонение в % | 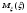 | Отклонение в % |
| Б-Г (в полных функциях) | 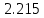 | - | 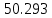 | - |
| Р-Т (в полных функциях) | 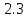 | 3.83% | 52.234 | 3.85% |
| Метод расчета | 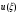 | Отклонение в % | 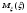 | Отклонение в % |
| Б-Г (инкремент.) | 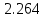 | - | 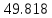 | - |
| Р-Т (инкремент.) | 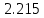 | 2.164% | 50.293 | 0.95% |
| Метод расчета | 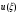 | Отклонение в % | 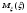 | Отклонение в % |
| МППУ И.А.Биргера | 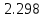 | - | 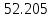 | - |
| УР А.А.Ильюшина | 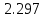 | 0.044 % | 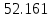 | 0.087 % |
| Н-К | 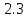 | 0.087 % | 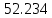 | 0.056 % |