Вариант 9.

1.Найдите производную f’(x) если:

а) 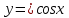б)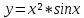

2.Найдите тангенс угла наклона касательной к графику функций:

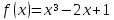в точке с абсциссой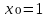

3.Напишите уравнение касательной к графику функции:

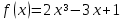в точке абсциссой x₀=1

4.Решить задачу:

Изменение силы тока I в зависимости от времени t дано уравнением

I = 2t²-5t (I - в амперах, t - в секундах)

Найдите скорость изменения силы тока в конце 10-й секунды.

5.Найти промежутки монотонности функции



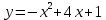
6.Найти точки экстремума функции



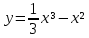
7.Найти наибольшее и наименьшее значение функции

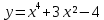
x

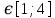
8.Найти точки перегиба, промежутки выпуклости кривой



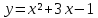
Вариант 10.

1.Найдите производную f’(x) если:

а) 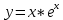б)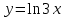

2.Найдите тангенс угла наклона касательной к графику функций:

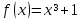в точке с абсциссой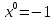

3.Напишите уравнение касательной к графику функции:

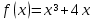в точке абсциссой x₀=2

4.Решить задачу:

Тело движется прямолинейно по закону

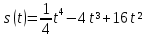
(s - метрах, t - в секундах).

Определите, в какие моменты времени тело было в начальном пункте.

5.Найти промежутки монотонности функции



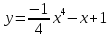
6.Найти точки экстремума функции



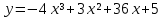
7.Найти наибольшее и наименьшее значение функции

---

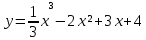
x

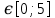
8.Найти точки перегиба, промежутки выпуклости кривой



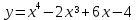
а. Время на выполнение: 90 мин.

б. Перечень объектов контроля и оценки

Наименование объектов контроля и оценки	Основные показатели оценки результата	Оценка
З 1. Основные понятия и методы математического анализа, линейной алгебры, элементарной теории вероятностей, теории комплексных чисел.	-Соответствие применения математических формул и свойств; -Способность делать обобщения и формулировать выводы; - Аргументированность применения правил дифференцирования и интегрирования основных элементарных функций;

6.1.6. Практическое задание.

а) Инструкция к заданию: Используйте правила дифференцирования сложной функции, таблицу дифференцирования.

№ Варианта	Найти производные	№ варианта	Найти производные
1	а) 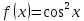б) 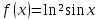в) 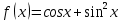г) 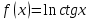д)	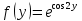12	а) 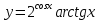б) 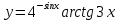в) 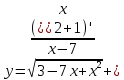г) 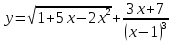д)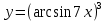
2	а) 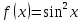б) 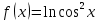в) 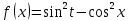г) 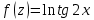д)	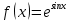13	а) 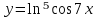б) 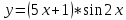в) 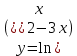г) 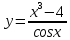д)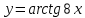
3	а) 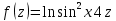б) 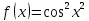в) 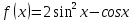г) 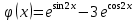д)	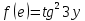14	а) 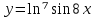б) 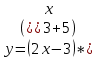в) 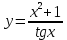г) 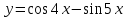д)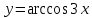
4	а) 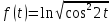б) 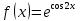в) 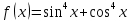г) 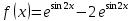д)	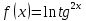15	а) 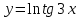б) 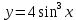в) 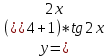г) 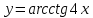д)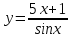
5	а) 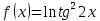б) 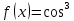в) 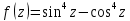г) 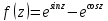д)	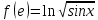16	а) 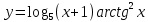б) 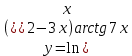в) 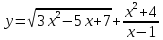г) 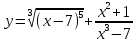д)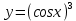
6	а) 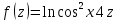б) 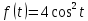в) 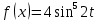г) 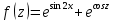д)	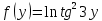17	а) 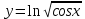б) 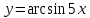в) 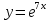г) 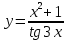д)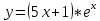
7	а) 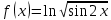б) 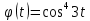в) 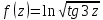г) 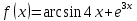д)	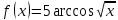18	а) 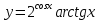б) 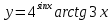в) 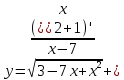г) 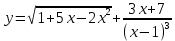д)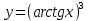
8	а) 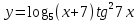б) 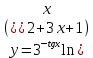в) 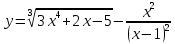г) 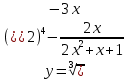д)	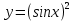19	а) 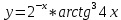б) 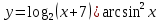в) 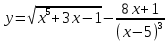г) 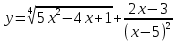д)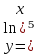
9	а) 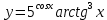б) 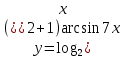в) 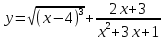г) 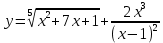д)	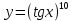20	а) 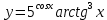б) 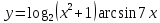в) 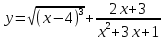г) 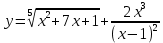д)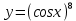
10	а) 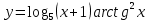б) 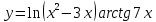в) 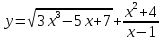г) 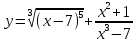д)	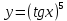21	а) 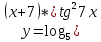б) 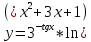в) 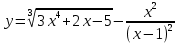г) 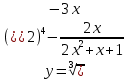д)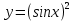
11	а) 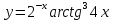б) 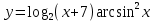в) 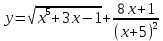г) 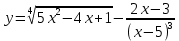д)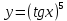

---

а. Время на выполнение: 45 мин.

б. Перечень объектов контроля и оценки

Наименование объектов контроля и оценки	Основные показатели оценки результата	Оценка
У.2. Применять простые математические модели систем и процессов в сфере профессиональной деятельности.	-Правильность выбора метода решения задач; -Аргументированность применения материала для решения экономических задач; -Полнота решения задач; -Правильность и точность вычисления; -Скорость выполнения всех видов и этапов решения задач;

6.1.7. Практическое задание.

а) Инструкция к заданию: Используя свойства интегралов, различные методы интегрирования, найти интегралы.

№ Найти интеграл
МЕТОД ТАБЛИЧНЫЙ		МЕТОД ПОДСТАНОВКИ	ОПРЕДЕЛЕННЫЙ МЕТОД
1	1 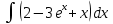2 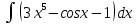3 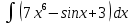4 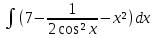5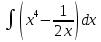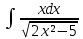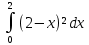
2	1 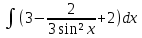2 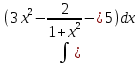3 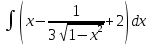4 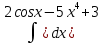5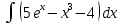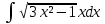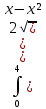
3	1 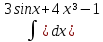2 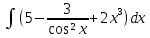3 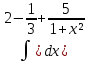4 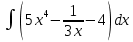5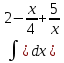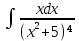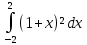
4	1 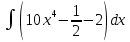2 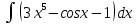3 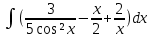4 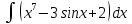5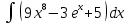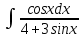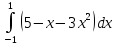
5	1 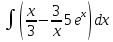2 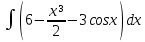3 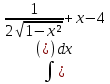4 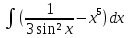5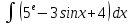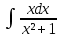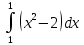
6	1 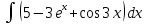2 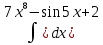3 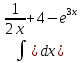4 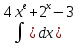5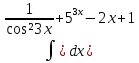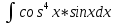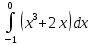
7	1 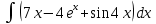2 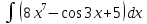3 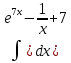4 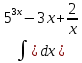5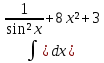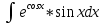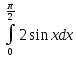
8	1 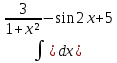2 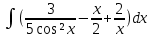3 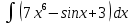4 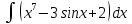5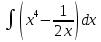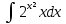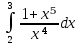
9	1 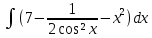2 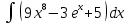3 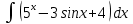4 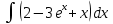5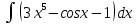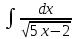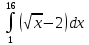
10	1 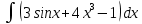2 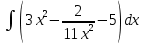3 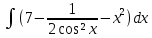4 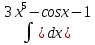5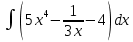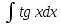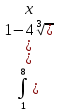
11	1 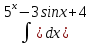2 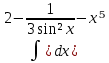3 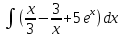4 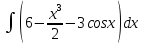5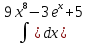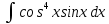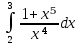
12	1 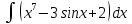2 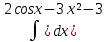3 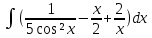4 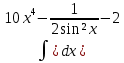5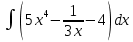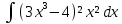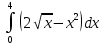
13	1 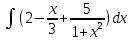2 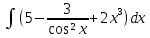3 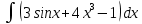4 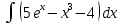5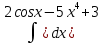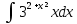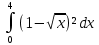
14	1 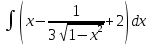2 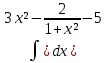3 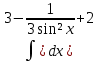4 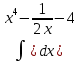5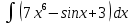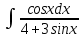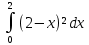
15	1 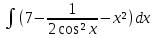2 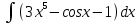3 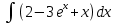4 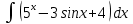5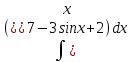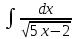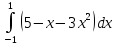

---

---

а. Время на выполнение: 45 мин.

б. Перечень объектов контроля и оценки

	Наименование объектов контроля и оценки	Основные показатели оценки результата	Оценка
У.2. Применять простые математические модели систем и процессов в сфере профессиональной деятельности.		-Правильность выбора метода решения задач; -Аргументированность применения материала для решения экономических задач; -Полнота решения задач; -Правильность и точность вычисления; -Скорость выполнения всех видов и этапов решения задач;

6.2. Раздел 2: Метод математических моделей.

6.2.1. Расчетное задание.

а) Инструкция к заданию: Используя свойства матриц и систем линейных уравнений, решить системы уравнений методом Крамера, методом Гаусса ,методом обратной матрицы.

Вариант 1

1. 
   Найти матрицу C=A+3B, если , .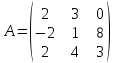
   
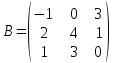2. 
   Решить систему линейных уравнений методом обратной матрицы.
   
3. 
   Решить систему линейных уравнений по формулам Крамера.
   
4. 
   Решить систему линейных уравнений методом Гаусса.
   

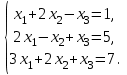
Вариант 2

1. 
   Найти матрицу C=2A-B, если , .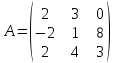
   
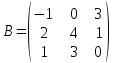2. 
   Решить систему линейных уравнений методом обратной матрицы.
   
3. 
   Решить систему линейных уравнений по формулам Крамера.
   
4. 
   Решить систему линейных уравнений методом Гаусса.
   

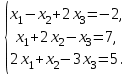
Вариант 3

1. 
   Найти матрицу C=3A+B, если , .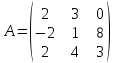
   
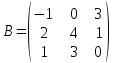2. 
   Решить систему линейных уравнений методом обратной матрицы.
   
3. 
   Решить систему линейных уравнений по формулам Крамера.
   
4. 
   Решить систему линейных уравнений методом Гаусса.
   

---

Смотрите также файлы

• Сценарий спектакля Клятва Тимура.docx

• Практических заданий по дисциплине управление проектами.docx

• Мой идеал врача.docx

• Наименование товара.docx

• Тенденции в Историографии Средневековых Скандинавских Государств (до 1350 года).docx