Файл: Программа уровень общего образования основное общее образование.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.01.2024

Просмотров: 54

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Выражения. Тождества. Уравнения.

Функции

Степень с натуральным показателем

Многочлены

Формулы сокращённого умножения

Системы линейных уравнений

Повторение. Контрольная работа.



Произведение

одночлена и многочлена
6
https://resh.edu.

ru/subject/16/7/







Самостоятельная работа
1
https://resh.edu.

ru/subject/16/7/







Произведение

многочленов
6
https://resh.edu.

ru/subject/16/7/







Контрольная работа № 5
1
https://resh.edu.

ru/subject/16/7/




Глава V. Формулы сокращённого

умножения
Квадрат суммы и квадрат разности
5
https://resh.edu. ru/subject/16/7/







Разность квадратов.

Сумма и разность кубов
5
https://resh.edu.

ru/subject/16/7/







Самостоятельная работа
1
https://resh.edu.

ru/subject/16/7/







Преобразование целых

выражений
6
https://resh.edu.

ru/subject/16/7/







Контрольная работа № 6
1
https://resh.edu.

ru/subject/16/7/




Глава VI. Системы линейных

уравнений
Линейные уравнения с двумя переменными и их системы
5
https://resh.edu. ru/subject/16/7/







Решение систем

линейных уравнений
8
https://resh.edu.

ru/subject/16/7/







Подготовка к итоговой

контрольной работе
1
https://resh.edu.

ru/subject/16/7/







Итоговая контрольная

работа
1
https://resh.edu.

ru/subject/16/7/




Повторение
Повторение
6
https://resh.edu.

ru/subject/16/7/


Приложение

Контрольно-измерительные материалы
Контрольная работа № 1 Вариант 1

  1. Найдите значение выражения 5 – 41 : 3.

  2. Вычислите значения выражений 1,8х + 0,3у и 2,6х –0,2у при х

= –2, у = 3 и сравните их.

  1. Упростите выражение: а) 7x – 3y – 9x + 8y; б) x – (6x – 1)

+ (13 – 4x); в) 5(4 – 3p) – 6(8p + 2).

  1. В палатку привезли 400 кг картофеля. В первый день продали 45% всего картофеля, а во второй — 30% остатка. Сколько картофеля осталось в палатке?

  2. Упростите выражение и найдите его значение при указанном значении переменной: а) 6(1,2а – 0,8) – 3,6а + 7,2 при а = –0,5; б) 9а – (а – (3а – 1)) при а = –1,01.

Вариант 2

  1. Найдите значение выражения 6 – 81: 7.

  2. Вычислите значения выражений 1,6а – 0,3р и 2,1а –0,1р при а

= –1, р = –2 и сравните их.

  1. Упростите выражение: а) 5a – 17b + 3b – 11a; б) 10q – (8p – 1) + (6p – 11); в) 3(2b – 6) – 0,5(12 – 4b).

  2. В книге 300 страниц. В первый день Антон прочитал 40% всей книги, а во второй — 35% остатка. Сколько стра- ниц осталось непрочитанными?

  3. Упростите выражение и найдите его значение при указанном значении переменной: а) –5(1,4а – 6) + (3,4а – 1) при а = 1; б) 10p – (3p – (p + 4)) при p = –0,1.

Контрольная работа № 2 Вариант 1

1. Решите уравнение: а) 7 х = 56; б) 17,2 – 4у = 0; в) 8,5 – 2х = 1,3 + 7х.

  1. В двух ящиках находится 56 деталей. Сколько деталей в каждом ящике, если в одном из них на 6 деталей больше, чем в другом?

  2. Найдите среднее арифметическое, размах и моду ряда чисел 29, 18, 11, 18, 6, 14.

  3. Одно из двух чисел в 4 раза больше другого. Если меньшее число уменьшить на 1, а большее увеличить на 2, то первый результат будет в 6 раз меньше второго. Найдите эти числа.

  4. В ряду чисел 6, 8, , 12, 15 пропущено одно число. Найдите его, если известно, что среднее арифметическое этого ряда равно 10.

Вариант 2

1. Решите уравнение: а) 5 х = –30; б) 1,6 – 0,08у = 0; в) 7,6 – 3х = 4,1 + 2х.

  1. В двух седьмых классах учатся 54 учащихся, причём в одном из них на 2 учащихся меньше, чем в другом. Сколько учащихся учится в каждом классе?

  2. Найдите среднее арифметическое, размах и моду ряда чисел 48, 42, 56, 48, 16, 18.

  3. Одно из двух чисел в 5 раз больше другого. Если большее число уменьшить на 2, а меньшее увеличить на 2, то первый результат будет втрое больше второго. Найдите эти числа.

  4. В ряду чисел 4, 8, 12, , 13, 7 пропущено одно число. Найдите его, если известно, что среднее арифметическое этого ряда равно 9.

Контрольная работа № 3 Вариант 1

  1. Функция задана формулой у = 3х – 9. Найдите: а) значение у, если х =– 3 ;0; 4,5; б) значение х, при котором у = –3; 0; 6.

  2. График какой из функций y = 2x + 11, y = –x + 16, y = 3x, проходит через начало координат? Постройте этот график.

  3. На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.



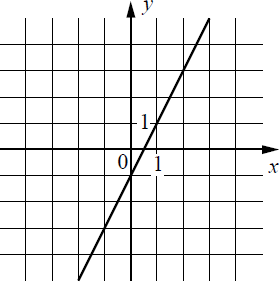
  1. Не выполняя построения, найдите координаты точек пересечения графика функции у = 0,6х – 4,2 с осями координат.

  2. Задайте формулой линейную функцию, график кото- рой проходит через точку Р(0; –3) и параллелен графику функции у = 3х – 2.

Вариант 2

  1. Функция задана формулой у = –6х + 15. Найдите: а) значение у, если х = –0,5; 0; 21; б) значение х, при котором у = –3; 0; 20.

  2. График какой из функций у = –2х + 1, у = –х, у = 6х

+ 3 проходит через начало координат? Постройте этот график.

  1. Постройте график функции у = –0,5х + 2.

  2. Не выполняя построения, найдите координаты точек пересечения графика функции у = 1,5х + 3 с осями координат.

  3. Задайте формулой линейную функцию, график кото- рой проходит через точку Р(–2; 0) и параллелен графику функции у = 1,5х + 1.

Итоговая контрольная работа Вариант 1

  1. Упростите выражение (a + 5)2 – (a + 2)(7 + a).

  2. Решите систему уравнений: 4x – y = 18, а) 3x + 5y = 2; 3x + 4y

= 17, б)4x – 5y = –29.

  1. Постройте график функции у = 2х – 3. Проходит ли этот график через точку А(9,5; 16)?

  2. Разложите на множители многочлен: а) 2a3 – 128a; б) 5a – b2

– ab + 5b.

  1. Первый участок пути протяженностью 120 км автомобиль проехал со скоростью 80 км/ч, следующие 75 км — со скоростью 50 км/ч, а последние 110 км — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Запишите решение и ответ.

  2. Решите уравнение: а) 16x – x3 = 0; б) y8 + 1 – 2y4 = 0. Вариант 2

  1. Упростите выражение (a + 4)2 – 2a(4 + 3a).

  2. Решите систему урн авнений: x – 3y = 8,а) 6x + 5y = 25; м3x + 4y

= 29, б) о4x + 7y = 52.

  1. Постройте график функции у = 2х + 3. Проходит ли этот график через точку В(7,5; 18)?

  2. Разложите на множители: а) x3 – 81xy2; б) a2 – 13b + 13a – ab.

  3. Первый участок пути протяженностью 150 км автомобиль проехал со скоростью 90 км/ч, следующие 85 км — со скоростью 50 км/ч, а последние 100 км — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Запишите решение и ответ.

  4. Решите уравнение: а) x3 – 64x = 0; б) y12 + 4 – 4y6 = 0.

Смотрите также файлы