Файл: 1. основные положения оптимизации.doc

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ОПТИМИЗАЦИИ

1.1. Оптимизация в задачах управления и проектирования

Оптимизация – это процесс нахождения наилучшего решения задачи, определяемого по некоторому заранее установленному критерию. Другими словами, это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Оптимизация в широком смысле слова находит применение в науке, технике и в любой другой области человеческой деятельности, например:

– при проектировании сложных инженерных сооружений и систем;

– в управлении производственными, техническими и экономическими системами;

– в процессах разработки автоматизированных информационных систем и т.д.

Так, оптимальная система управления может быть реализована в виде набора правил, стратегии или способа управления, согласно которым следует поступать в той или иной ситуации (военной, производственной и т.д.), или в виде комплекса технических средств управления (космическим или морским объектом, инженерным проектом и т.д.).

Поиски оптимальных решений привели к созданию специальных математических методов, и уже в XVIII в. были заложены математические основы оптимизации (вариационное исчисление, численные методы и др.). Однако до второй половины ХХ в. методы оптимизации во многих областях науки и техники применялись редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев – невозможно. Например, большие трудности возникают при решении задач оптимизации процессов в химической технологии из-за большого числа параметров и их сложной взаимосвязи между собой. При наличии ЭВМ задача заметно упрощается.

Постановка задачи оптимизации предполагает существование следующих условий:

1. Наличие объекта оптимизации и цели оптимизации. Формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критерия оптимизации (практически всегда экстремум одного критерия не соответствует экстремуму другого).

---

Вот типичный пример неправильной постановки задачи оптимизации: “Получить максимальную производительность при минимальной себестоимости”. Ошибка заключается в том, что ставится задача поиска оптимума двух величин, противоречащих друг другу по своей сути. Правильная постановка задачи могла быть следующая: “Получить максимальную производительность при заданной себестоимости или получить минимальную себестоимость при заданной производительности”.

В первом случае критерий оптимизации – производительность, а во втором – себестоимость.

2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы – управляющими воздействиями.

3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.

4. Учет ограничений.

Часто оптимизируемая величина связана с экономичностью работы рассматриваемого объекта. Оптимизируемый вариант работы объекта должен оцениваться критерием оптимальности, под которым понимается количественная оценка оптимизируемого качества объекта.

На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.

Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.

Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность). Иногда, в частных задачах оптимизации, когда объект является частью технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить технологическая характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход продукта, степень превращения, температура).

---

В задачах оптимизации важным моментом является использование системного подхода при постановке задачи. Сущность системного подхода заключается в комплексном, едином рассмотрении всех частей системы и их эффективном сочетании. Так, при космических полетах можно, увеличивая вес корабля, добиться максимальной автономии управления, независимо от Земли. Можно, наоборот, обеспечив хорошую связь с кораблем, больше аппаратуры разместить на Земле, максимально уменьшив вес корабля. Оптимальную границу распределения веса наземной и бортовой аппаратуры должны определить методы оптимизации исходя из критерия оптимальности и состояния техники, доступной проектировщикам.

Процесс проектирования любой системы включает в себя, как правило, следующие этапы:

– создание математической модели процесса, которым требуется управлять (объекта управления), и системы управления с обратными связями (контура управления);

– нахождение формального (математического) закона (описания) управления для полученной модели;

– разработка (приобретение) системного программно-технического комплекса управляющей информационно-вычислительной системы и средств связи;

– разработка информационного и программного обеспечения.

На каждом из этих этапов возникает проблема формулировки критериев оптимальности и оптимизации. Так, на этапе разработки информационного и программного обеспечения необходимо решать задачи оптимизации программирования, т.е. задачу порождения компилятором выходной программы, которая наилучшим способом использует ресурсы ЭВМ. При этом задача разбивается на ряд подзадач, например:

– глобальная оптимизация программирования – переупорядочивание установленной последовательности выполнения команд с целью исключения избыточных вычислений;

– регистровая оптимизация программирования – привязка регистров ЭВМ к переменным и промежуточным результатам, чтобы минимизировать число случаев “холостого” резервирования регистров;

– локальная оптимизация программирования – адаптация программы к конкретным особенностям архитектуры ЭВМ.

Хотя системный подход подразумевает общую оптимизацию всех этапов, каждый из них в отдельности может и не быть оптимальным.

---

Для решения задач оптимизации прежде всего необходимо уметь формулировать критерии оптимальности и владеть методами (процедурами) оптимизации.

---

1.2. Классические основы оптимизации

Классические основы оптимизации определяются методами исследования функций в математическом анализе.

Известно, что функция f(x) имеет локальный минимум в точке х₀ ,если существует некоторая положительная величина d, такая, что если Ѕх - х₀Ѕ <d, то f(x) ≥ f(x₀), т.е. если существует окрестность точки x₀, такая, что для всех значении х в этой окрестности f(x) больше f(x₀). Функция f(x) имеет глобальный минимум в точке х*, если для всех х справедливо неравенство f(x) ≥ f(x*).

На рис.1а дано графическое представление функции f(x), которая имеет локальный минимум в точке x₀ и глобальный минимум в точке х^*.



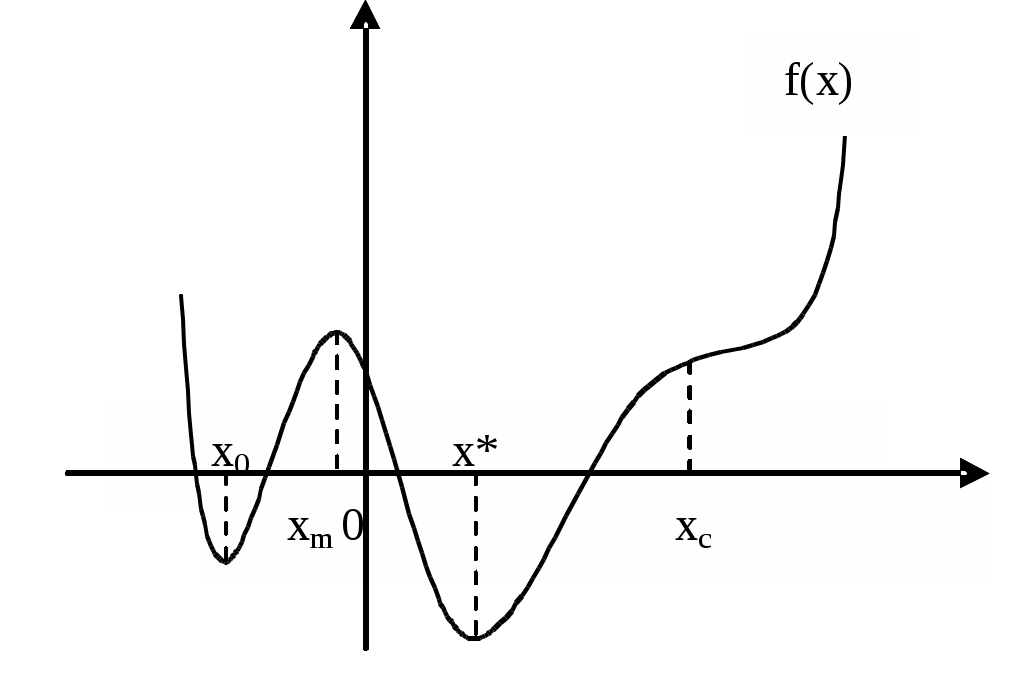
Рис. 1 а. Локальный и глобальный минимумы
Классический подход к задаче нахождения значений x₀ и х^* состоит в поиске уравнений, которым они должны удовлетворять. Представленная на рис. 1а функция и ее производные непрерывны, и видно, что в точках x₀ и х^* производная f’(x) (градиент функции) равна нулю. Следовательно, x₀ и х^* будут решениями уравнения

f’(x) = 0.

Точка x_m, в которой достигается локальный максимум, и точка x_с, в которой имеется точка горизонтального перегиба функции, также удовлетворяют этому уравнению. Следовательно, уравнение f’(x) = 0 является только необходимым условием минимума, но не является достаточным условием минимума.

Заметим, однако, что в точках x₀ и х* производная f’(x) меняет знак с отрицательного на положительный. В точке x_m знак меняется с положительного на отрицательный, в то время как в точке x_c он не меняется. Следовательно, производная в минимуме является возрастающей функцией, а поскольку степень возрастания f’(x) измеряется второй производной, можно ожидать, что f”(x₀)>0, f”(x^*) > 0, тогда как f”(x

---