Добавлен: 09.01.2024
Просмотров: 136
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
C = c1pср + c2wср,
где pср — среднее число свободных приборов; wср — среднее число заявок, ожидающих своей очереди; c1 и с2 — стоимости простоев одного прибора и заявки, соответственно, в единицу времени.
Из-за случайности потока заявок и времени их обслуживания всегда имеется какое-то среднее число простаивающих приборов или ожидающих заявок. Требуется так распределить число приборов по разным системам, чтобы С = min. Такая кибернетическая модель и критерии широко используются при создании оптимальных систем управления в сфере обслуживания, например управления системой гостиниц. В качестве заявок здесь выступают клиенты, в качестве приборов - администраторы. Поток клиентов и время их обслуживания — случайные величины. Плохо, и когда простаивают администраторы, и когда ожидают клиенты. Минимум функционала
C = c1pср + c2wср
означает оптимальный выбор числа администраторов, основанный на определенной статистике потока клиентов. Для решения задачи должны быть известны значения стоимости простоя клиентов и администраторов. Величины pср и wср являются функциями числа приборов на отдельных участках.
В отличие от предыдущих случаев, эта задача имеет дело с дискретным изменением параметров, так как число приборов может изменяться только дискретным образом. Поэтому здесь неприменимо классическое вариационное исчисление, и необходимо применять специальные методы типа дискретного и целочисленного программирования.
Критерий минимума критического времени выполнения работы – это минимизация критического пути по графу при ограниченных ресурсах.
В связи с интенсивным внедрением сетевых методов планирования и управления возникают задачи о критическом пути. Например, выполнение сложного проекта сводится к последовательности выполнения какого-то определенного количества работ. Для отображения этого процесса прибегают к геометрической интерпретации с помощью графа (рис. 6).
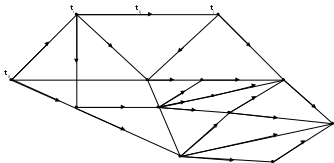
Рис. 6. Сетевой граф комплекса работ
Узел графа обозначает конец одной работы и начало другой. Дуга, или ребро, графа - работа, а длина ребра пропорциональна времени выполнения работы. Пусть длительность выполнения отдельной работы
tij = tj - ti,
где ti и tj — моменты времени, соответствующие началу и концу работы.
Критическим в графе будет такой путь, на котором суммарное время выполнения работ максимально. Этот путь задерживает всю разработку: без его уменьшения невозможно сократить время выполнения всей разработки. Критический путь определяется решением экстремальной задачи, в которой обращается в максимум следующее выражение:
tкр =
Суммирование в этой двойной сумме необходимо производить таким образом, чтобы получить путь из начальной вершины t0 в конечную tк без разрыва и дважды не пройти по одной и той же дуге. Критерий минимума критического времени
I = tкр min
означает минимизацию критического пути при ограниченных ресурсах. При этом наличные ресурсы распределяются на те работы, которые лежат на критическом пути. В данном случае, по существу, решается минимаксная задача, характерная для теории игр:
min max
причем максимум выбирается среди всех путей в графе по времени выполнения работ, а минимум берется по ресурсам для работ, лежащих на критическом пути.
Минимаксный критерий – используется для определения оптимальной стратегии при наличии ситуации, когда интересы двух сторон противоположны.
Минимаксный критерий широко используется для определения оптимальной стратегии при наличии конфликтной ситуации, когда интересы двух сторон противоположны, т.е. выигрыш одной стороны означает проигрыш другой. В этом случае часто приходится выбирать среди худших для себя стратегий противника наименее худшую, т.е. брать максимум по множеству стратегий противника и минимум по собственным стратегиям. В этом и заключается минимаксный критерий, широко используемый в теории игр. В теории матричных игр задается матрица платежей
||aij||,
где i= 1, 2, ..., m; j = 1, 2, ..., n.
Каждый элемент этой матрицы означает платеж противнику в случае
, когда он применяет стратегию j, а наша сторона - стратегию i. Требуется найти среди множества худших для нас стратегий противника наименее плохую, т.е. решить минимаксную задачу
min max aij = ?
i j
Нетрудно убедиться, что если поменять знаки аij на обратные, а это физически означает замену проигрыша нашей стороны на выигрыш, то будет решаться максиминная задача
max min (-аij) = ?
i j
В некоторых задачах, имеющих так называемую седловую точку,
min max aij = max min aij.
i j i j
1.4. Классификация методов оптимизации
Классификация методов оптимизации представляет собой достаточно сложную задачу, так как в основном они исторически развивались независимо один от другого с использованием различных концепций, математических аппаратов и т.д. Однако специалисту по информатике и вычислительной технике необходимо ознакомиться с ними.
Разумеется, что приводимая классификация (как и любая классификация) носит условный характер, но в целом она позволяет сразу охватить все особенности методов.
Возможно несколько подходов к классификации. Следует различать методы определения экстремума функции и функционала (рис. 7). Поскольку функция является частным случаем функционала, методы отыскания экстремума функции проще. Методы динамического программирования и принципа максимума применяются для отыскания экстремума функционала и функции. Прямые методы вариационного исчисления (методы Ритца, Эйлера и др.), как и дискретный вариант уравнения Эйлера, сводят задачу отыскания экстремума функционала к экстремуму функции.
Методы отыскания экстремума функции получили большое развитие в связи с вычислительными трудностями решения системы алгебраических уравнений вида
dF (x1, x2, ..., xn)/dxj = 0, j = 1, 2, ..., n,
особенно при наличии ограничений на координаты xj.
Классическая математика ограничивалась разработкой методов решения и доказательствами принципиальной разрешимости таких систем уравнений, что привело к созданию аналитических методов оптимизации (методы принципиальной разрешимости уравнений оптимизации). При решении конкретных задач важно владеть процедурами, позволяющими доводить решение до числовых данных. Это заставило искать и разрабатывать численные методы оптимизации (методы решения конкретных инженерных задач с доведением решения до числовых данных). Практика проектирования конкретных систем управления требует применения обоих методов.
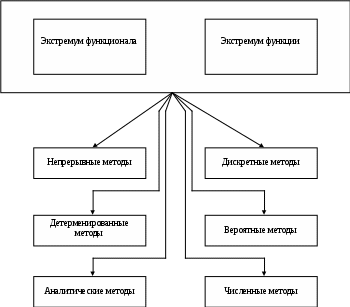
Рис. 7. Схема методов оптимизации
За аналитическими методами остается преимущество, заключающееся в возможности определения качественной картины поведения оптимальной системы при изменении ее параметров и структуры. Численные же методы обеспечивают получение конкретных числовых значений параметров. Рациональное объединение этих методов производится при разработке человеко-машинных методов оптимизации, использующих диалог человека и ЭВМ, базы данных и возможности современных телекоммуникационных систем. При этом обычно повторяют вычисления, изменяя условия, используя, где необходимо, аналитические методы, представленные в виде стандартных библиотечных программ, и, самое главное, оперативно включая в процедуру отыскания оптимального управления интеллектуальные способности человека.
При таком способе оптимизации исходный критерий оптимальности может быть математически нестрого формализован в виде функции или функционала. Так, он может состоять из нескольких положений, сформулированных достаточно четко на словесном, содержательном уровне, что при наличии диалога человек-машина вполне допустимо.
В задачах с ограничениями большое развитие получили методы линейного и нелинейного программирования, прямые методы отыскания экстремума функции, а также дискретные принципы максимума и динамическое программирование (рис. 8).
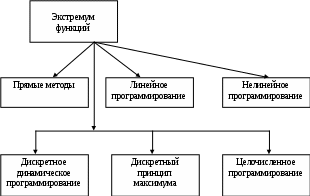
Рис. 8. Методы отыскания экстремумов функций
Методы отыскания экстремума функционала ведут свое начало от классических методов Эйлера-Лагранжа-Гамильтона и заканчиваются динамическим программированием и принципом максимума (рис. 9). В них также содержатся прямые методы отыскания экстремума функционала и различные частные методы.
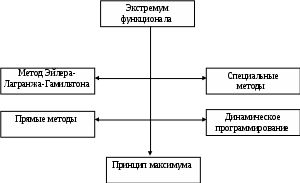
Рис. 9. Методы отыскания экстремумов функционалов
Почти во всех методах:
– Эйлера — Лагранжа — Гамильтона;
– принципе максимума;
– динамическом программировании;
– прямых методах отыскания экстремума функции
можно выделить дискретные и непрерывные модификации, детерминированные и случайные варианты.
Дискретная задача оптимизации возникает всякий раз, когда требуется найти оптимальное значение переменных, которые заданы, так же как и функция от них, в виде набора дискретных значений.
В связи с разработкой автоматизированных информационных систем управления (АИСУ) большое значение приобрели методы целочисленного программирования. Одна из основных задач АИСУ – оперативно-календарное планирование, относится к задачам целочисленного программирования. Единого общего метода решения задач целочисленного программирования нет. Разработано много способов решения пригодных для частного класса задач, среди которых большое место занимают нестрогие эвристические методы. Особого внимания среди них заслуживают лингвистические методы оптимизации (методы, имитирующие применяемые человеком методы оптимизации и планирования с добавлением эффективных аналитических и числовых процедур). Они ближе всего подходят к человеческому способу мышления и удобны для реализации на ЭВМ с помощью проблемно-ориентированных языков. Человеко-машинные методы решения целочисленных задач оптимизации являются по существу своему лингвистическими в широком смысле.