Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 381

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Свободные гармонические незатухающие колебания. Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: (3).Его решением является гармоническая функция: (4), в чем легко убедиться, подставив (4) в (3).В (4) xm , ω0 и φ0 – постоянные величины. xm– амплитуда – величина, указывающая максимальное значе­ние координаты х при отклонении от положения равновесия, ω0 – собственная частота, аргумент косинуса носит название фазы колебания; φ0 — начальная фаза коле­бания (в момент t= 0). Частота колебаний зависит только от свойств колеблю­щейся системы, но не от амплитуды, а амплиту­да и начальная фаза колебаний определяются начальными условиями ее движения, выводя­щими систему из состояния покоя.Скорость колеблющейся частицы равна: (5). Ускорение частицы при таком движении: (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0=0.Складывая кинети­ческую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы: (7).Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потен­циальная энергии изменяются со временем, как sin2(ω0·t+φ0) и cos2(ω0·t+φ0) , так что когда одна из них увеличивает­ся, другая – уменьшается, т.е. процесс колеба­ний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Сред­ние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения час­тицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x , действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса).Примечание: В механике обычно рассматривают колебания : – математического маятника с периодом , где ℓ–длина маятника;– физического маятника с периодом , где J–момент инерции маятника, a–расстояние от точки подвеса маятника до его центра масс;– пружинного маятника с периодом , где k–жесткость пружины.2. Свободные затухающие колебанияПри наличии силы трения (r ≠0) и отсутствии внешней периодической силы (F0 =0) уравнение движения имеет вид: (8),г де β называется коэффициентом затухания колебаний. В случае слабого затухания (β – мало) решением такого дифференциального уравнения является функция : (9). В этом можно убедиться прямой подстановкой (9) в уравнение (8). – частота колебаний системы с затуханием. A=A0·e-βt – амплитуда затухающих колебаний.Таким образом, амплитуда колебаний убыва­ет по экспоненциальному закону. Вместе с амплитудой убывает также и энергия колебаний W, т.к. WA2.Степень убывания амплитуды определяется коэффициен­том затухания β. Время τ=1/β, за которое амплитуда колебаний уменьшается в е=2.7183 раз, называют по­стоянной времени затухания колебаний.Скорость уменьшения амплитуды за период характеризует величина θ, называемая лога­рифмическим декрементом затухания. По определению: (10).Скорость убывания энергии в системе с зату­ханием характеризует добротность Q: (11),где W – энергия, запасенная в системе, (–ΔW)– энергия, теряемая системой за период. Добротность показывает, во сколько раз энер­гия, запасенная в системе, больше энергии, те­ряемой за период. Добротность в (11) выражена через параметры системы и логарифмический декремент затухания θ, с учетом того, что W

1.10. ОСНОВЫ ТЕРМОДИНАМИКИТермодинамика– учение о превращениях одного вида энер­гии в другой, о передаче энергии от тела к телу. Термодинамика изучает свойства макроскопических тел без рассмотрения их молекулярной структуры. Термодинамическая система (ТС) –макроскопические тела, которые могут обмениваться энергией как друг с другом, так и с внешней средой.Равновесное состояние ТС - состояние, при котором термодинамические параметры (давление, температура и объем) остаются постоянными сколь угодно долго при неизменных внешних условиях. Термодинамический процесс – изменение состояния ТС, характеризующееся изменением ее параметров. Состояние ТС характеризуют также внутренней энергией, которая равна сумме кинетических энергий беспорядочного движения всех молекул и потенциальных энергий взаимодействия молекул друг с другом. Система тел называется изолированной, или замкнутой, если нет обмена энергией с окружающей средой. Первое начало термодинамикиТела и системы могут обмениваться энергией друг с другом. Существует два вида обмена энергией. Это может быть работа, произведенная одним телом (системой) над другим телом (сис­темой). Примером мо­жет служить перемещение тела или его частей под действием упругих, электрических или других сил.Другой способ обмена энергией – путем передачи энергии неупорядоченного, хаотического движения молекул. Тогда гово­рят о передаче тепла. Например, передача энергии от нагретого тела к холодному происходит за счет передачи кинетической энергии хаотически движущихся молекул одного тела хаотичес­кому движению молекул другого тела. В обоих этих случаях изменяется внутренняя энергия U.Сказанное выше можно записать как: ΔU = Q+А’, где Q – энергия,поступающая в систему при теплообмене, а А’– работа, совершаемая внешнимителами над системой. Исторически принято это соотношение записывать как: Q = ΔU + А (18), где А = – А’ –работа, совершаемая самой системой.(18), представляющее собой закон сохранения энер­гии, получило название первого начала термодинамики: «Подведенное к телу количе­ство теплоты идет на увеличение внутренней энергии тела и на работу, которую тело производит». Очень важно отметить различие между величинами U с одной стороны, и А и Q – с другой. Внутренняя энергия U– это функция состояния системы. Если в состоянии 1 внутренняя энергия равна U1 , то что бы ни происходило с системой, какую бы работу она ни соверша­ла, какие бы количества теплоты к ней ни подводились, если систе­ма вернулась в то же состояние 1 (т. е. процесс оказался круговым, совершен цикл), ее внутренняя энергия будет снова U1 (ΔU=0).В то же время Q и А – это только передаваемые телу или получаемые от тела порции энергии. Они связаны с передачей энергии, а не с каким-то запасом их в теле. Бессмысленно гово­рить о запасе работы в теле. И так же бессмысленно говорить о запасе теплоты в теле. Работа и теплота не являются функция­ми состояния тела. Переходя к бесконечно малым порциям энергии, запишем первое начало в дифференциальной форме: δQ = dU + δA. (19).Здесь специально даны разные обозначения бесконечно малых («d...» и «δ…»), чтобы отразить то обстоятельство, что U – функ­ция состояния, a Qи А – нет. Работа расширения идеального газа при различных процессах На рисунке а приведена зависимость давления газа от его объема. Точка 1 означает состояниегаза, так как указывает его дав­ление и объем в данный момент. Температуру при этом можно найти из (4). Линии означают процессы, так как показывают, через ка­кие состояния система проходит. Процесс может быть без изменения давления (прямая I на рисунке а). Такой процесс называется изобарическим. Изохорическийпроцесс (прямая II) – это процесс без изменения объе­ма. Процесс без изменения температуры (изотермический)будет примерно та­ким, как показано кривой III. Это гипербола, так как при Т = const давление обратно пропорционально объему: p

Взаимодействие зарядов. Известно, что одноименные заряды отталкиваются, разноименные - притягиваются. Закон взаимодействия точечных зарядов впервые сформулировал Кулон в 1785 г. (закон Кулона) : , где q, Q - взаимодействующие заряды,  -единичный вектор в направлении радиус-вектора , r - расстояние между зарядами; сила направлена вдоль прямой, соединяющей заряды. ε0 = 8.85·10-12 Ф/м – электрическая постоянная.Электрическое поле .      Запишем закон Кулона в виде:       .   Теперь его можно прочитать так: сила взаимодействия двух зарядов равна произведению первого заряда q на нечто, что зависит только от второго заряда Q и от расстояния до него.  Это нечто и называется электрическим полем заряда Qили - более строго - напряжённостью электрического поля, создаваемого зарядом Q. Напряженность– векторная характеристика электрического поля, численно равная силе, с которой поле действует на единичный электрический заряд, помещенный в рассматриваемую точку поля: .(Поле не просто удобный математический способ описания взаимодействия, а еще одна форма существования материи (наряду с веществом); о его наличии мы судим по силовому воздействию на пробные тела). Если заряд q взаимодействует с несколькими зарядами, можно сказать, что он взаимодействует с электрическим полем, созданным этими зарядами, при этом электрическое поле вычисляется как векторная сумма полей от каждого заряда (принцип суперпозиции): .Потенциал              Электростатическое поле - консервативное силовое поле, то есть работа сил поля A над зарядом q не зависит от траектории движения заряда, а определяется его начальным и конечным положениями. Работу сил такого поля при перемещении заряда q можно представить как разность некоторой функции координат U(r) в начальном и конечном положениях заряда. (Эту функцию координат U(r) называют потенциальной энергией взаимодействия зарядов). Найдём работу А, совершаемую полем, созданным точечным зарядом Q, при перемещениизаряда q из точки 1 в точку 2: .Потенциальной энергией взаимодействия зарядов q и Q будет : , где величина – называется потенциалом точечного заряда  Q в точке  пространства на расстоянии r от него.Потенциал φ - это скалярная характеристика электростатического поля, численно равная потенциальной энергии единичного заряда, помещенного в данную точку поля.В системе единиц СИ напряженность измеряется в Н/Кл=В/м, а потенциал в Дж/Кл=В (Вольт).Связь напряженности электрического поля и потенциала. Теорема о циркуляции вектора .        И напряжённость и потенциал описывают один объект – электростатическое поле.  Найдем связь между ними, исходя из выражения для работы в дифференциальной форме: .Если поделить это выражение на величину пробного заряда q, то получим или или для одномерного случая. В общем виде это выражение записывается как: (произносится так: «напряженность поля равна со знаком минус градиенту потенциала φ») , где . Можно также вычислить разность потенциалов двух точек поля: . Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность: . Если единичный заряд возвращается в начальную точку, то работа электростатических сил по замкнутому контуру равна нулю: . Это соотношение носит название теоремы о циркуляции, а сам интеграл называется циркуляцией вектора по замкнутому контуру ℓ.Линии поля Для наглядности принято изображать векторное электрическое поле в пространстве (или на плоскости) с помощью линий электрического поля, которые строятся по следующим правилам: - вектор электрического поля в каждой точкепространства направлен по касательной к линии поля в этой точке; - направление вектора поля совпадает с направлением линии поля; - густота линий поля отражает величину вектора поля в данной области пространства; - линии поля начинаются на положительных зарядах и кончаются наотрицательных; либо приходят из бесконечности и уходят в бесконечность; - поскольку в каждой точке пространства поле определено однозначно, линии поляне могут пересекаться. Эквипотенциальные поверхности Г еометрическое место точек в пространстве, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью (на плоскости - эквипотенциальной линией).  Из связи между вектором электрического поля и потенциалом следует, что эквипотенциальные поверхности всегда перпендикулярны линиям электрического поля. Действительно, если две точки на расстоянии dr имеют одинаковые потенциалы (т.е., dφ=0), то из соотношения dφ = - E·dr·cosα = 0, следует, что вектор и вектор , соединяющий две точки на эквипотенциали, взаимно перпендикулярны (α=900). Если между соседними поверхностями одинаковая разность потенциалов, то густота эквипотенциалей, как и густота линий поля, будет отражать величину электрического поля в пространстве.Теорема Гаусса Потоком напряжённости электрического поля (или просто потоком электрического поля) dФ в вакууме через площадку dS называется величина: . Вектор площади направлен по нормали к её поверхности, а его модуль равен площади площадки dS. (У площадки две стороны, поэтому всегда надо оговаривать, какую нормаль принимать за положительную) . Рассчитаем поток вектора через сферическую поверхность радиусаr для поля, создаваемого точечным зарядом q, находящимся внутри этой поверхности : . Этот результат оказывается справедливым для замкнутой поверхности произвольной формы и для любого количества зарядов внутри такой поверхности и получил название теоремы Гаусса для электростатического поля в вакууме. Теорема Гаусса: поток вектора напряжённости электростатического поля сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов , охватываемых поверхностью S, деленной на электрическую постоянную ε0: ..Н апряженность и потенциал поля заряженной плоскости Для вычисления поля, создаваемого бесконечной заряженной плоскостью, воспользуемся теоремой Гаусса, и в качестве гауссовой поверхности выберем куб со стороной 2r. Очевидно, что линии поля направлены перпендикулярно влево и вправо от плоскости, поэтому поток поля через поверхность куба будет состоять только из потока через две стороны куба, перпендикулярных линиям поля и параллельных плоскости. Теорема Гаусса запишется в виде: .Таким образом, бесконечная заряженная плоскость создаёт в пространстве однородное поле: . За нуль потенциала примем потенциал плоскости; тогда потенциал φ=φ2 поля на расстоянии х от плоскости будет: .Графики напряженности и потенциала поля заряженной плоскости: Расчеты напряженности и потенциала полей, создаваемых заряженными шаром и цилиндром проводятся аналогично. Конденсатор.         Две бесконечные пластины, заряженные одинаковыми по величине, но разноимёнными зарядами, создают поле, сконденсированное между пластинами; за пластинами поле отсутствует (между пластинами поля от каждой пластины арифметически складываются: E=σ/ε0 , за пластинами – вычитаются E=0). П одобные устройства называются конденсаторами электрического поля или просто конденсаторами. Обычно рассматривают плоские, сферические или цилиндрические конденсаторы. Проводники Проводниками называют вещества, содержащие свободные электрические заряды, то есть такие, которые могут свободно перемещаться по объёму проводника под действием электрического поля. Все металлы являются проводниками.При помещении незаряженного изолированного проводника во внешнее электрическое поле свободные электрические заряды под действием внешнего поля перемещаются так, что края проводника оказываются заряженными; индуцированные на краях проводника заряды создают собственное поле; разделение зарядов продолжается до тех пор, пока внешнее поле и поле индуцированных зарядов не сравняются по величине; при этом суммарное поле в проводнике исчезнет, движение зарядов прекратится.Е сли зарядить изолированный проводник, то избыточные электрические заряды отталкиваются и распределятся только на поверхности проводника. Так как внутри проводника нет нескомпенсированных электрических зарядов, то, согласно теореме Гаусса, электрическое поле и внутри заряженного проводника равно нулю. Заряды должны распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовала бы разность потенциалов, что приводило бы к перемещению зарядов, то есть отсутствию равновесия. Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника.  Его легко рассчитать по теореме Гаусса: . Это поле не приводит к движению зарядов, ибо заряды не могут покинуть проводник (на поверхности металла существует потенциальный барьер, "запирающий" электроны внутри металла, так называемая "работа выхода электрона из металла").2.2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ.Э лектрический диполь. Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга.  Дипольный момент (или электрический момент диполя) - вектор; его направление - от отрицательного заряда к положительному. Электрическое поле диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно: .θ - угол между дипольным моментом и направлением на точку пространства, в которой вычисляется поле. Формула применима для расстояний r >> ℓ.  Поле диполя с расстояниемr спадает быстрее ( ), чем поле точечного заряда (

Электромагнитная индукция. Правило Ленца Опыт показывает, что если в катуш­ку, соединенную с гальванометром, вдви­гать постоянный магнит (рис. а), то гальванометр покажет ток тогда, когда магнит движется. Если магнит, наоборот, удалять из ка­тушки, то в ней идет ток обратного направления.Это явление, открытое Фарадеем, называет­ся электромагнитной индукцией, возникающий ток называется индукционным током, а распре­деленная по катушке э.д.с., под действием кото­рой течет ток, называется э.д.с. индукции. Причем э.д.с. индукции возникает в контуре всегда, а ток – только, если контур замкнут и яв­ляется проводником. Существенно именно не движение магнита, а изменение магнитного потокаФ через катушку. Например, в опыте, изображенном на верхнем рис., во внутреннем контуре возникает индукционный ток, если во внешнем с помощью реостата менять силу тока, получае­мого от внешнего источника. Причем, если во внешнем кон­туре ток увеличивать, так что поток Ф, создаваемый этим током, растет, то вовнутреннем контуре возникает индукционный ток противоположного направления. Он своим магнитным потоком Фi будет препятствовать нарастанию потока Ф. Если же силу тока в одном из конту­ров и, следовательно, поток Ф, уменьшать, например, разомкнув цепь внутреннего контура на нижнем рис., то в другом контуре возникнет индукционный ток и маг­нитный поток Фi того же направления, чтобы препятствовать уменьшению потока Ф.Ленц сформулировал это следующим образом (правило Лен­ца): индукционный ток возникает такого направления, что он своим магнитным действием препятствует той причи­не, в результате которой он возник.Формула Фарадея для э.д.с. индукцииИ спользуя закон сохранения энергии, получим формулу для э.д.с. индукции. Рассмотрим схему на рис. Перемычку будем сами двигать влево. При этом поток Ф, пронизывающий кон­тур, будет уменьшаться на dΦ. Возникает индукционный ток Iтакого направления, что действующая на него сила Ампера FA согласно правилу Ленца препятствует движению.Будет совершена работа по передвижению провода с током в магнитном поле: dA = –I·dΦ. Знак «–» поставлен потому, что работу совершают сторонние силы, а не силы поля. Эта работа приводит к возникновению э.д.с. индукции εинд, индукционного тока и к выделению тепловой энергии в цепи: dA = I· εинд·dt. Приравнивая выражения для работ, получим формулу Фарадея для э.д.с. индукции: εинд=–dΦ/dt . Эта э.д.с. является результатом действия сторонних сил и может быть записана в виде: .В это выражение не входят величи­ны, отражающие какие-либо свойства материа­ла, из которого сделан контур. Следовательно, э.д.с. электромагнитной индукции от этих свойств не зависит. Это позволяет считать, что измене­ние магнитного поля вызывает появление элект­рического поля. Ток, протекающий в контуре, является следствием электрического поля.Если контур состоит из N витков, то индуцируе­мая в контуре э.д.с. будет равна сумме э.д.с. , инду­цируемых в каждом из витков в отдельности: .Величина называется потокосцеплением, или полным магнитным потоком. Если по­ток, пронизывающий каждый из витков, одина­ков, то Ψ=N·Φ.Приведем выражения для э.д.с. индукции при различных способах ее возбуждения:− э.д.с. индукции, возникающая в проводнике длиной ℓ, движу­щемся под углом α к силовым линиям со скоростью υ: ; − э.д.с. индукции, возникающая в контуре , вращающемся в магнитном поле: ;− э.д.с. индукции, возникающая в контуре при изменении его площади: ;− э.д.с. индукции, возникающая в контуре, помещенном в изменяющееся магнитное поле: . Самоиндукция Э.д.с. индукции может возникать и в самом контуре с меняющимся токомI. Другого контура при этом может и не быть. При усилении тока (и следовательно, увеличении потока Ф) в контуре воз­никает э.д.с. индукции и индукционный ток Iинд такого направления, чтобы препятствовать усилению тока I. Это явление носит на­звание самоиндукции. Так как магнитный поток Ф, пронизывающий контур, пропорционален силе тока: Ф = L·I , то э.д.с. самоиндукции пропорциональна скорости изменения тока: , где L – коэффициент самоиндукции или индуктивностька­тушки.Найдем индуктивность длинного со­леноида. Поток Ф через один виток равен B·S. Через все N витков соленоида Ψ = N·B·S. Индукция в соленоиде равна B=μ0·(N/ℓ)·I. Так что .Сравнивая два выражения, найдем: , где V=S·ℓ–объем внутри соленоида, ℓ– длина соленоида, n–число витков на единице длины соленоида (густота намотки). Т.о., индуктивность соленоида очень сильно зависит от густоты намотки n. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ Магнетики. Напряженность магнитного поля.Все вещества являются магнетиками, т.е. при помещении их во внешнее магнит­ное поле изменяют свое состояние – намаг­ничиваются. Находясь во внешнем магнитном поле, намагниченные вещества сами становят­ся источниками поля . Собственное магнитное поле , накладываясь на магнитное поле , в сумме дает .Вещества, в которых поля и направлены одинаково, называют парамагнетиками. Ве­щества, в которых поля и направлены в противоположные стороны, называют диамагнетиками.Степень намагничивания вещества характе­ризуется вектором намагниченности . Это вектор, среднее значение которого равно отно­шению суммарного магнитного момента всех частиц, расположенных в объеме магнетика, к этому объему: , где ΔV– физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, – магнитный момент отдельной мо­лекулы. Суммирование производится по всем молекулам, заключенным в объеме ΔV. Единицей намагниченности является ампер на метр(А/м). Линии вектора и при наличии вещества остаются всюду замкнутыми. Для описания поля , создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины ℓ, внесенного в однородное внешнее магнитное поле с индукцией .В озникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору . Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис.). Некомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.Ток, текущий по боковой поверхности цилиндра I’, подобен току в соленоиде и создает внутри него поле, магнитнуюиндукцию В’ которого можно вычислить, учитывая формулу для соленоида из одного витка: B’=μ0·I’/ℓ,где I’–сила молекулярных токов (т.н. ток намагничи-вания), ℓ – длина рассматриваемого цилиндра. Магнитный момент этого тока P = I’·S= I’·S·ℓ/ℓ = I’·V /ℓ, где S и V — площадь сеченияи объем магнетика, соответственно. Если Р – суммарный магнитный момент магнетика объемом V, то намагниченность магнетика: J=P/V=I’/ℓ. Т.о., получим связь между B’ и J: . Теорему о циркуляции вектора для вещества можно представить в виде: . Если в этом выражении сделать замену: I’= J·ℓ , то получим или, вводя вспомогательный вектор , получивший название напряженности магнитного поля,: . Это выражение очень удобно, так как в правой части не содержит микро- (молекулярные) токиI’, которые очень трудно оценить, и представляет собой теорему о циркуляции вектора : циркуляция вектора напря­женности магнитного поля по произвольному контуру равна алгебраической сумме макроско­пических токов, охватываемых этим контуром.Вектор намагниченности принято связывать не с магнитной индукцией , а с напряженностью поля : , где безразмерная величина χ называется магнитной восприимчи­востью. Для диамагнетиков χ − отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков χ − положительна (поле молекулярных токов совпадает с внешним).В диа- и парамагнетиках при не очень сильных полях χне зависит от Н и: ,где безразмерная величина μ=1+χ называется магнитной проницаемостью вещества. μ и χ характеризуют магнитные свойства магнетиков.Так как абсолютное значение магнитной восприимчивости χ для диа- и парамагнетиков очень мало (порядка 10–4−10–6), то μ для них незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков μ < 1, для парамагнетиков μ > 1, причем как у тех, так и у других μотличается от единицы весьма мало, т.е. магнитные свойства этих магнетиков выражены очень слабо.Природа магнетизма. Ферромагнетики. Причина усиления в парамагнетиках состоит в том, что ато­мы или молекулы вещества представляют собой магнитные дипо­ли (обладают магнитными моментами). Эти диполи ориентируются во внешнем поле вдоль силовых линий и усиливают его. Если в соленоид вставлен сердечник из пара­магнетика, то дипольные моменты ато­мов (на рис. – стрелки) ориентируются вдоль по полю. В парамагнетике этот эффект очень слаб, и μ близко к единице, так как из-за теплового движения происходит только незначительная преимущественная ориентация диполей вдоль поля (рис.а). В молекулах диамагнетиков магнитный момент отсутствует, но он появляется при помещении диамагнетика во внешнее магнитное поле. Результирующий магнитный момент в диамагнетике мал, всегда направлен против внешнего поля и от температуры не зависит.С уществуют вещества, в которых μ

2.8. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ. Если электрические и магнитные поля изме­няются во времени, то по отдельности их рас­сматривать уже нельзя: взаимное превраще­ние электрических и магнитных полей приводит к появлению электромагнитной волны.Для среды – однородного и изотропного диэлектрика, не обладающего сегнетоэлектрическими или ферромагнитными свойствами, из уравнений Максвелла можно получить, что векторы напряженностей переменного электромагнитного поля удовлетворяют уравнениям: 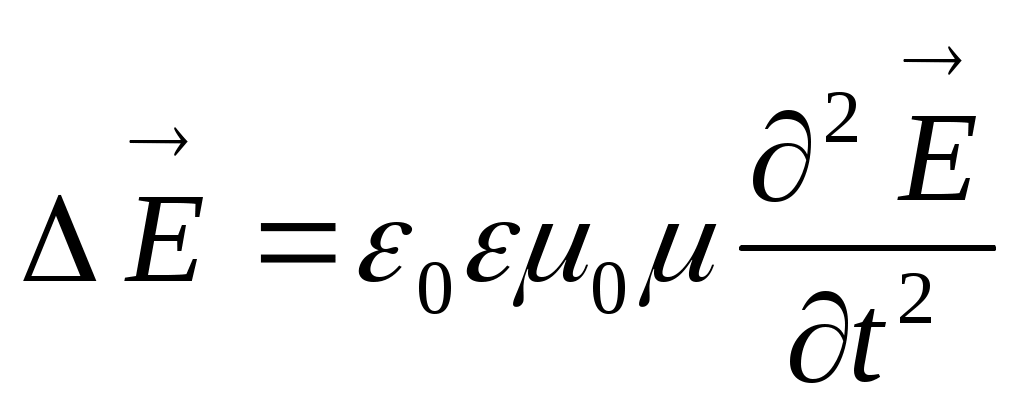и , 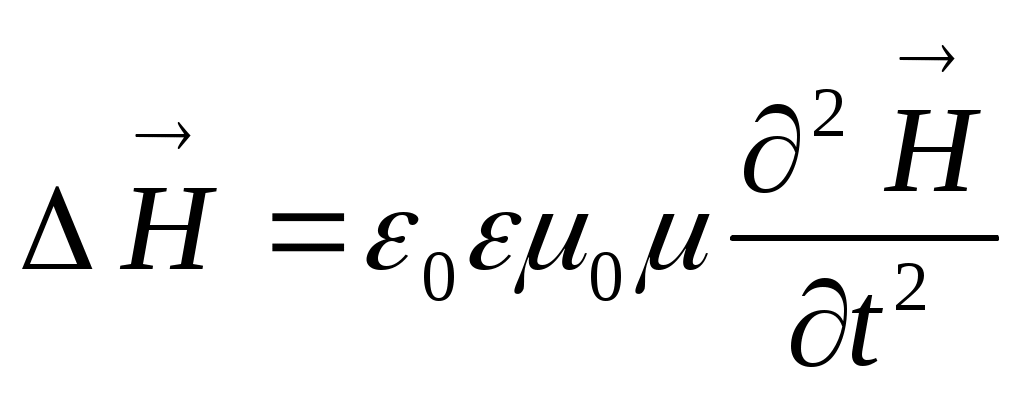где 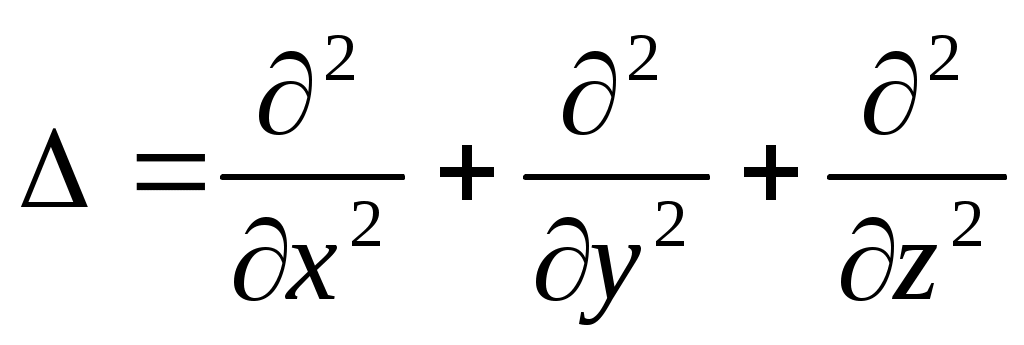- оператор Лапласа. Но это уравнения, описывающие волновой процесс, в которых скорость распространения волны определяется коэффициентом, стоящим перед второй производной по времени: 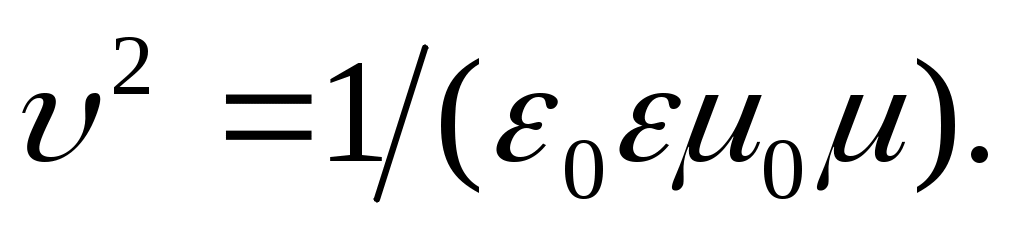Решением этих уравнений является т.н. плоская монохроматическая гармоническая волна: 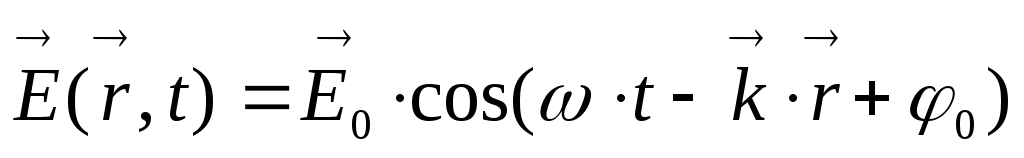, , 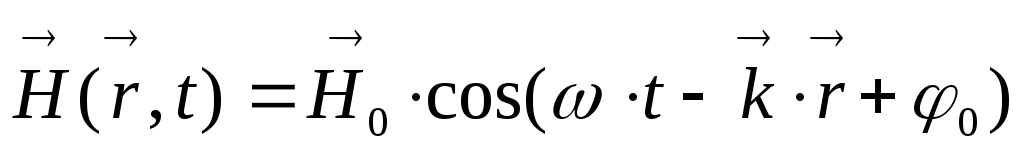где 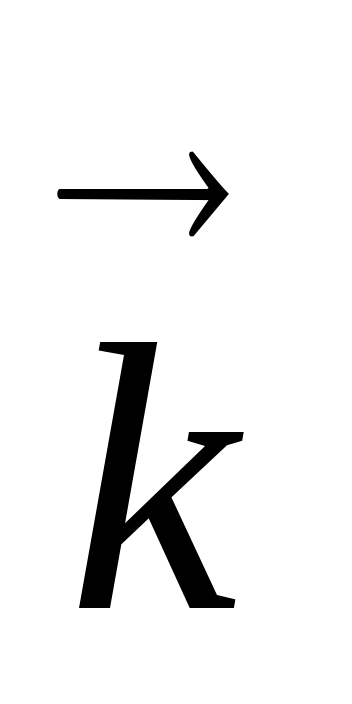- волновой вектор, указывающий направление распространения волны. Т.о., переменное электромагнитное поле действительно распространяется в пространстве в виде волн. Если волна распространяется в вакууме ( 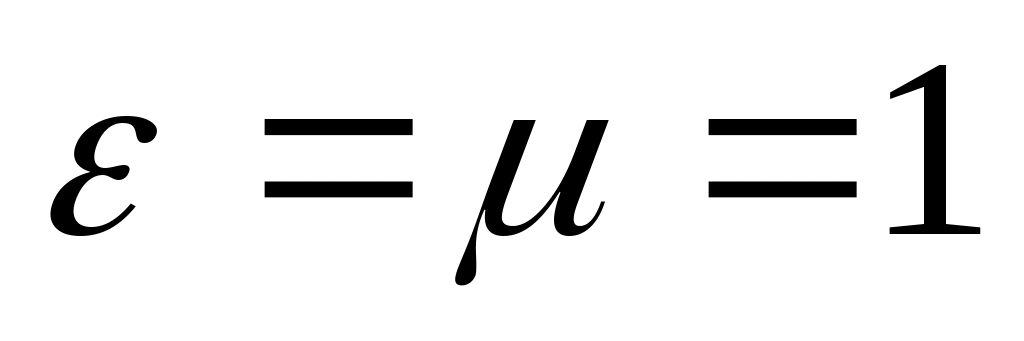), то 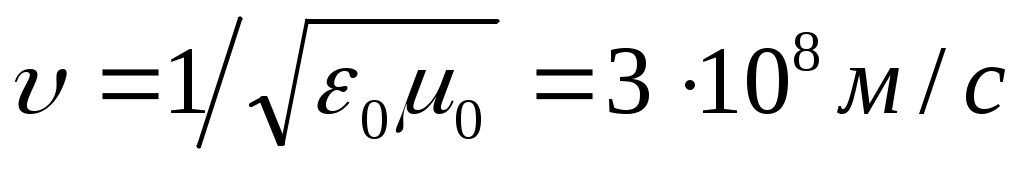. Этот результат в точности совпадает с изме­ренным значением скорости света с, что послу­жило основой для создания электромагнитной теории света. Свойства электромагнитных волн– Электромагнитные волны – поперечные волны; векторы и лежат в плоскости, перпендикулярной к скорости волны 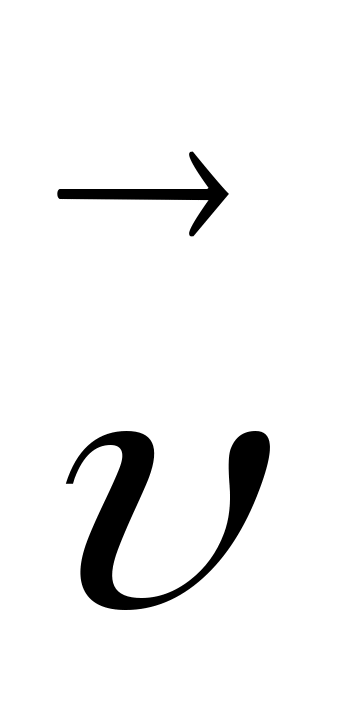в данной точке поля.– Векторы и взаимно перпендикулярны и образуют с направлением распространения волны, т.е. скоростью 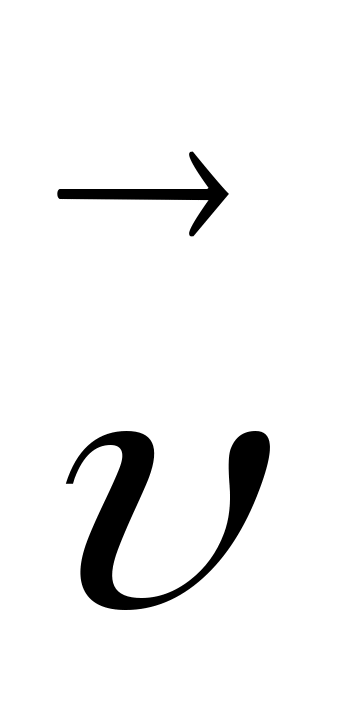, правовинтовую систему (рис.).– Взаимно перпендикулярные векторы и колеблются в одной фазе, причем мгновенные значения EиH связаны соотношением: 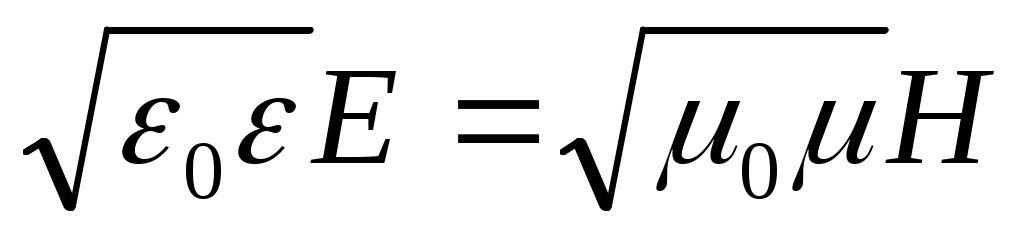, т.е. они д 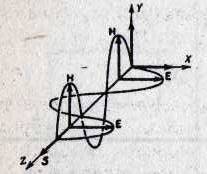остигают максимума и обра­щаются в нуль в одних и тех же точках в одни и те же моменты времени. – В вакууме скорость электромагнитной волны равна с и не зависит от частоты.– Объемная плотность энергии электромаг­нитного поля складывается из объемных плотностей энергии электрического и магнитного полей: 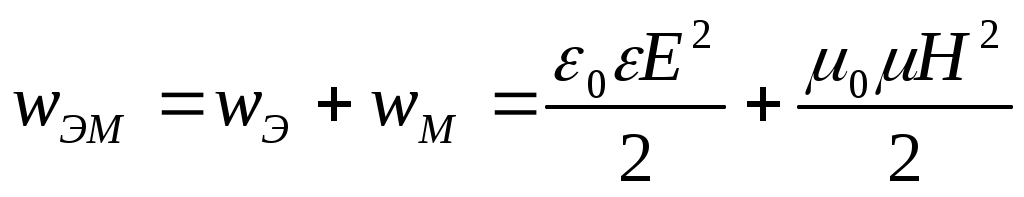. С учетом соотношения, связывающего E и H, получим: 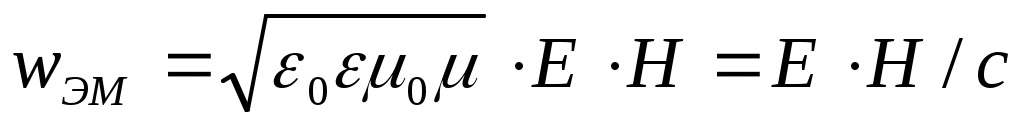.– Направление распространения электромаг­нитной волны и энергию, переносимую волной в единицу времени через перпен­дикулярно ориентированную площадку единичной площади, опреде­ляет вектор Умова—Пойнтинга, аналогичный вектору Умова, введенному для механической волны,: 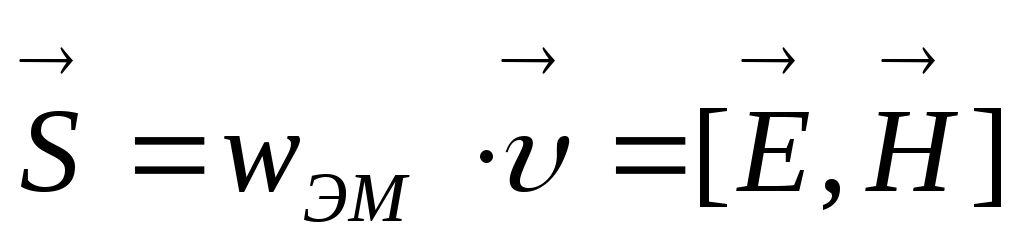. Среднее значение модуля этого вектора представляет интенсивность волны.– Поскольку различные электромагнитные вол­ны имеют общую природу, их можно представить в виде единой шкалы.Вся шкала условно подразделена на 6 диа­пазонов в порядке уменьшения длины волны (возрастания частоты) : радиоволны (длинные, средние и короткие) (от нескольких км до 0,1 мм); инфракрасное излучение (от 0, 1 мм до 0,74 мкм); видимое излучение (от 0,74 до 0,38 мкм); ультрафиолетовое излучение ( от 0,38 мкм до 1нм (10 - 9м )); рентгеновское излучение ( от 1 нм=10 Å до 0,1 Å (1Å=10 -10м )); гамма-излучение ( короче, чем 0,1Å). Радиоволны обусловлены переменными то­ками в проводниках и электронными потоками. В инфракрасной, видимой и ультрафиолетовой областях излучают атомы, молекулы и быстрые заряженные частицы. Рентгеновское излучение возникает при внутриатомных процессах, γ-излучение имеет ядерное происхождение. Частич­но диапазоны перекрываются, т.к. волны одной и той же длины могут излучаться в разных про­цессах. ФИЗИКА. Часть 3. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ СВЕТА . Интерференция света 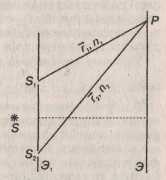Пусть в произвольную точку наблюдения Р на экране Э приходят две волны (рис.): 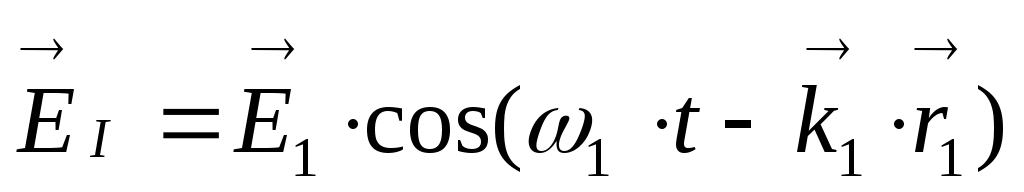и , где ЕI и ЕII – напря­женности электри­ческих полей световых волн, идущих от источников S1 и S2 , ω1 и ω2 – частоты волн, -соответствующие волновые векторы. Сложение таких колебаний (можно применить формулу косинусов) дает: .Если учесть, что интенсивность волны пропорциональна квадрату амплитуды (I

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля. Дифракция – явление отклонения света от прямолинейного распространения в неоднородной среде, при котором свет, огибая препятствия, заходит в область геометрической тени, – возни­кает, когда свет падает на препятствия, размеры которых сравнимы с длиной световой волны.По принципу Гюйгенса, каждую точку фрон­та волны можно рассматривать как самостоя­тельный источник вторичных сферических волн. По Френелю, волновое возмущение в любой точке пространства – результат интерферен­ции этих вторичных когерентных волн. Различают т.н. дифракцию Френеля или сферических волн и дифракцию Фраунгофера или плоских волн.Метод зон Френеля. Волновую поверхность разбивают на зоны так, чтобы расстояния от краев соседних зон до точки наблюдения Pотличались на λ/2 (рис.). В этом случае фазы приходящих от соседних зон колеба­ний отличаются на π , сами колебания противоположны по фазе, поэтому при наложении волн они взаимно ослабляют друг друга. Тогда амплиту­да Eрезультирующих колебаний может быть представлена в виде знакопеременного ряда: Дифракция Френеля на круглом отверстии. Пусть в отверстии помещается m зон. Так как амплитуды сферических волн убывают с увеличением расстояния до т.Р, то приближенно выполняется равенство: Ek=(Ek-1+Ek+1)/2 , т.е. амплитуда волны от k-зоны равна среднему арифметическому амплитуд волн от примыкающих к ней зон. Тогда все выражения в круглых скобках обращаются в нуль и для результирующей амплитуды колебаний в т.Р получим: , где: знак «+» соответствует нечетному числу m зон , открываемых отверстием (например, для m = 5 и наблюдается максимум – светлое пятно); знак «–» соответствует четному числу m зон , открываемых отверстием (например, для m = 4 и наблюдается минимум – темное пятно). Если отверстие будет большим (или экрана вообще не будет), то поместятся много зон и в результате . Это означает, что в т.Р попадает свет только от первой зоны, и таким образом объясняется прямолинейное распространение света. Е сли на место Рпоместить экран, то вокруг точки Р будут минимумы и макси­мумы освещенности, имеющие форму колец.. В центре, т. е. в точке Р, может быть как свет, так и темнота, в зависимости от числа зон Френеля, уместившихся в отверстии. Эти теоретические рас­суждения прекрасно подтвердились на опыте.Но самый поразительный результат был получен при рассмот­рении дифракции на круглом непрозрачном экране(рис.). В этом случае несколько центральных зон (например, m) закрыва­ются, а все остальные зоны открыты. Это значит, что в центре тени от малого предмета всегда должно быть свет­лое пятнышко (рис.) . Оно получило название пятна Пу­ассона. На опыте это подтвердилось, что стало блестящим доказательством волновой природы света.Дифракция Фраунгофера на щелиП лоская электромагнитная волна падает нор­мально на преграду со щелью ширины b. Если бы не было дифракции, световые лучи, пройдя через щель, сфокусировались бы в точ­ке F, лежащей на главной оптической оси линзы (рис.). Однако, наблюдаемое на экране распределение интенсивности света имеет в центре резкий максимум освещенности, относительно которого симметрично располагаются чередуясь светлые и темные полосы. Наблюдаемую дифракционную картину можно объяснить с по­мощью построения зон Френеля. Разобьем открытую часть волновой поверх­ности на N элементарных зон ширины b/N. Каж­дая зона создает вторичные волны одинаковой амплитуды E0 / N. Если откры­тая часть волновой поверхности разбивается из точки наблюдения Р на четное число зон, то бу­дет минимум интенсивности, т.к. колебания от каждой пары соседних зон приходят в противофазе и взаимно гасят друг друга. Наоборот, если число зон будет нечетным, то результирующая интенсивность в точке наблю­дения будет максимальной, т.к. действие одной из зон окажется нескомпенсированным. Т.о., условие дифракционного минимума: b·sinφ=m·λ. Условие дифракционного максимума: b·sinφ=(2·m+1)λ/2. Дифракция Фраунгофера на дифракционной решеткеДифракционная решетка – это система из большого числа N параллель­ных друг другу щелей шириной b. Щели разделе­ны непрозрачными, равными по ширине, про­межутками а. Расстояние d = а + bназывается периодом решетки.Пусть плоская монохроматическая световая волна интенсивности I0 падает на решетку нор­мально. Колебания, исходящие от щелей, коге­рентны, они интерферируют друг с другом, и дифракционная картина состоит из достаточно узких интенсивных максимумов.В центр дифракционной картины (φ = 0) коге­рентные колебания от всех щелей приходят в фазе, поэтому наблюдается центральный максимум освещенности.Аналогичный резуль­тат получается и при углах дифракции φ, для кото­рых оптическая разность хода Δ колебаний от со­седних щелей равна целому числу длин волн:Δ=d·sinφ=m·λ. (m=0,1,2…) В направлениях φ, определяемых этим уравне­нием, возникают максимумы. Их называют глав­ными максимумами m-го порядка, а само урав­нение – у словием главных максимумов (рис. ).Из этой формулы следует, что лучи различной длины волны будут иметь максимумы в различ­ных направлениях. Если на дифракционную ре­шетку падает белый свет, то центральный мак­симум (φ = 0) будет представлять собой белую полосу. Во всех остальных порядках будет наблюдаться радужное цветовое размытие (сплошной спектр), обращенное к централь­ной белой полосе фиолетовым краем.С увеличением числа щелей растут интенсив­ность и резкость главных максимумов. Положение минимумов освещенности для дифракционной решетки определяется также, как и для одной щели: b·sinφ= m'·λ., где m' = 1,2,3... Разрешающая способность решетки по­казывает ее способность различать две очень близко расположенные линии в спектре и определяется формулой R=λ/Δλ,где Δλ – наименьшая разность длин волн двух соседних спектральных линий λ и λ+Δλ, при которой эти линии в спектре видны раздельно.Угловая дисперсия D определяет угловую ширину спектра D = dφ/dλ. Она численно равна угловому расстоянию dφ между двумя линиями спектра, длины волн которых различаются на единицу. Дифракция рентгеновских лучей. Для рентгеновских лучей в качестве дифракционной решетки можно использовать кристаллы, в которых расстояние между атомными плоскостями d сравнимо с длиной волны λ(λ

Формула Планка для испускательной способности АЧТ: точно согласуется с данными опытов и объясняет все экспериментальные законы теплового излучения тел. 3.4. ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА. ДАВЛЕНИЕ СВЕТА. Фотоэффект. Классическая теория, представляющая свет как электромагнитные волны, не смогла объяснить законы фотоэффекта и эффект Комптона. Явлением внешнего фотоэффекта назы­вается вырывание электронов с поверхности тела под действием света достаточно вы­сокой частоты. Экспериментально были установлены следующие закономерности внешнего фотоэффекта: Максимальная кинетическая энергия фотоэлектронов линейно растет с увеличением частоты света и не зависит от его интенсивности. Для каждого вещества существует т.н. «красная граница» фотоэффекта, т.е., наименьшая частота νМИН, при которой еще возможен фотоэффект. Число фотоэлектронов, вырываемых светом из катода за 1с, прямо пропорционально интенсивности света. Фотоэффект практически безынерционен, фототок возникает практически мгновенно после начала освещения катода при условии, что частота света ν ≥ νМИН . А.Эйнштейн пришел к выводу, что свет распространяется в пространстве и поглощается веществом в виде фотонов – квантов электромагнитного поля с энергией εf = hv.При взаимодействии с веществом фотон целиком передает свою энергию одному электрону. Эта энергия за­трачивается на работу выхода электрона из вещества АВЫХ и сообщение вылетевшему элект­рону кинетической энергии EКИН: (формула Эйнштейна).Это выражение объясняет все экспериментальные законы фотоэффекта. В частности, «красную границу» фотоэффекта, т.е., νМИН= АВЫХ/h. Кроме того, фототок прекращается, т.е. электроны не долетают до анода, при приложении между электродами т.н. задерживающей разности потенциалов . Эффект Комптона состоит в наблюдении у рассеянного на веществе рентгеновского излучения увеличения длины волны. Он не объясним с волновой точки зрения, т.к. согласно ей при прохождении электромагнитной волны через вещество возникает вторичное излучение с той же самой длиной волны. Этот эффект легко объясняется, если его рассматривать как упругое соударение двух частиц: фотона (f) и неподвижного электрона (e) (рассеяние фотона на электроне) и записать законы сохранения импульса и энергии: . Учтем, что энергия электрона после столкновения ; εf=hν=hc/λ и εf’=hν’=hc/λ’ – энергии налетающего и рассеянного фотонов, соответственно; θ – угол рассеяния, т.е. угол между векторами импульсов фотонов . Так как электромагнитная волна, обладаю­щая энергией Е, имеет импульс р = Е/c(это вытекает из общего выражения СТО для энергии при m= 0), то та­кое же соотношение должно выполняться и для импульса фотона:pf= εf/c = hv/c=h/λ=ħ·k, где λ и k=2π/λ - длина волны и модуль волнового вектора , соответственно, ħ=h/2π – тоже постоянная Планка.Решая совместно уравнения получим: , где – т.н. комптоновская длина волны для электрона.Рассматривая свет как поток частиц-фотонов удалось также объяснить давление света на поверхность. Давление света. Фотоны, обладая импульсами, попадая на поверхность, ока­зывают на нее давление. Если п – плотность фотонов, то на единицу поверхности в единицу времени попадает п·с фотонов. При поглощении каждый фотон сообщает поверхности импульс рf = hv/c, тогда все фотоны сообщат единице площади поверхности в единицу времени импульс (а это и есть давление): Р =(hv/c)· п·с= εf ·n. Но величина εf ·nравна энергии фотонов, за­ключенных в единице объема, т.е., объемной плотности электромагнитной энергии w. Таким образом, Р = wили с учетом того, что часть фотонов отражается: Р = w(1+ ρ), где ρ –коэффициент отражения, равный 1 при полном отражении фотонов, и 0 при их полном поглощении. Полученный результат совпадает с выражением для давле­ния света в электромагнитной теории. 3.5. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ. Корпускулярно-волновой дуа­лизм света. Т.о., в одних опытах (дифракция, интерференция, поляризация) свет проявляет волновые свойства, в других же (тепловое излучение, фотоэффект, эффект Комптона) он ведет себя как поток частиц-фотонов, но никогда не проявляет волновые и корпускулярные свойства одновременно. Волновая и квантовая теории света допол­няют друг друга. Двойственная природа света получила название корпускулярно-волнового дуа­лизма света и находит свое выражение в формулах, определяю­щих основные характеристики фотонов. Как видно из этих формул, корпускулярные характеристики фотона – энергия εf = hvиимпульс рf = hv/c=h/λ– связаны с волновыми характеристиками света : его частотой ν и длиной волны λ.Боль­шая группа оптических явлений – интерференция, дифракция, поляризация – полностью объясняется в волновой оптике. Однако, если «перемещаться» от длинных волн в сторону более коротких, то вол­новые свойства света будут проявляться все слабее, уступая место более отчетливо проявляющимся квантовым свойствам. Это видно, например, из существования «красной границы» фотоэффекта и такой же границы для фотохимических реакций. Р ассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллель­ный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, распо­ложенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E0·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропор­циональная интенсивности I(x) вэтой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)E(x) 2.С квантовой точки зрения образование на эк­ране дифракционной картины означает, что при прохождении све­та через щель происходит перераспределениефотонов в пространстве. В результате этого в разные точки экрана попадает различноечисло фотонов. Освещенность экрана в данной точке будет тем больше, чем большей будет суммарная энергия фотонов, попадающих за еди­ницу времени в данную точку. Эта энергия, в свою очередь, пропорциональна числу п(x) фотонов, доставивших эту энергию. Таким образом, I(x) п(x).Из сказанного следует, что E(x) 2

Второе соотношение устанавливает связь между неопределенностью энергии ΔE квазистационарного возбужденного состояния и средним временем жизни Δtвозбужденного состояния в атомных процессах. Например, достаточно точно можно измерить энергию системы в стационарном состоянии, время жизни в котором велико (Δt→ ∞), если же система находится в нестационарном состоянии, время жизни Δt в котором конечно, энергию можно измерить с погрешностью порядка ΔE


2.8. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ.

Если электрические и магнитные поля изме­няются во времени, то по отдельности их рас­сматривать уже нельзя: взаимное превраще­ние электрических и магнитных полей приводит к появлению электромагнитной волны.

Для среды – однородного и изотропного диэлектрика, не обладающего сегнетоэлектрическими или ферромагнитными свойствами, из уравнений Максвелла можно получить, что векторы напряженностей переменного электромагнитного поля удовлетворяют уравнениям: и , где - оператор Лапласа. Но это уравнения, описывающие волновой процесс, в которых скорость распространения волны определяется коэффициентом, стоящим перед второй производной по времени: Решением этих уравнений является т.н. плоская монохроматическая гармоническая волна: , , где - волновой вектор, указывающий направление распространения волны. Т.о., переменное электромагнитное поле действительно распространяется в пространстве в виде волн. Если волна распространяется в вакууме ( ), то . Этот результат в точности совпадает с изме­ренным значением скорости света с, что послу­жило основой для создания электромагнитной теории света.

Свойства электромагнитных волн

– Электромагнитные волны – поперечные волны; векторы и лежат в плоскости, перпендикулярной к скорости волны в данной точке поля.

– Векторы и взаимно перпендикулярны и образуют с направлением распространения волны, т.е. скоростью , правовинтовую систему (рис.).

– Взаимно перпендикулярные векторы и колеблются в одной фазе, причем мгновенные значения EиH связаны соотношением: , т.е. они д остигают максимума и обра­щаются в нуль в одних и тех же точках в одни и те же моменты времени.

– В вакууме скорость электромагнитной волны равна с и не зависит от частоты.

– Объемная плотность энергии электромаг­нитного поля складывается из объемных плотностей энергии электрического и магнитного полей: . С учетом соотношения, связывающего E и H, получим: .

– Направление распространения электромаг­нитной волны и энергию, переносимую волной в единицу времени через перпен­дикулярно ориентированную площадку единичной площади, опреде­ляет вектор Умова—Пойнтинга, аналогичный вектору Умова, введенному для механической волны,: . Среднее значение модуля этого вектора представляет интенсивность волны.

– Поскольку различные электромагнитные вол­ны имеют общую природу, их можно представить в виде единой шкалы.

Вся шкала условно подразделена на 6 диа­пазонов в порядке уменьшения длины волны (возрастания частоты) :

  1. радиоволны (длинные, средние и короткие) (от нескольких км до 0,1 мм);

  2. инфракрасное излучение (от 0, 1 мм до 0,74 мкм);

  3. видимое излучение (от 0,74 до 0,38 мкм);

  4. ультрафиолетовое излучение ( от 0,38 мкм до 1нм (10 - 9м ));

  5. рентгеновское излучение ( от 1 нм=10 Å до 0,1 Å (1Å=10 -10м ));

  6. гамма-излучение ( короче, чем 0,1Å).


Радиоволны обусловлены переменными то­ками в проводниках и электронными потоками. В инфракрасной, видимой и ультрафиолетовой областях излучают атомы, молекулы и быстрые заряженные частицы. Рентгеновское излучение возникает при внутриатомных процессах, γ-излучение имеет ядерное происхождение. Частич­но диапазоны перекрываются, т.к. волны одной и той же длины могут излучаться в разных про­цессах.
ФИЗИКА. Часть 3.


    1. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ СВЕТА .


Интерференция света

Пусть в произвольную точку наблюдения Р на экране Э приходят две волны (рис.): и ,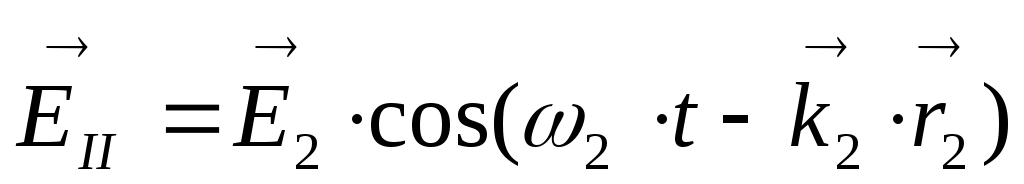

где ЕI и ЕII – напря­женности электри­ческих полей световых волн, идущих от источников S1 и S2 , ω1 и ω2 – частоты волн, 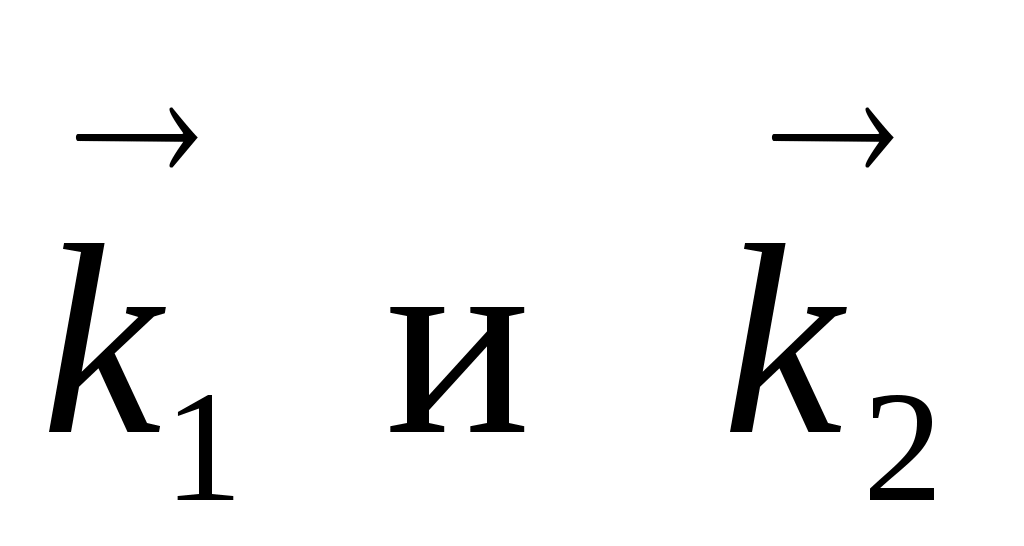-соответствующие волновые векторы. Сложение таких колебаний (можно применить формулу косинусов) дает: .

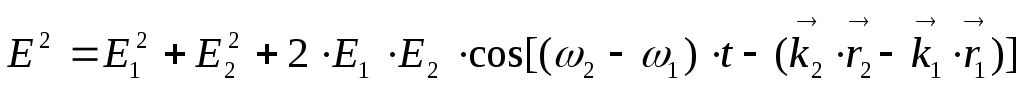Если учесть, что интенсивность волны пропорциональна квадрату амплитуды (I

Е
2), и обозначить разность фаз как , то получим для интенсивно­сти результирующей волны в точке Р:

.

Таким образом, результат сложения зависит от третьего слагаемого, которое называется интерференционным слагаемым. Здесь возможны два случая.

I. При наложении световых волн от двух независимых источников разность фаз ΔΦ за время наблюдения многократно изменяется случайным образом. Вследствие этого значение cosΔΦ, входящего в интерферен­ционное слагаемое, следует усреднить. Так как среднее за период значение косинуса равно нулю, то наблю­даемая в таких случаях интенсивность равна просто сумме интенсивностей двух волн , и наблюдается равномерная освещенность поверхности, на которую падают волны от источников. Такие волны называются некогерентными.

II. ΔΦ от времени не зависит. Это возможно лишь при наложении монохроматических волн (ω1 = ω2 = ω). Тогда . Здесь учтено, что волновое число и длина волны λ в среде с показателем преломления п связана с длиной волны λ0 в вакууме соотношением: λ=λ0/n . Выражение в круглых скобках Δ=n2·r2 – n1·r1– т.н. оптическая разность хода волн. В этом случае для точки Р на экране Э :

а) если cosΔΦ
= 1 , т.е. ΔΦ=m·2π и Δ=m·λ0 , то наблюдается максимум интенсивности . Амплитуды волн складываются: E = E1+E2 .

б) если cosΔΦ = –1 , т.е., ΔΦ=(2m+1)π и Δ=(2m+1)·λ0/2, то получается минимум интенсивности .Амплитуды волн вычитаются: E = E1 – E2 .

m – целое число, принимающее значения 0,1,2,…

Таким образом, в случае II образу­ется устойчивая картина усиления света в одних областях пространства и ослабления в других. Это свойство световых потоков непосред­ственно указывает на их волновую природу: две системы волн усиливают друг друга там, где максимумы и минимумы волн одной системы попадают на соответствующие максимумы и минимумы другой, и ослабляют друг друга, если максимумы одной волны накладываются на минимумы другой. Такая картина называется интерференционной , а само явление нало­жения волн, приводящее к перераспределению энергии в пространстве, –интерференцией света .

Когерентность. Для возникновения интерференции волн необходимо, чтобы волны имели одинаковую частоту и разность фаз колебаний полей в этих волнах оставалась постоянной во времени. В этом случае интерференционная картина не размывается со временем и не перемещается в пространстве. Волны, удовлетворяющие указанным условиям, называются когерентными. Самый простой способ получения когерентных волн - расщепление волны от какого-то монохроматического источника на две или несколько волн (эти волны будут когерентны
, если при расщеплении, например, при отражении от зеркала, не вносится неконтролируемая разность фаз).


Интерференция в тонких пленках.

Этот тип интерференции знаком всем по радужным разводам, появляющимся, если пролить каплю бензина на поверхность воды. Растекаясь по поверхности, бензин образует тонкую пленку. Падающий свет отражается как от верхней, так и от нижней поверхности тонкой пленки, создавая когерентные отраженные лучи с определенной разностью хода. В результате наблюдается интерференционная картина, состоящая из светлых и темных полос (для монохроматического света) или из радужных полос (для естественного дневного света).

Пусть пучок света падает на плоскопараллель­ную пластинку (рис.). Луч 1 в точке А испытыва­ет отражение (луч 2) и преломление (луч AM). Преломленный луч отражается от нижней грани и, вторично преломившись в точке В, выходит из пластинки (луч 3) параллельно лучу 2. Лучи 2 и 3 когерентны и будут интерферировать. Оптическая разность хода лучей 2 и 3 опре­деляется выражением .

З 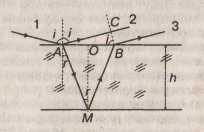десь учтено, что луч 2 отражается от грани­цы раздела со средой, оптически более плотной (с большим показателем преломления), при этом фаза волны изменяется на π, а следова­тельно, оптическая разность хода увеличивает­ся на λ / 2.Выразив cosr по закону преломления через угол падения i и показатель преломления среды п, получим:

.

Тогда максимум интерференции наблюдает­ся, если

,а условием минимума будет

, где m =1,2,3,…

В результате, если на пластинку падает моно­хроматическое излучение, то она будет выгля­деть яркой или темной в зависимости от того, будут волны усиливаться или ослабляться. При
освещении белым светом условия минимума и максимума будут выполняться для отдельных волн, и пластинка станет окрашенной. Каждой из полос соответствует определенное значение угла падения i. Поэтому они называются поло­сами, или линиями, равного наклона.

При падении монохроматического света на пластинку переменной толщины (клин) каждому значению hсоответствует свое условие интер­ференции, поэтому пластинка пересечена свет­лыми и темными полосами равной толщины. Интерференционные полосы в этом случае ло­кализованы на поверхности клина.

Приведенные выше формулы соответствуют интер­ференции в отраженном свете. Если наблюде­ние ведется в тонких пластинках или пленках, находящихся в воздухе, на просвет (в проходя­щем свете), то потери волны при отражении не произойдет. Следовательно, оптические разно­сти хода для проходящего и отраженного света отличаются на λ/2, т.е. максимумам интерфе­ренции в отраженном свете соответствуют ми­нимумы в проходящем свете и наоборот.

Смотрите также файлы