Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 369
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
V (см. уравнение (4)). Расширяясь, газ производит работу. Пусть в цилиндре поршень площадью S под действием постоянной силы F передвинулся вследствие расширения газа на расстояние dx. Работа газа будет равна:
δA = F·dx= p·S·dx= p·dV(20).
Если Fизменяется, то: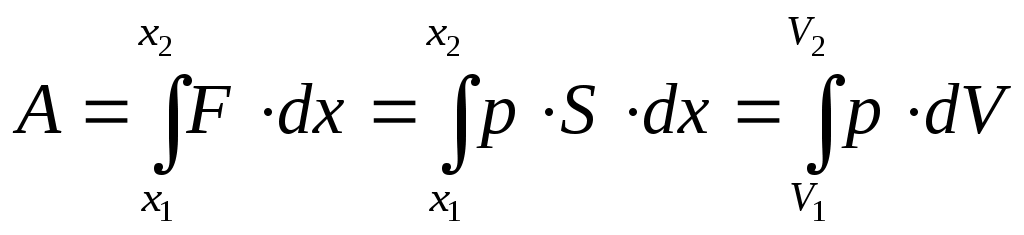 (21).
(21).
На рис.б p·dV– это площадь заштрихованной полоски, a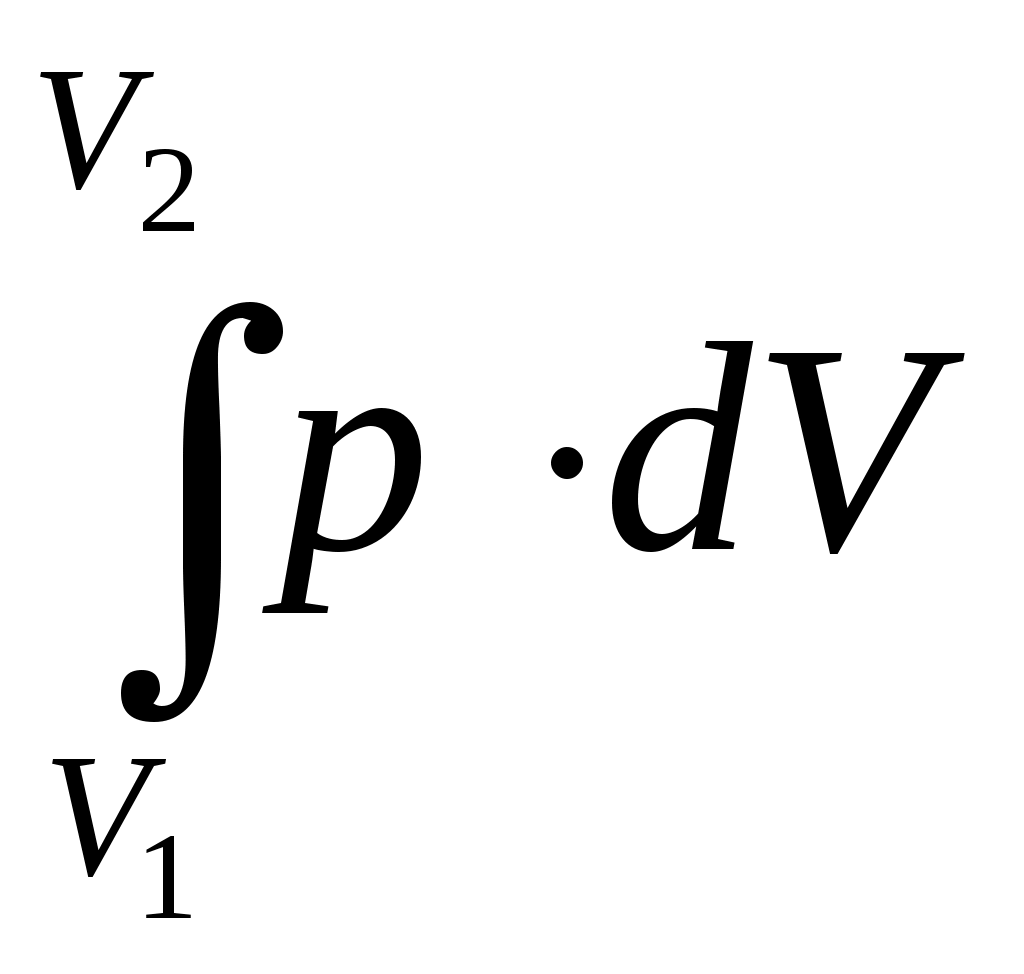 – это сумма площадей всех полосок от V1 до V2. T. о., работа газа измеряется площадью под кривой на диаграмме p–V.Очевидно, что работа зависит от процесса, т. е. от того, происходит ли расширение газа по кривой I или по кривой II (видно, что на рис. б под кривой II площадь больше, чем под кривой I).
– это сумма площадей всех полосок от V1 до V2. T. о., работа газа измеряется площадью под кривой на диаграмме p–V.Очевидно, что работа зависит от процесса, т. е. от того, происходит ли расширение газа по кривой I или по кривой II (видно, что на рис. б под кривой II площадь больше, чем под кривой I).
При изобарическом процессе ( рис. а, кривая I) работа газа:
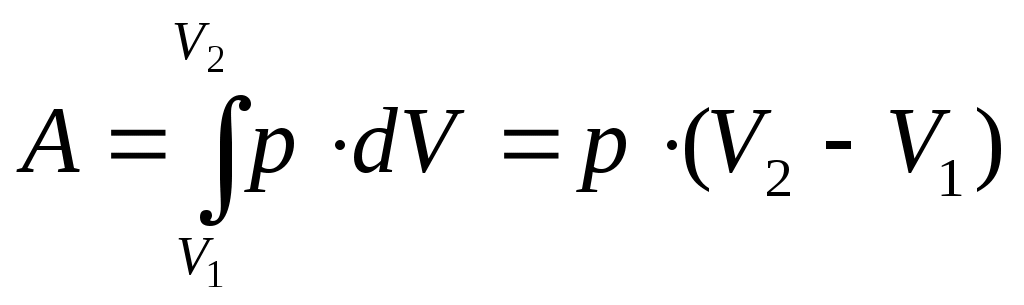 (22).
(22).
При изохорическом процессе ( рис. а, кривая II) объем не меняется, т. е. dV= 0 и, следовательно, А = 0. При изотермическом процессе меняются и р, и V ( рис. б). Заменив давление через объем и температуру, согласно уравнению (4), получим работу газа при T=const :
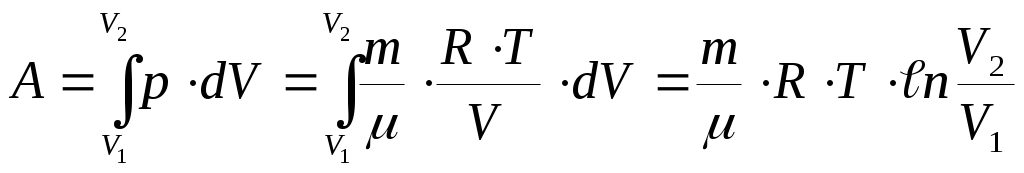 (23).
(23).
Проведем процесс расширения газа из состояния 1 (рис. б) в состояние 2 по кривой II (А>0), а сжатие обратно в состояние 1 – по кривой I (А<0). Процесс с возвращением в ту же точку называется циклом. Тогда общая работа будет равна разности площадей под кривыми II и I, т. е. площади цикла.
Если цикл на диаграммах p–V совершается по часовой стрелке (см. рис. б), то работа при расширении больше, чем при сжатии и полная работа А > 0. Поскольку мы возвращаемся в ту же точку, ΔU = 0. Из (18) следует, что при таком процессе и теплота, подводимая к телу, должна быть больше нуля (Q> 0). Так происходит в тепловой машине, когда тепло подводится, а машина производит положительную работу.
Если же цикл совершается против часовой стрелки, то А < 0. Соответственно и Q < 0, т. е. энергия не подводится к телу, а отводится от него. Это имеет место в холодильнике.
В обоих случаях происходит обмен энергией с окружающей средой либо в виде работы, либо в виде обмена теплотой.
Теплоемкость. Молярная теплоемкость газа. Степени свободы.
Под теплоемкостью С телапонимают то количество тепла, которое надо сообщить телу, чтобы повысить его температуру на один градус Кельвина:
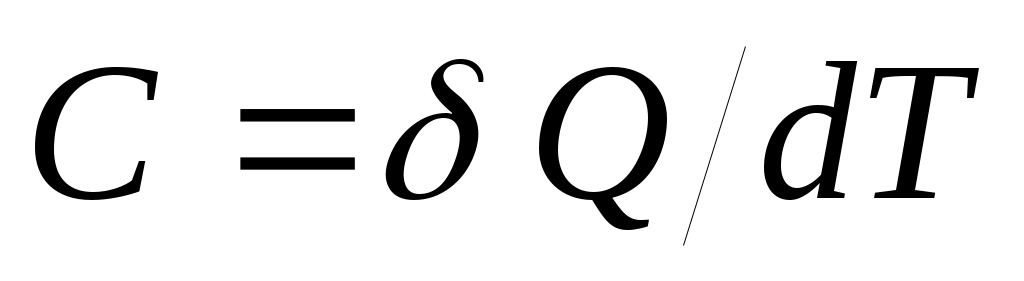 ( Дж/К ) (24)
( Дж/К ) (24)
Если передается энергия не всему телу, а одному килограмму, то говорят об удельной теплоемкости с = С/m( Дж/(кг·К)). Если речь идет об одном моле, то говорят омолярной теплоемкости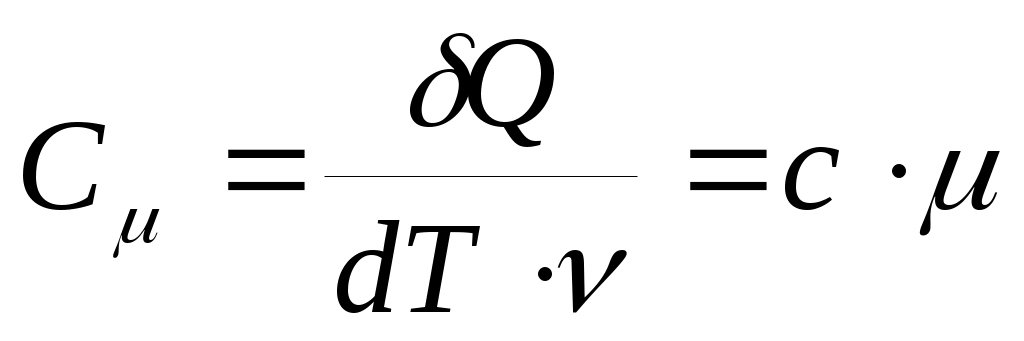 , измеряемой в Дж/(моль·К). О ней мы и будем говорить далее.
, измеряемой в Дж/(моль·К). О ней мы и будем говорить далее.
Поскольку при переходе тела из одного состояния в другое δQзависит от процесса, по которому производится этот переход, теплоемкость тоже зависит от процесса. Если процесс изохорический (V = const), то теплоемкость обозначается СV. Если процесс изобарический, то – Ср. При изотермическом процессе dT = 0, a δQне равно нулю и соответствующая теплоемкость устремляется к бесконечности СТ → ∞.
Определим СV (теплоемкость 1 моля при постоянном объеме), использовав первое начало термодинамики в дифференциальной форме (19).
Поскольку V = const, тоdV = 0 и δA= 0 и для СVполучаем:
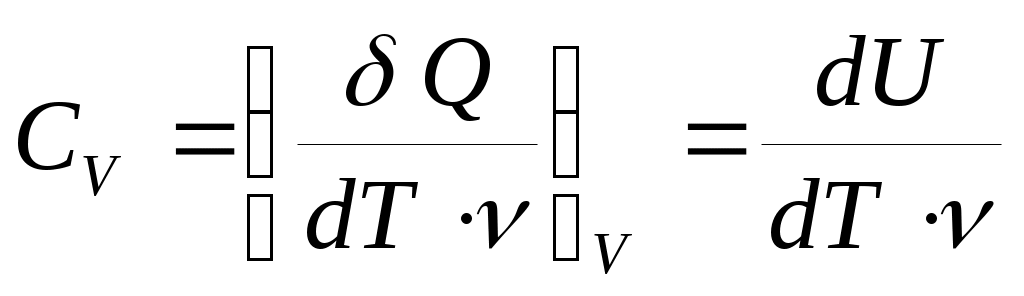 (25) .
(25) .
Значок вне скобок указывает на тип процесса, т. е. что V= const. Соотношение (25) означает, что при постоянном объеме все подводимое тепло идет только на изменение внутренней энергии U.
При изобарическом процессе (р = const), для теплоемкости Ср получаем:
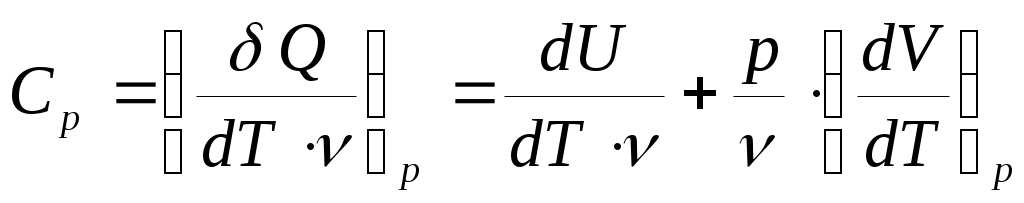 (26).
(26).
Найдем (dV/dT)pиз уравнения Клапейрона (4):
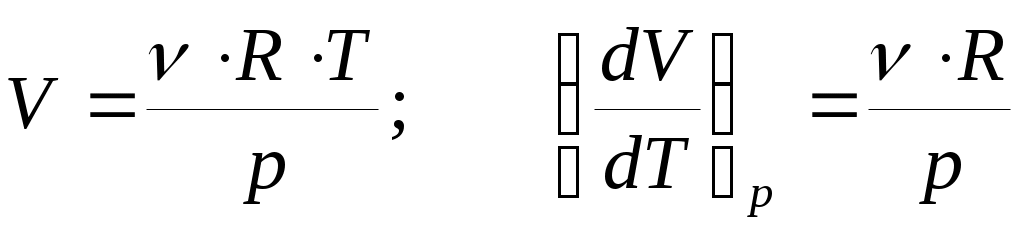 (27)
(27)
и подставив в (26), получим уравнение Майера: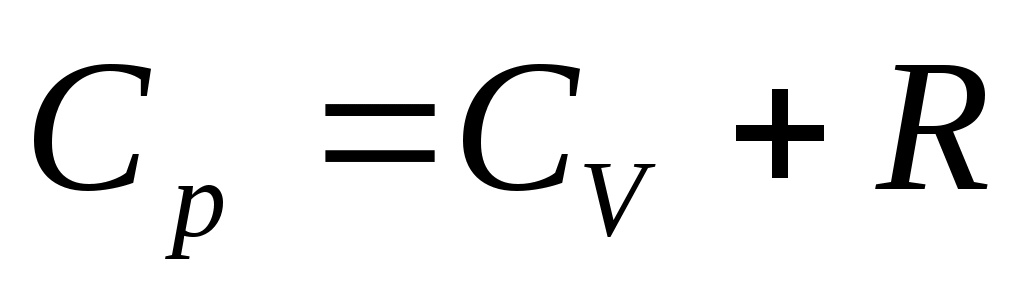 (28).
(28).
Cp больше, чем СV , так как подведенная теплота идет не только на увеличение внутренней энергии, но и на работу расширения газа.
Определим dU/dT, так как эта производная входит в (25) и (26). Для идеального газа внутренняя энергия равна сумме средних кинетических энергий всех N молекул: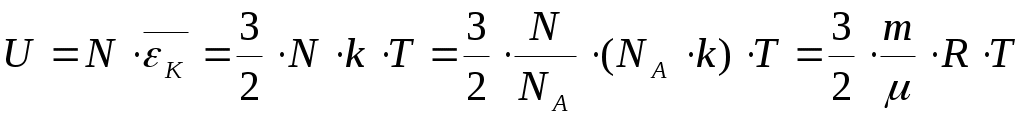 (29). Тогда
(29). Тогда 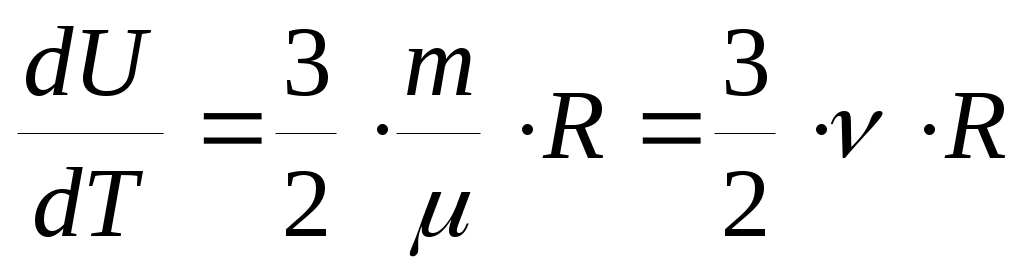 ;
; 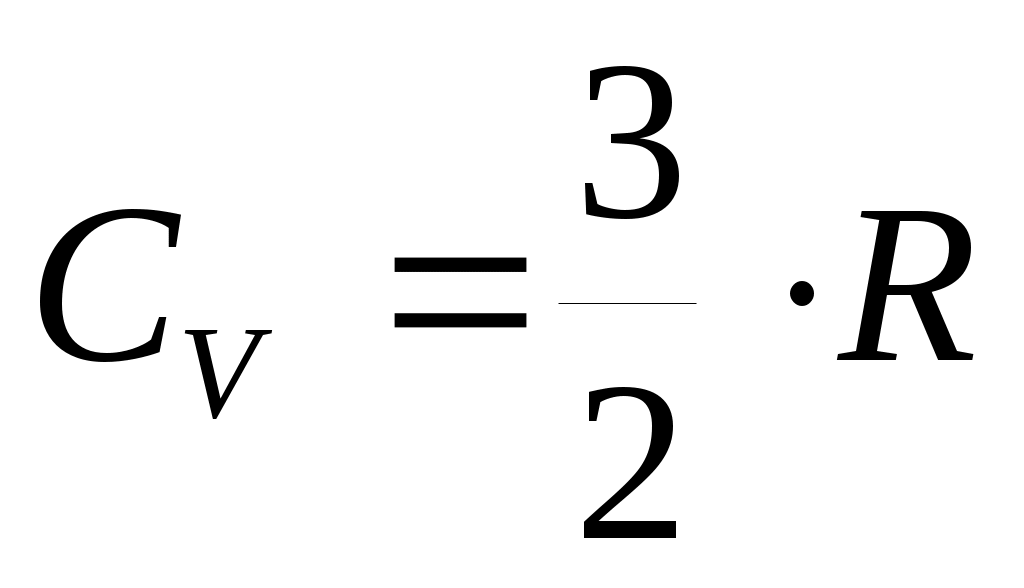 ;
; 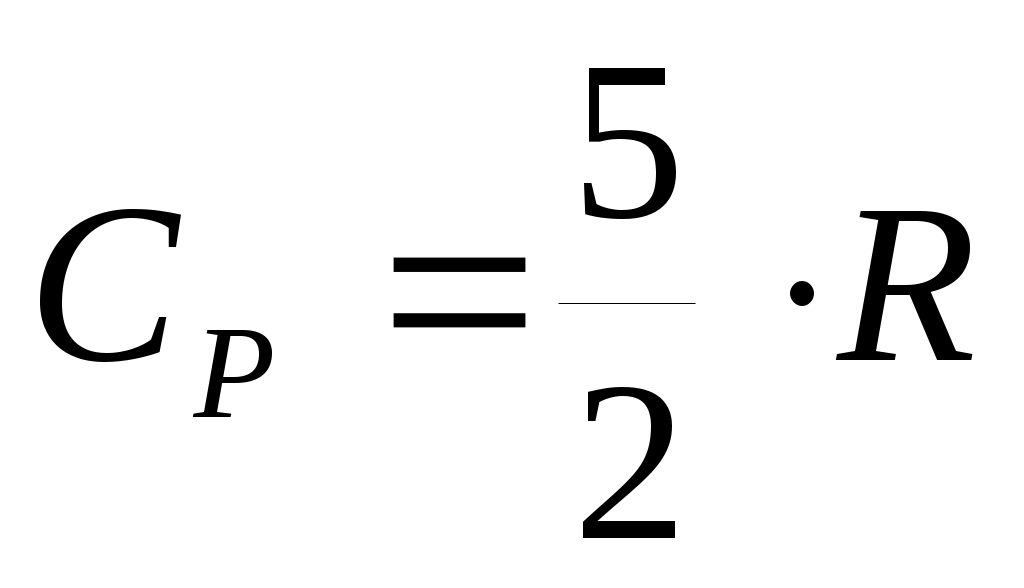 (30). В выражении для
(30). В выражении для 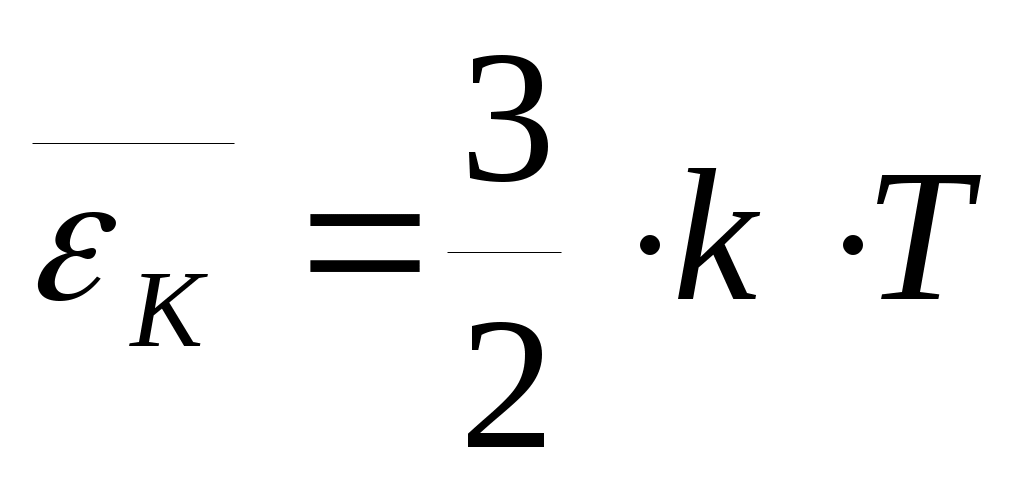 учитывалась только кинетическая энергия поступательного движения в трехмерном пространстве. Число независимых координат, необходимых, чтобы полностью определить положение тела в пространстве, называется числом степеней свободы i. Будем считать атомы, из которых состоит молекула, материальными точками, тогда одноатомная молекула имеет три степени свободы поступательного движения i= 3. И т.о., на каждую степень свободы приходится энергия по (1/2)kТ.
учитывалась только кинетическая энергия поступательного движения в трехмерном пространстве. Число независимых координат, необходимых, чтобы полностью определить положение тела в пространстве, называется числом степеней свободы i. Будем считать атомы, из которых состоит молекула, материальными точками, тогда одноатомная молекула имеет три степени свободы поступательного движения i= 3. И т.о., на каждую степень свободы приходится энергия по (1/2)kТ.
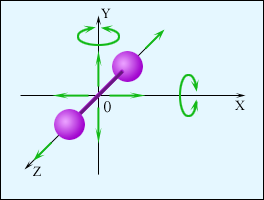 Если молекула двухатомная (рис.), то, кроме поступательного движения, она может еще вращаться вокруг осей xи y.
Если молекула двухатомная (рис.), то, кроме поступательного движения, она может еще вращаться вокруг осей xи y.
Вращение вокруг оси zне дает вклада в энергию, так как энергия вращательного движения равна J·ω2/2 = m·r2·ω2/2, а двухатомная молекула не имеет пространственной протяженности вдоль осей xи y.
Надо не только задать три координаты, чтобы определить положение центра масс молекулы в пространстве, но и задать еще две (вращательные) координаты, чтобы определить ее ориентацию в пространстве. Т.о., число степеней свободы для двухатомной молекулы i = 5.
Для трех- и более атомной молекулы вклад в энергию даст и вращение вокруг оси z . Для них i= 6 .
Молекулы мы считали жесткими; колебательные степени свободы не
учитывались. Если их учесть, результат будет немного иной, но колебательные степени свободы становятся существенными только при высоких температурах.
Итак, для жестких молекул внутренняя энергия и молярные теплоемкости равны: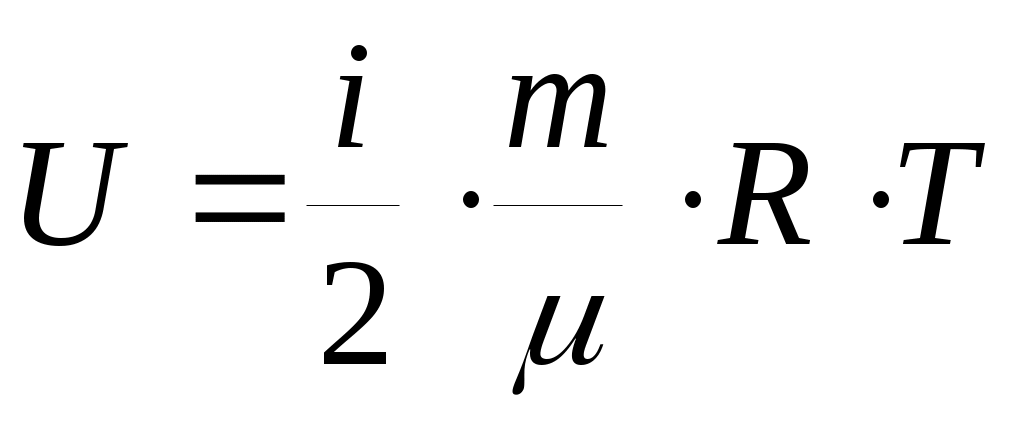 ;
; 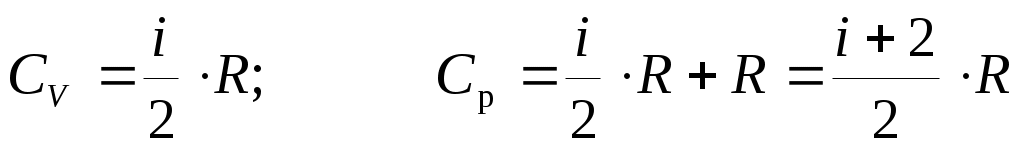 (31).
(31).
Все это сильно упрощенные рассуждения, непригодные, например, при очень низких или высоких температурах. Более последовательная теория теплоемкости строится на основе квантовой физики.
Адиабатический процесс
Процесс без обмена теплотой с окружающей средой называется адиабатическим. Он может происходить, если газ (или другое тело) окружен абсолютно не проводящей тепло оболочкой или процесс происходит очень быстро, так что газ не успевает обменяться теплом с другими телами.
При таких процессах первое начало термодинамики упрощается:
δQ = 0; dU = – δА. (32) .
Это означает, что если над газом производить работу (δА < 0), то dU > 0. Внутренняя энергия газа возрастает, он нагревается. Если же газ расширяется, то он сам производит работу δА > 0 за счет собственной внутренней энергии и dU < 0. В результате он охлаждается.
Согласно (25): dU=ν ·CV·dT. ДляδА используем соотношение (20). Тогда выражение (32) для адиабатического процесса можно записать так:
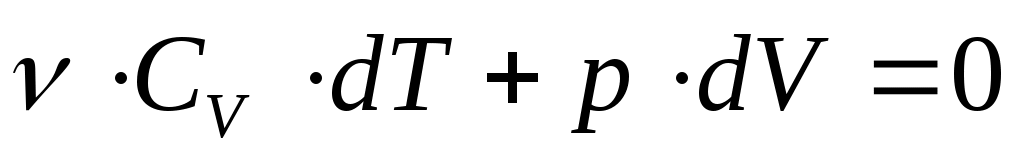 (33).
(33).
Подставим сюда р из уравнения Клапейрона-Менделеева (4) иполучим:
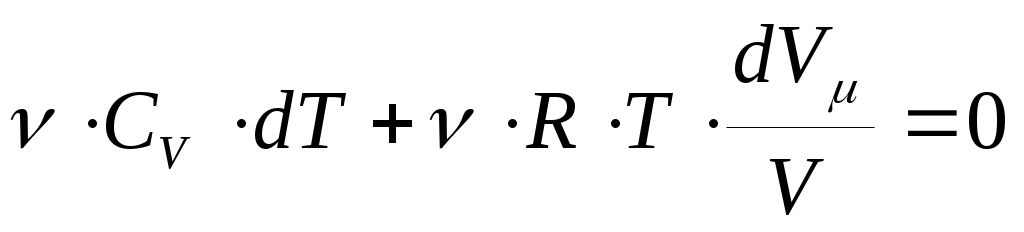 ;
; 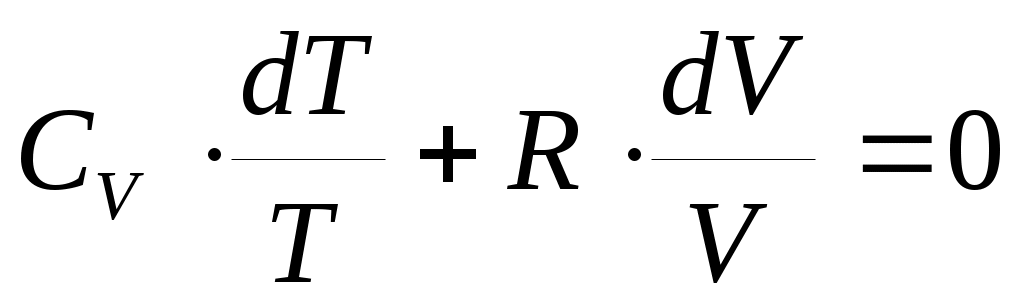 (34) .
(34) .
Проинтегрируем последнее выражение для пределов изменения переменных от T1 до T2 и от V1 до V2 и введя обозначение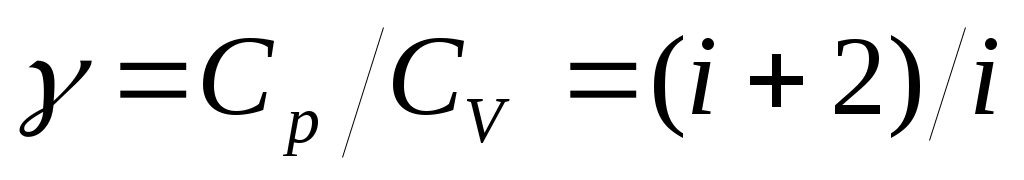 (35) . получим:
(35) . получим: 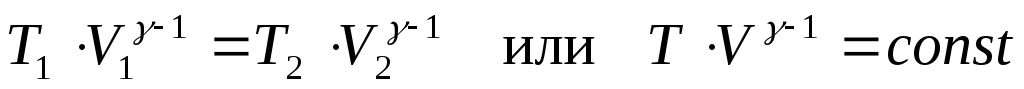 (36),
(36),
а используя Т = p·V/(ν·R) , получаем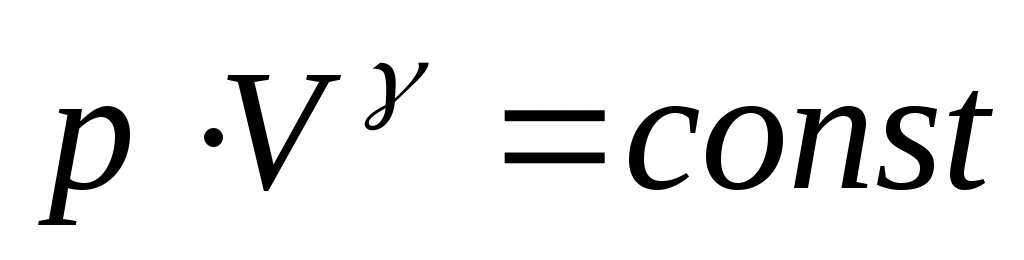 (37).
(37).
Соотношения (36-37) носят название уравнений Пуассона или адиабаты. γ – показатель адиабаты.
П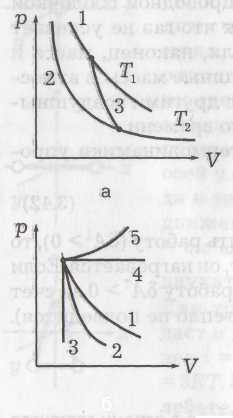 оскольку γ > 1, давление в (37) обратно пропорционально не
оскольку γ > 1, давление в (37) обратно пропорционально не
V, как было при изотермическом процессе, а Vγ, т. е. давление убывает с увеличением объема быстрее. На рисунке a кривые 1 и 2 – изотермы (Т2 < T1), а кривая 3 – адиабата.
При любых других процессах (неизотермических и неадиабатических) всегда можно связь между р и V написать в виде (37), но γ уже не будет равна Ср/СV .
В этих случаях процесс называется политропическим, а γ – показателем политропы.
Можно сказать, что для изотермического (T=const) процесса γ = 1, для изобарического (р = const) γ = 0, для изохорического (V = const) γ = ∞. На рисунке б показаны различные процессы расширения газа: 1 – изотерма, 2 – адиабата, 3 – изохора, 4 – изобара, 5 – политропа. Процессы 2, 3 идут с охлаждением, а 4, 5 – с нагреванием газа.
Круговые процессы (циклы). Цикл Карно
Газ, получая тепло и расширяясь, производит работу. Для непрерывного получения работы нужно, чтобы рабочее тело все время возвращалось в исходное состояние и снова повторялся тот же процесс, т. е. чтобы процесс был круговым, циклическим. При этом какую-то работу надо совершать над газом, сжимая его и возвращая в исходное состояние. Для того, чтобы тепловая машина совершала положительную работу необходимо, чтобы расширение газа происходило при более высоком давлении, чем сжатие. Это возможно, если при расширении в систему будет поступать энергия Q1 извне, например, от нагревателя, а при сжатии энергия Q2 должна быть отдана внешней среде – холодильнику.
После совершения цикла мы возвращаемся в исходное состояние с той же внутренней энергией. Следовательно, Δ
U = 0, а подведенное тепло Q1, за вычетом отдаваемого холодильнику Q2, переходит в полезную работу A=Q1 – Q2. Для оценки эффективности работы вводят коэффициент полезного действия (кпд) тепловой машины: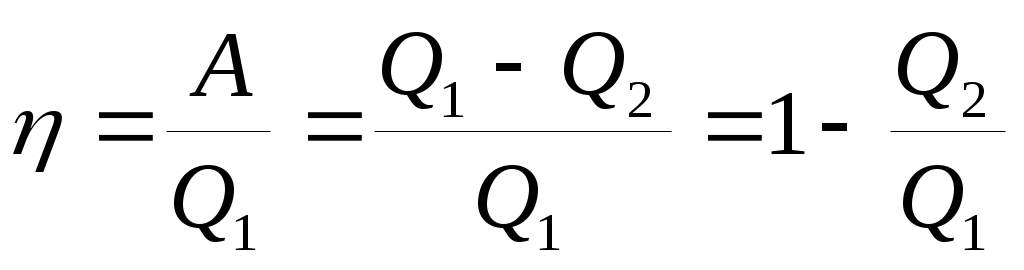 (38) .
(38) .
Работа машины тем эффективнее, чем больше можно получить от нее работы Aи чем меньше надо подводить тепла от нагревателяQ1.
Как показал С.Карно, максимальный кпд получается для цикла, состоящего из двух изотерм и двух адиабат (т.н. цикл Карно) (рис.) Газ расширяется из точки 1 в точку 2 по изотерме при температуре Т1 . При этом в уравнении (19) ΔU= 0, работа расширения газа A > 0, т.е., к газу должна подводиться энергия от нагревателя Q1 > 0.
П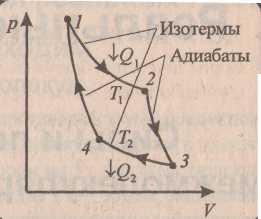 ри расширении по адиабате из точки 2 в точку 3 обмен теплотой равен нулю и работа расширения А производится за счет изменения внутренней энергии ΔU (газ охлаждается). Далее, внешние силы сжимают газ по изотерме 3 → 4 при температуре Т2. Здесь опять ΔU= 0, и из (19) следует, что А < 0, Q2 < 0. Чтобы произвести изотермическое сжатие, надо отводить тепло, отдавать его более холодному телу – холодильнику. Далее внешние силы сжимают газ по адиабате 4 → 1, возвращая газ в первоначальное состояние.
ри расширении по адиабате из точки 2 в точку 3 обмен теплотой равен нулю и работа расширения А производится за счет изменения внутренней энергии ΔU (газ охлаждается). Далее, внешние силы сжимают газ по изотерме 3 → 4 при температуре Т2. Здесь опять ΔU= 0, и из (19) следует, что А < 0, Q2 < 0. Чтобы произвести изотермическое сжатие, надо отводить тепло, отдавать его более холодному телу – холодильнику. Далее внешние силы сжимают газ по адиабате 4 → 1, возвращая газ в первоначальное состояние.
Пользуясь формулами (23), (36) и (38), можно получить для рассматриваемого цикла Карно :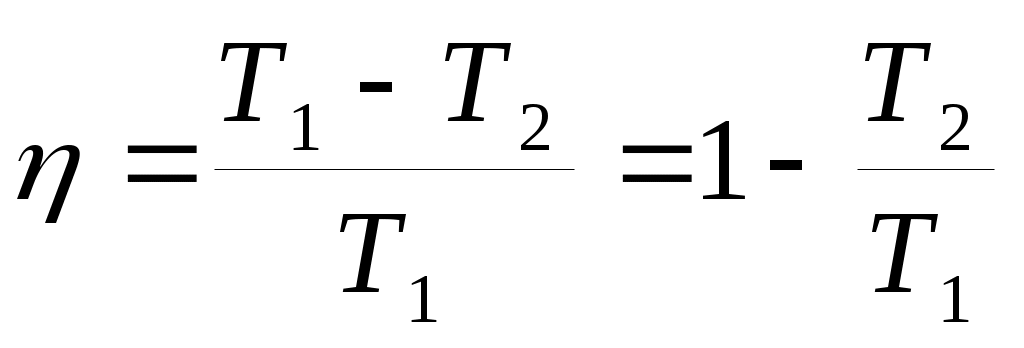 (39).
(39).
Из (39) следует, что кпд η тем больше, чем выше температура нагревателя Т1 и чем ниже температура холодильника Т2 .
Необратимые процессы
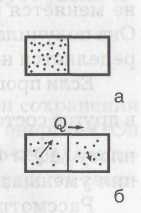 Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.
Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.
Другой пример: пусть газ находится и слева и справа от теплопроводной перегородки, но температура слева выше, чем температура справа (рис. б). Молекулы обмениваются с перегородкой кинетической энергией, и постепенно температуры обеих частей выравниваются. Такой процесс передачи тепла всегда необратим. Самопроизвольно средняя кинетическая энергия молекул (т. е. температура) слева сама не поднимется за счет кинетической энергии молекул справа.
Любой процесс, сопровождающийся трением, также необратим, так как при этом энергия упорядоченного движения переходит в энергию беспорядочного движения молекул, т. е. в теплоту.
Энтропия
Пусть с рабочим веществом совершаются циклы, при каждом из которых подводится от нагревателя Q1, отдается холодильнику Q2 и производится работа
А = Q1 – Q2 . Из (38) и (39) можно получить:
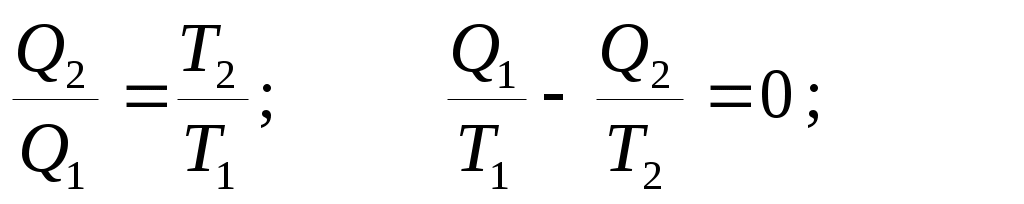 (40).
(40).
Величина Qi /Tiназывается приведенной теплотой. Обозначим ее ΔSi . Из (40) следует, что сумма приведенных теплот при циклическом процессе равна нулю. Это означает, что, какой бы циклический процесс мы ни совершали, если мы вернулись в исходное состояние, некоторая величина Sне меняется (ΔS = 0). Следовательно, S– функция состояния. Она получила название энтропии. Таким образом, состояние определяется не только внутренней энергией U, но и энтропией S. Если процесс не циклический и тело переходит из состояния 1 в другое состояние 2, то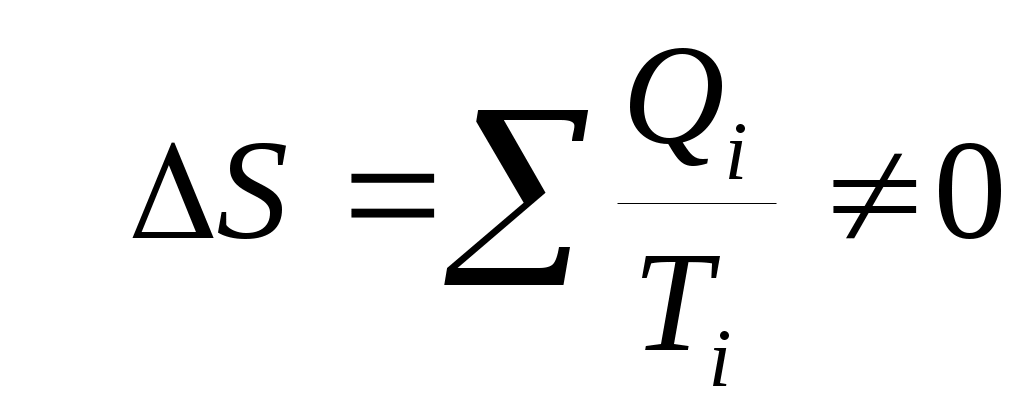 . Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q< 0) – энтропия уменьшается. При адиабатическом процессе (Q= 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным.
. Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q< 0) – энтропия уменьшается. При адиабатическом процессе (Q= 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным.
Рассмотрим теплопередачу при контакте двух тел при температурах Т1 и Т2 (Т1 > Т2) в теплоизолированной системе. ТеплотаQ, передаваемая телом 1, равна теплотеQ, полученной телом 2. Однако, тело 1 отдает ее при температуре Т1 и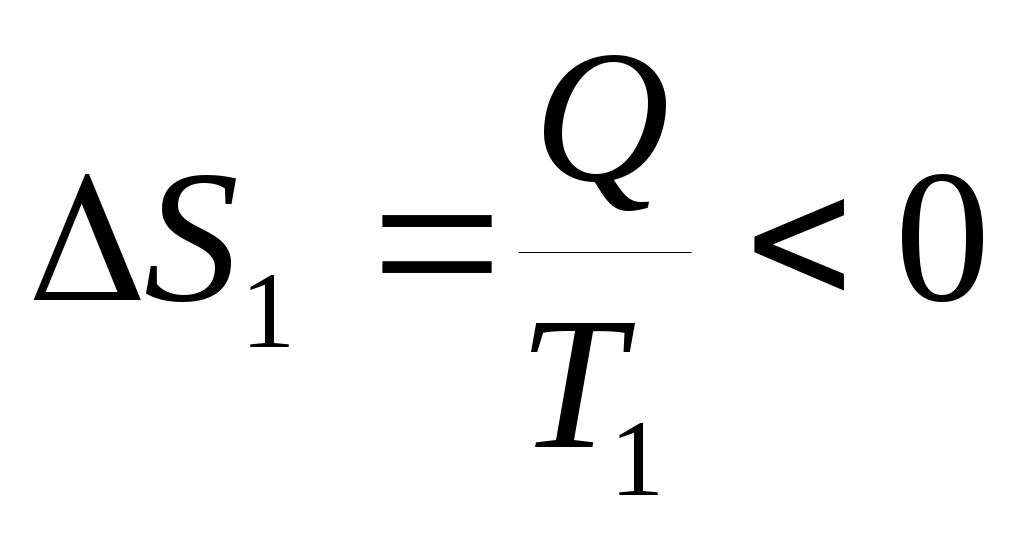 , а тело 2 получает ее при температуре Т2 и
, а тело 2 получает ее при температуре Т2 и 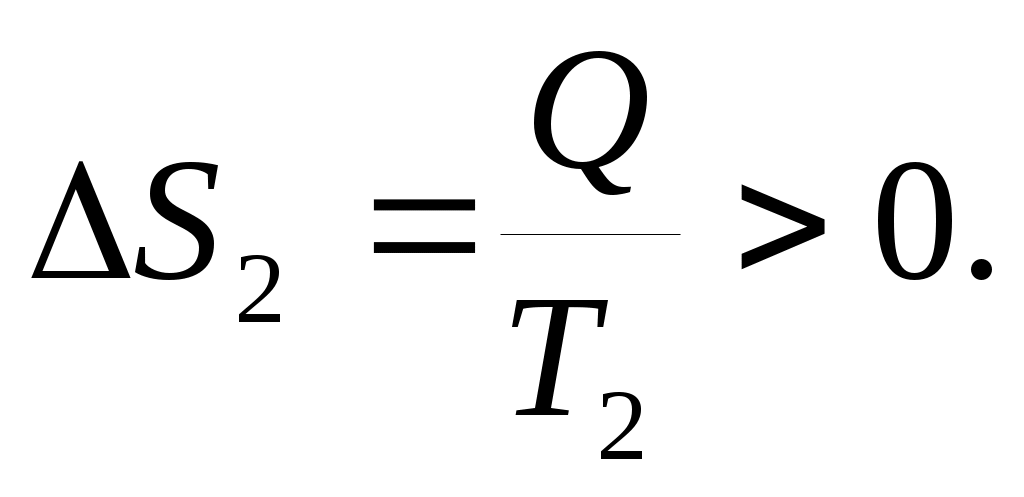 Так как Т1 > T2 , следовательно, │ΔS2│>│ΔS1│, так что в целом при таком процессе энтропия возрастает. Т.о., при необратимых процессах энтропия увеличивается.
Так как Т1 > T2 , следовательно, │ΔS2│>│ΔS1│, так что в целом при таком процессе энтропия возрастает. Т.о., при необратимых процессах энтропия увеличивается.
В тепловой машине часть теплоты, взятой от нагревателя, преобразуется в работу, а другая часть должна быть передана холодильнику. Нагреватель охлаждается, а холодильник нагревается.
С одной стороны, мы знаем, что при этом энтропия возрастает. С другой стороны, к.п.д. такой тепловой машины будет постепенно падать, так как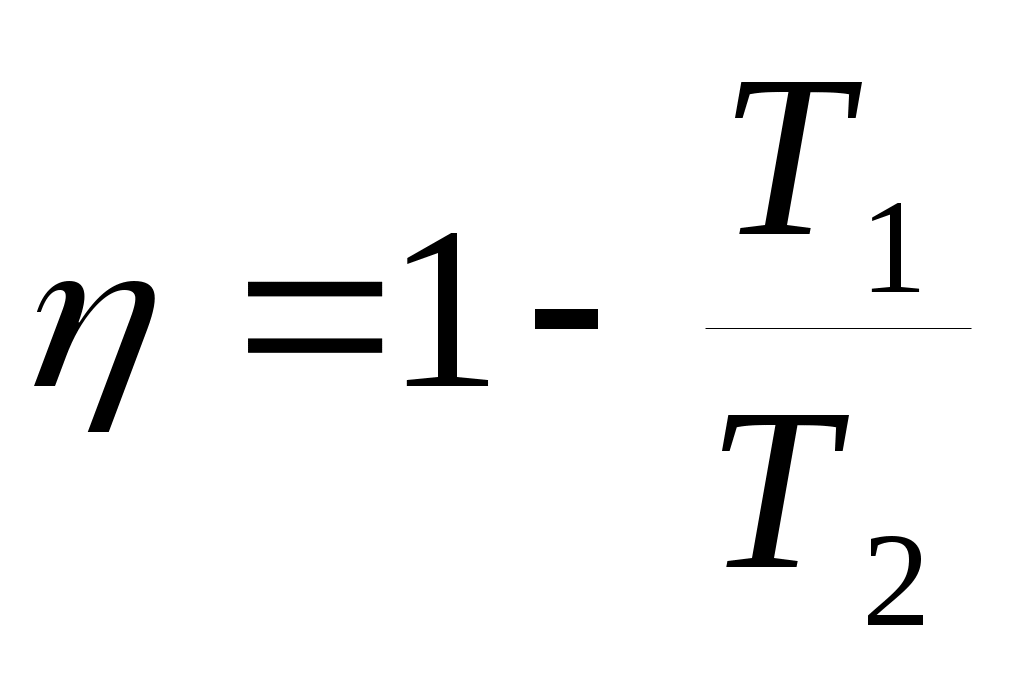 и при Т1 → T2 к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, остается неизменной, но работы получается все меньше и меньше. В пределе, когда Т1 = T2 , теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагревателя становится бесполезной. Таким образом, возрастание энтропии соответствует обесцениванию энергии.
и при Т1 → T2 к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, остается неизменной, но работы получается все меньше и меньше. В пределе, когда Т1 = T2 , теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагревателя становится бесполезной. Таким образом, возрастание энтропии соответствует обесцениванию энергии.
Энтропию можно связать со степенью упорядоченности системы. Увеличение энтропии соответствует увеличению беспорядка. Энтропия – это мера беспорядка. В наших примерах (рис.) система переходила из менее вероятного, упорядоченного, неравновесного состояния в более вероятное, неупорядоченное, равновесное.
Вычислим изменение энтропии для идеального газа, исходя из дифференциальных выражений для изменения энтропии и I начала термодинамики:
dS=δQ / T ;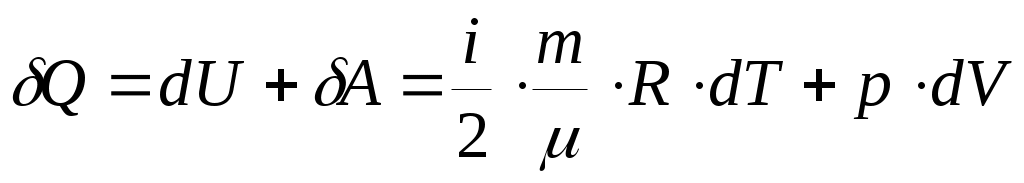 (41)
(41)
Учитывая, согласно уравнению Клапейрона , что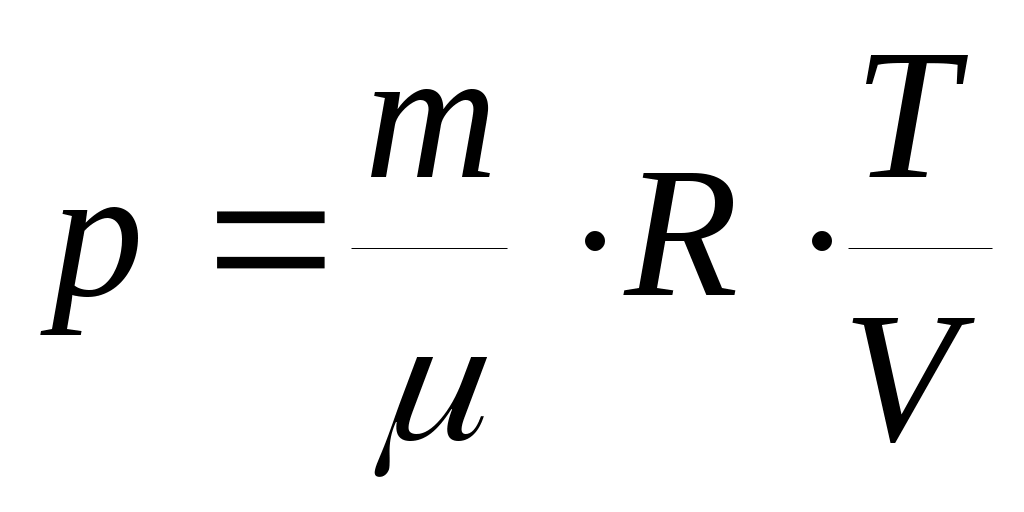 , и подставив p в δQ, а δQ в выражение для dS, получим :
, и подставив p в δQ, а δQ в выражение для dS, получим :
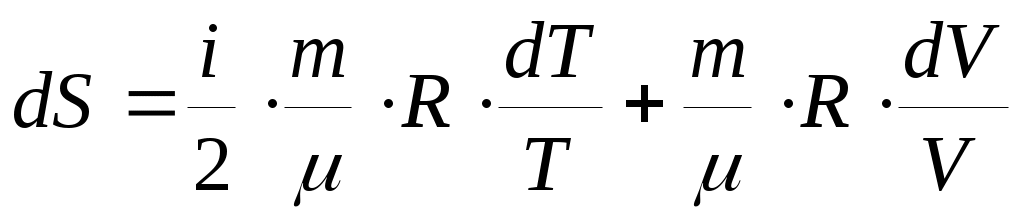 , которое после интегрирования определяет изменение энтропии идеального газа при переходе от состояния 1 с Т1 и V1 к состоянию 2 с Т2 и V2 :
, которое после интегрирования определяет изменение энтропии идеального газа при переходе от состояния 1 с Т1 и V1 к состоянию 2 с Т2 и V2 : 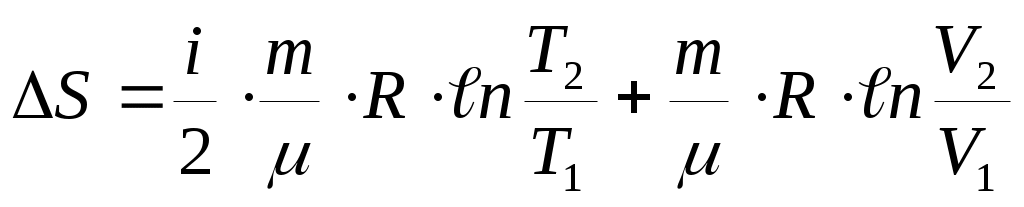 (42).
(42).
Второе начало термодинамики
Первое начало термодинамики (19, 41), т. е. закон сохранения энергии, справедливо при любом процессе обмена энергией. Оно не указывает направление процесса, для него неважно, будет ли тепло передаваться от горячего тела к холодному или наоборот, будет ли газ самопроизвольно расширяться или сжиматься и т. д..
Однако из рассмотренного выше вытекает, что:
1. Любая система, выведенная из состояния равновесия и предоставленная самой себе, возвращается в равновесное состояние. Таковы, например, необратимые процессы переноса: вещества (диффузия), энергии (теплопроводность), импульса упорядоченного движения (внутреннее трение или вязкость).
2. Механическая работа может быть полностью превращена в теплоту, т. е. энергия упорядоченного движения может полностью перейти в энергию неупорядоченного движения. Однако, энергия неупорядоченного движения (теплота) может быть преобразована в энергию упорядоченного движения (работу) лишь частично. Невозможен процесс, единственным результатом которого было бы полное превращение теплоты в работу. Т.е., кпд тепловой машины η < 1 .
3. Предоставленная самой себе система всегда переходит из менее вероятного в более вероятное состояние. Больцман получил соотношение, связывающее изменение энтропии при необратимых процессах с термодинамическими вероятностями (числом способов реализации того или иного состояния) начального W1 и конечного W2 состояний : ΔS=k·ℓn(W2/W1) . Из этого соотношения вытекает, что процессы с уменьшением энтропии не невозможны, а настолько маловероятны, что практически никогда не реализуются.
Используя понятие энтропии, можно сформулировать еще одно равносильное утверждение: «В замкнутой, изолированной системе (системе с постоянной энергией) при любых процессах энтропия не может убывать , т.е. ΔS≥0 ».
Все эти формулировки эквивалентны. Все они указывают направление процессов в изолированной или что то же самое в предоставленной самой себе системе. Это и есть второе начало термодинамики – важнейший закон природы.
Не следует думать, что этот закон вообще запрещает передачу тепла от холодного тела к нагретому. Это возможно, но только в незамкнутой (открытой) системе. Например, это осуществляется в холодильнике. Можно также уменьшить энтропию системы, например поршнем сжать газ и снова собрать его в одной половине сосуда. Можно увеличить порядок в системе (т. е. уменьшить энтропию), но для этого необходимо вмешательство внешних сил.
ФИЗИКА. Часть 2.
2.1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
Электрический заряд
В основе разнообразия явлений природы лежат четыре фундаментальных взаимодействия между элементарными частицами – сильное, электромагнитное, слабое и гравитационное. Каждое взаимодействие связывается с определенной характеристикой частицы. Например, гравитационное взаимодействие зависит от масс частиц, электромагнитное – от электрических зарядов и т. д.
Электрический заряд частицы является одной из основных, первичных ее характеристик. Ему присущи следующие фундаментальные свойства:
– дискретность: существует минимальный заряд, равный 1,6.10-19Кл; – двузначность: существуют положительные и отрицательные заряды; – инвариантность относительно преобразований Лоренца: величина заряда остаётся неизменной независимо от того, движется он или покоится; – сохранение заряда в изолированной системе: полный заряд электрически изолированной системы остаётся постоянным.
Заряд называется точечным, если можно пренебречь размерами заряженного тела по сравнению с расстоянием от этого тела до других зарядов. Любое заряженное тело можно рассматривать как совокупность точечных зарядов.
δA = F·dx= p·S·dx= p·dV(20).
Если Fизменяется, то:
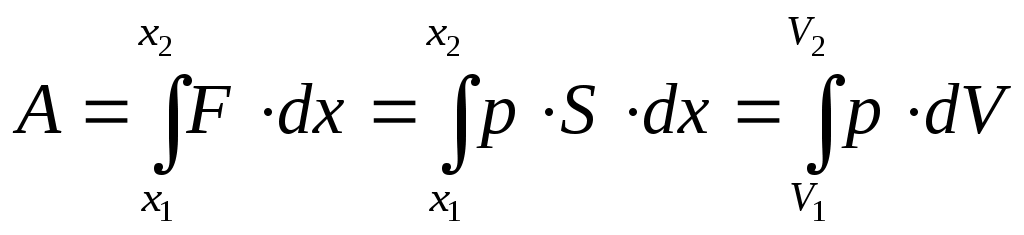 (21).
(21). На рис.б p·dV– это площадь заштрихованной полоски, a
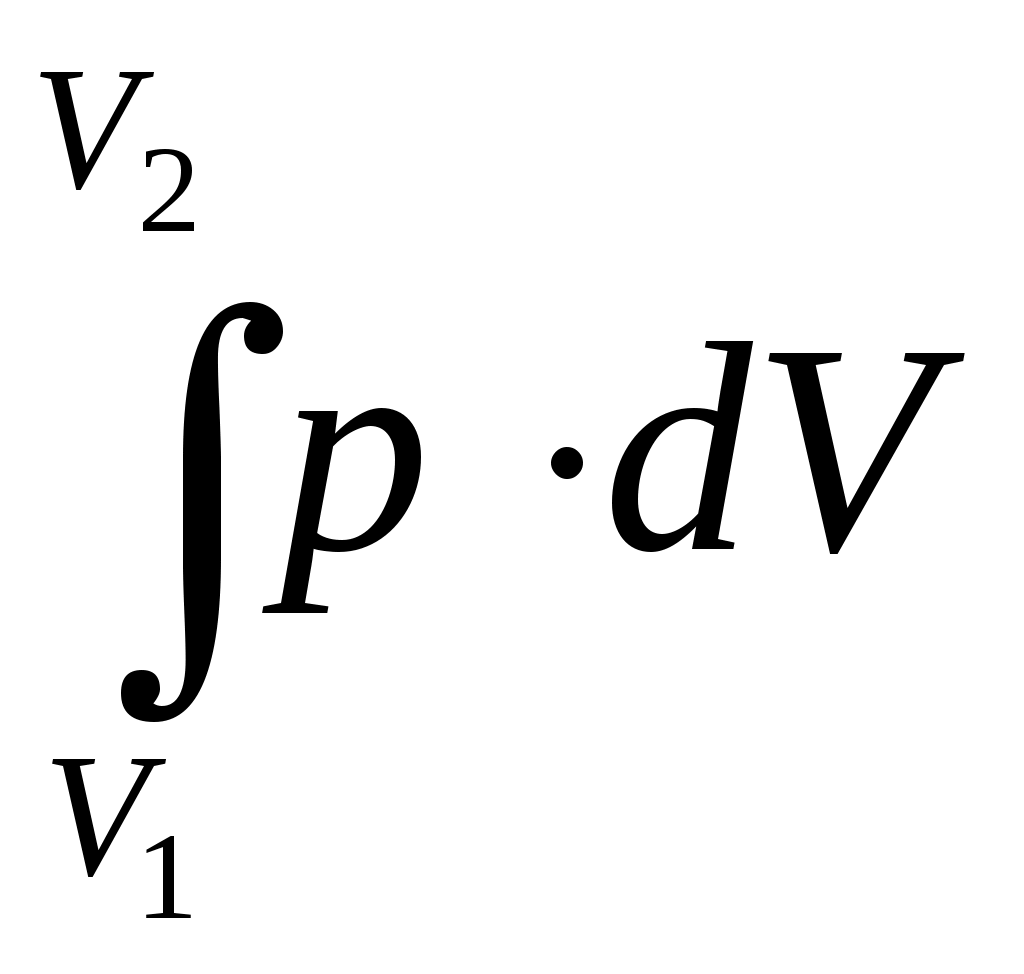 – это сумма площадей всех полосок от V1 до V2. T. о., работа газа измеряется площадью под кривой на диаграмме p–V.Очевидно, что работа зависит от процесса, т. е. от того, происходит ли расширение газа по кривой I или по кривой II (видно, что на рис. б под кривой II площадь больше, чем под кривой I).
– это сумма площадей всех полосок от V1 до V2. T. о., работа газа измеряется площадью под кривой на диаграмме p–V.Очевидно, что работа зависит от процесса, т. е. от того, происходит ли расширение газа по кривой I или по кривой II (видно, что на рис. б под кривой II площадь больше, чем под кривой I).При изобарическом процессе ( рис. а, кривая I) работа газа:
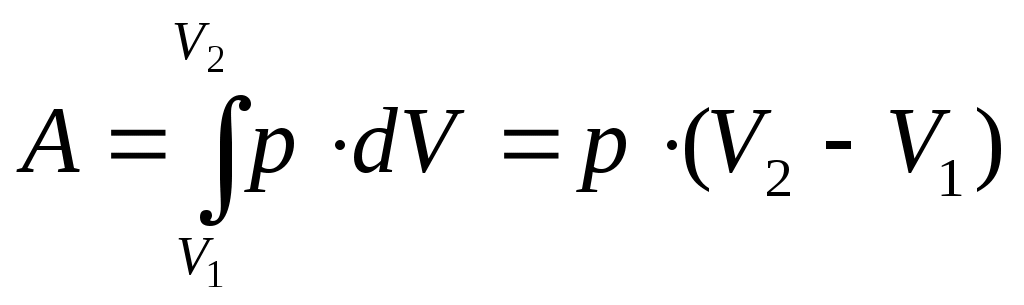 (22).
(22).При изохорическом процессе ( рис. а, кривая II) объем не меняется, т. е. dV= 0 и, следовательно, А = 0. При изотермическом процессе меняются и р, и V ( рис. б). Заменив давление через объем и температуру, согласно уравнению (4), получим работу газа при T=const :
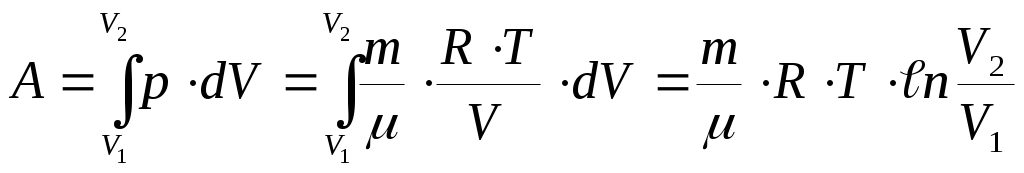 (23).
(23). Проведем процесс расширения газа из состояния 1 (рис. б) в состояние 2 по кривой II (А>0), а сжатие обратно в состояние 1 – по кривой I (А<0). Процесс с возвращением в ту же точку называется циклом. Тогда общая работа будет равна разности площадей под кривыми II и I, т. е. площади цикла.
Если цикл на диаграммах p–V совершается по часовой стрелке (см. рис. б), то работа при расширении больше, чем при сжатии и полная работа А > 0. Поскольку мы возвращаемся в ту же точку, ΔU = 0. Из (18) следует, что при таком процессе и теплота, подводимая к телу, должна быть больше нуля (Q> 0). Так происходит в тепловой машине, когда тепло подводится, а машина производит положительную работу.
Если же цикл совершается против часовой стрелки, то А < 0. Соответственно и Q < 0, т. е. энергия не подводится к телу, а отводится от него. Это имеет место в холодильнике.
В обоих случаях происходит обмен энергией с окружающей средой либо в виде работы, либо в виде обмена теплотой.
Теплоемкость. Молярная теплоемкость газа. Степени свободы.
Под теплоемкостью С телапонимают то количество тепла, которое надо сообщить телу, чтобы повысить его температуру на один градус Кельвина:
Если передается энергия не всему телу, а одному килограмму, то говорят об удельной теплоемкости с = С/m( Дж/(кг·К)). Если речь идет об одном моле, то говорят омолярной теплоемкости
Поскольку при переходе тела из одного состояния в другое δQзависит от процесса, по которому производится этот переход, теплоемкость тоже зависит от процесса. Если процесс изохорический (V = const), то теплоемкость обозначается СV. Если процесс изобарический, то – Ср. При изотермическом процессе dT = 0, a δQне равно нулю и соответствующая теплоемкость устремляется к бесконечности СТ → ∞.
Определим СV (теплоемкость 1 моля при постоянном объеме), использовав первое начало термодинамики в дифференциальной форме (19).
Поскольку V = const, тоdV = 0 и δA= 0 и для СVполучаем:
Значок вне скобок указывает на тип процесса, т. е. что V= const. Соотношение (25) означает, что при постоянном объеме все подводимое тепло идет только на изменение внутренней энергии U.
При изобарическом процессе (р = const), для теплоемкости Ср получаем:
Найдем (dV/dT)pиз уравнения Клапейрона (4):
и подставив в (26), получим уравнение Майера:
Cp больше, чем СV , так как подведенная теплота идет не только на увеличение внутренней энергии, но и на работу расширения газа.
Определим dU/dT, так как эта производная входит в (25) и (26). Для идеального газа внутренняя энергия равна сумме средних кинетических энергий всех N молекул:
 Если молекула двухатомная (рис.), то, кроме поступательного движения, она может еще вращаться вокруг осей xи y.
Если молекула двухатомная (рис.), то, кроме поступательного движения, она может еще вращаться вокруг осей xи y.Вращение вокруг оси zне дает вклада в энергию, так как энергия вращательного движения равна J·ω2/2 = m·r2·ω2/2, а двухатомная молекула не имеет пространственной протяженности вдоль осей xи y.
Надо не только задать три координаты, чтобы определить положение центра масс молекулы в пространстве, но и задать еще две (вращательные) координаты, чтобы определить ее ориентацию в пространстве. Т.о., число степеней свободы для двухатомной молекулы i = 5.
Для трех- и более атомной молекулы вклад в энергию даст и вращение вокруг оси z . Для них i= 6 .
Молекулы мы считали жесткими; колебательные степени свободы не
учитывались. Если их учесть, результат будет немного иной, но колебательные степени свободы становятся существенными только при высоких температурах.
Итак, для жестких молекул внутренняя энергия и молярные теплоемкости равны:
Все это сильно упрощенные рассуждения, непригодные, например, при очень низких или высоких температурах. Более последовательная теория теплоемкости строится на основе квантовой физики.
1 2 3 4 5 6 7 8 9 ... 19
Адиабатический процесс
Процесс без обмена теплотой с окружающей средой называется адиабатическим. Он может происходить, если газ (или другое тело) окружен абсолютно не проводящей тепло оболочкой или процесс происходит очень быстро, так что газ не успевает обменяться теплом с другими телами.
При таких процессах первое начало термодинамики упрощается:
δQ = 0; dU = – δА. (32) .
Это означает, что если над газом производить работу (δА < 0), то dU > 0. Внутренняя энергия газа возрастает, он нагревается. Если же газ расширяется, то он сам производит работу δА > 0 за счет собственной внутренней энергии и dU < 0. В результате он охлаждается.
Согласно (25): dU=ν ·CV·dT. ДляδА используем соотношение (20). Тогда выражение (32) для адиабатического процесса можно записать так:
Подставим сюда р из уравнения Клапейрона-Менделеева (4) иполучим:
Проинтегрируем последнее выражение для пределов изменения переменных от T1 до T2 и от V1 до V2 и введя обозначение
а используя Т = p·V/(ν·R) , получаем
Соотношения (36-37) носят название уравнений Пуассона или адиабаты. γ – показатель адиабаты.
П
 оскольку γ > 1, давление в (37) обратно пропорционально не
оскольку γ > 1, давление в (37) обратно пропорционально не
V, как было при изотермическом процессе, а Vγ, т. е. давление убывает с увеличением объема быстрее. На рисунке a кривые 1 и 2 – изотермы (Т2 < T1), а кривая 3 – адиабата.
При любых других процессах (неизотермических и неадиабатических) всегда можно связь между р и V написать в виде (37), но γ уже не будет равна Ср/СV .
В этих случаях процесс называется политропическим, а γ – показателем политропы.
Можно сказать, что для изотермического (T=const) процесса γ = 1, для изобарического (р = const) γ = 0, для изохорического (V = const) γ = ∞. На рисунке б показаны различные процессы расширения газа: 1 – изотерма, 2 – адиабата, 3 – изохора, 4 – изобара, 5 – политропа. Процессы 2, 3 идут с охлаждением, а 4, 5 – с нагреванием газа.
Круговые процессы (циклы). Цикл Карно
Газ, получая тепло и расширяясь, производит работу. Для непрерывного получения работы нужно, чтобы рабочее тело все время возвращалось в исходное состояние и снова повторялся тот же процесс, т. е. чтобы процесс был круговым, циклическим. При этом какую-то работу надо совершать над газом, сжимая его и возвращая в исходное состояние. Для того, чтобы тепловая машина совершала положительную работу необходимо, чтобы расширение газа происходило при более высоком давлении, чем сжатие. Это возможно, если при расширении в систему будет поступать энергия Q1 извне, например, от нагревателя, а при сжатии энергия Q2 должна быть отдана внешней среде – холодильнику.
После совершения цикла мы возвращаемся в исходное состояние с той же внутренней энергией. Следовательно, Δ
U = 0, а подведенное тепло Q1, за вычетом отдаваемого холодильнику Q2, переходит в полезную работу A=Q1 – Q2. Для оценки эффективности работы вводят коэффициент полезного действия (кпд) тепловой машины:
Работа машины тем эффективнее, чем больше можно получить от нее работы Aи чем меньше надо подводить тепла от нагревателяQ1.
Как показал С.Карно, максимальный кпд получается для цикла, состоящего из двух изотерм и двух адиабат (т.н. цикл Карно) (рис.) Газ расширяется из точки 1 в точку 2 по изотерме при температуре Т1 . При этом в уравнении (19) ΔU= 0, работа расширения газа A > 0, т.е., к газу должна подводиться энергия от нагревателя Q1 > 0.
П
 ри расширении по адиабате из точки 2 в точку 3 обмен теплотой равен нулю и работа расширения А производится за счет изменения внутренней энергии ΔU (газ охлаждается). Далее, внешние силы сжимают газ по изотерме 3 → 4 при температуре Т2. Здесь опять ΔU= 0, и из (19) следует, что А < 0, Q2 < 0. Чтобы произвести изотермическое сжатие, надо отводить тепло, отдавать его более холодному телу – холодильнику. Далее внешние силы сжимают газ по адиабате 4 → 1, возвращая газ в первоначальное состояние.
ри расширении по адиабате из точки 2 в точку 3 обмен теплотой равен нулю и работа расширения А производится за счет изменения внутренней энергии ΔU (газ охлаждается). Далее, внешние силы сжимают газ по изотерме 3 → 4 при температуре Т2. Здесь опять ΔU= 0, и из (19) следует, что А < 0, Q2 < 0. Чтобы произвести изотермическое сжатие, надо отводить тепло, отдавать его более холодному телу – холодильнику. Далее внешние силы сжимают газ по адиабате 4 → 1, возвращая газ в первоначальное состояние.Пользуясь формулами (23), (36) и (38), можно получить для рассматриваемого цикла Карно :
Из (39) следует, что кпд η тем больше, чем выше температура нагревателя Т1 и чем ниже температура холодильника Т2 .
Необратимые процессы
 Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.
Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.Другой пример: пусть газ находится и слева и справа от теплопроводной перегородки, но температура слева выше, чем температура справа (рис. б). Молекулы обмениваются с перегородкой кинетической энергией, и постепенно температуры обеих частей выравниваются. Такой процесс передачи тепла всегда необратим. Самопроизвольно средняя кинетическая энергия молекул (т. е. температура) слева сама не поднимется за счет кинетической энергии молекул справа.
Любой процесс, сопровождающийся трением, также необратим, так как при этом энергия упорядоченного движения переходит в энергию беспорядочного движения молекул, т. е. в теплоту.
Энтропия
Пусть с рабочим веществом совершаются циклы, при каждом из которых подводится от нагревателя Q1, отдается холодильнику Q2 и производится работа
А = Q1 – Q2 . Из (38) и (39) можно получить:
Величина Qi /Tiназывается приведенной теплотой. Обозначим ее ΔSi . Из (40) следует, что сумма приведенных теплот при циклическом процессе равна нулю. Это означает, что, какой бы циклический процесс мы ни совершали, если мы вернулись в исходное состояние, некоторая величина Sне меняется (ΔS = 0). Следовательно, S– функция состояния. Она получила название энтропии. Таким образом, состояние определяется не только внутренней энергией U, но и энтропией S. Если процесс не циклический и тело переходит из состояния 1 в другое состояние 2, то
Рассмотрим теплопередачу при контакте двух тел при температурах Т1 и Т2 (Т1 > Т2) в теплоизолированной системе. ТеплотаQ, передаваемая телом 1, равна теплотеQ, полученной телом 2. Однако, тело 1 отдает ее при температуре Т1 и
В тепловой машине часть теплоты, взятой от нагревателя, преобразуется в работу, а другая часть должна быть передана холодильнику. Нагреватель охлаждается, а холодильник нагревается.
С одной стороны, мы знаем, что при этом энтропия возрастает. С другой стороны, к.п.д. такой тепловой машины будет постепенно падать, так как
Энтропию можно связать со степенью упорядоченности системы. Увеличение энтропии соответствует увеличению беспорядка. Энтропия – это мера беспорядка. В наших примерах (рис.) система переходила из менее вероятного, упорядоченного, неравновесного состояния в более вероятное, неупорядоченное, равновесное.
Вычислим изменение энтропии для идеального газа, исходя из дифференциальных выражений для изменения энтропии и I начала термодинамики:
dS=δQ / T ;
Учитывая, согласно уравнению Клапейрона , что
Второе начало термодинамики
Первое начало термодинамики (19, 41), т. е. закон сохранения энергии, справедливо при любом процессе обмена энергией. Оно не указывает направление процесса, для него неважно, будет ли тепло передаваться от горячего тела к холодному или наоборот, будет ли газ самопроизвольно расширяться или сжиматься и т. д..
Однако из рассмотренного выше вытекает, что:
1. Любая система, выведенная из состояния равновесия и предоставленная самой себе, возвращается в равновесное состояние. Таковы, например, необратимые процессы переноса: вещества (диффузия), энергии (теплопроводность), импульса упорядоченного движения (внутреннее трение или вязкость).
2. Механическая работа может быть полностью превращена в теплоту, т. е. энергия упорядоченного движения может полностью перейти в энергию неупорядоченного движения. Однако, энергия неупорядоченного движения (теплота) может быть преобразована в энергию упорядоченного движения (работу) лишь частично. Невозможен процесс, единственным результатом которого было бы полное превращение теплоты в работу. Т.е., кпд тепловой машины η < 1 .
3. Предоставленная самой себе система всегда переходит из менее вероятного в более вероятное состояние. Больцман получил соотношение, связывающее изменение энтропии при необратимых процессах с термодинамическими вероятностями (числом способов реализации того или иного состояния) начального W1 и конечного W2 состояний : ΔS=k·ℓn(W2/W1) . Из этого соотношения вытекает, что процессы с уменьшением энтропии не невозможны, а настолько маловероятны, что практически никогда не реализуются.
Используя понятие энтропии, можно сформулировать еще одно равносильное утверждение: «В замкнутой, изолированной системе (системе с постоянной энергией) при любых процессах энтропия не может убывать , т.е. ΔS≥0 ».
Все эти формулировки эквивалентны. Все они указывают направление процессов в изолированной или что то же самое в предоставленной самой себе системе. Это и есть второе начало термодинамики – важнейший закон природы.
Не следует думать, что этот закон вообще запрещает передачу тепла от холодного тела к нагретому. Это возможно, но только в незамкнутой (открытой) системе. Например, это осуществляется в холодильнике. Можно также уменьшить энтропию системы, например поршнем сжать газ и снова собрать его в одной половине сосуда. Можно увеличить порядок в системе (т. е. уменьшить энтропию), но для этого необходимо вмешательство внешних сил.
ФИЗИКА. Часть 2.
2.1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
Электрический заряд
В основе разнообразия явлений природы лежат четыре фундаментальных взаимодействия между элементарными частицами – сильное, электромагнитное, слабое и гравитационное. Каждое взаимодействие связывается с определенной характеристикой частицы. Например, гравитационное взаимодействие зависит от масс частиц, электромагнитное – от электрических зарядов и т. д.
Электрический заряд частицы является одной из основных, первичных ее характеристик. Ему присущи следующие фундаментальные свойства:
– дискретность: существует минимальный заряд, равный 1,6.10-19Кл; – двузначность: существуют положительные и отрицательные заряды; – инвариантность относительно преобразований Лоренца: величина заряда остаётся неизменной независимо от того, движется он или покоится; – сохранение заряда в изолированной системе: полный заряд электрически изолированной системы остаётся постоянным.
Заряд называется точечным, если можно пренебречь размерами заряженного тела по сравнению с расстоянием от этого тела до других зарядов. Любое заряженное тело можно рассматривать как совокупность точечных зарядов.
1 2 3 4 5 6 7 8 9 ... 19