Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc

Дифракция света.

Принцип Гюйгенса-Френеля. Зоны Френеля.

Дифракция – явление отклонения света от прямолинейного распространения в неоднородной среде, при котором свет, огибая препятствия, заходит в область геометрической тени, – возни­кает, когда свет падает на препятствия, размеры которых сравнимы с длиной световой волны.

По принципу Гюйгенса, каждую точку фрон­та волны можно рассматривать как самостоя­тельный источник вторичных сферических волн. По Френелю, волновое возмущение в любой точке пространства – результат интерферен­ции этих вторичных когерентных волн. Различают т.н. дифракцию Френеля или сферических волн и дифракцию Фраунгофера или плоских волн.

Метод зон Френеля. Волновую поверхность разбивают на зоны так, чтобы расстояния от краев соседних зон до точки наблюдения Pотличались на λ/2 (рис.).

В этом случае фазы приходящих от соседних зон колеба­ний отличаются на π , сами колебания противоположны по фазе, поэтому при наложении волн они взаимно ослабляют друг друга. Тогда амплиту­да Eрезультирующих колебаний может быть представлена в виде знакопеременного ряда:



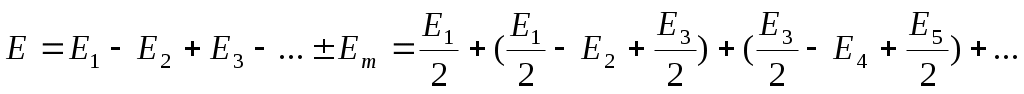
Дифракция Френеля на круглом отверстии. Пусть в отверстии помещается m зон. Так как амплитуды сферических волн убывают с увеличением расстояния до т.Р, то приближенно выполняется равенство: E_k=(E_k-1+E_k+1)/2 , т.е. амплитуда волны от k-зоны равна среднему арифметическому амплитуд волн от примыкающих к ней зон. Тогда все выражения в круглых скобках обращаются в нуль и для результирующей амплитуды колебаний в т.Р получим: 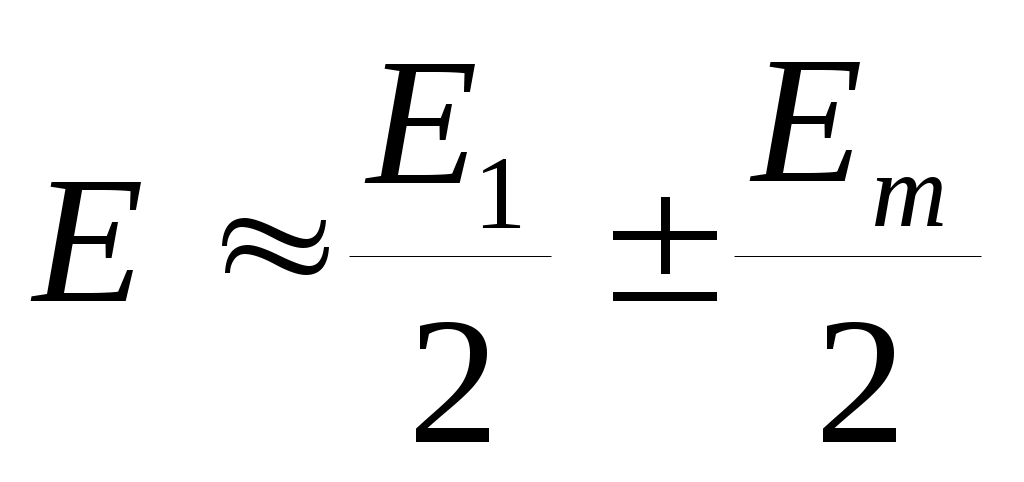, где: знак «+» соответствует нечетному числу m зон , открываемых отверстием (например, для m = 5 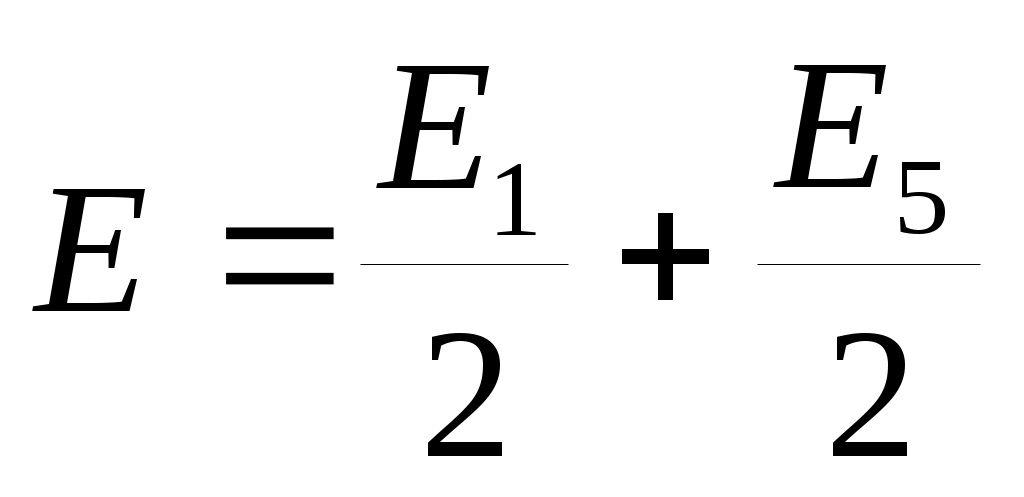и наблюдается максимум – светлое пятно); знак «–» соответствует четному числу m зон , открываемых отверстием (например, для m = 4 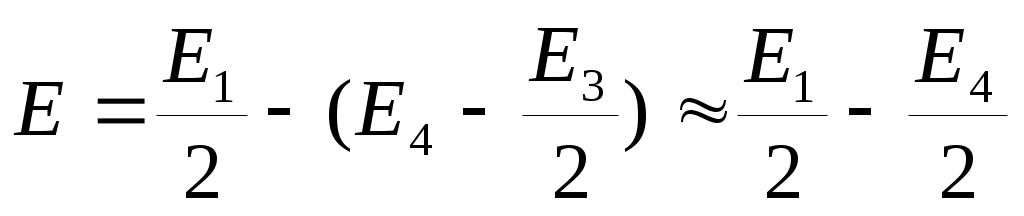и наблюдается минимум – темное пятно). Если отверстие будет большим (или экрана вообще не будет), то поместятся много зон и в результате 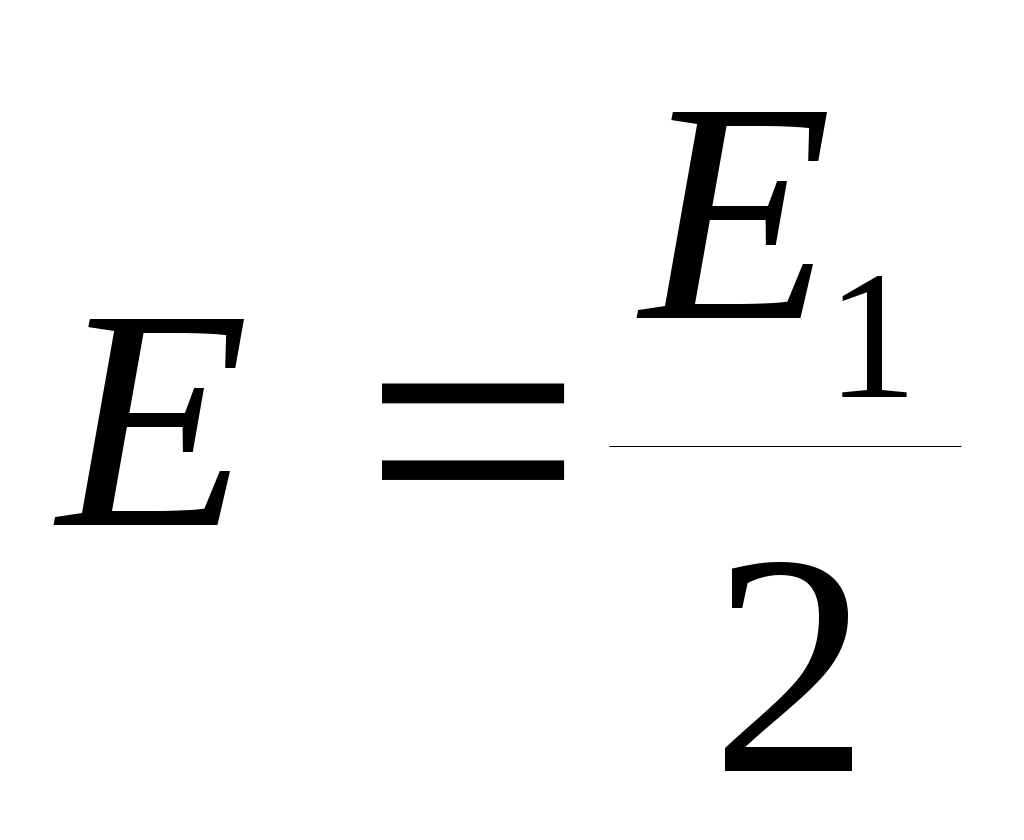. Это означает, что в т.Р попадает свет только от первой зоны, и таким образом объясняется прямолинейное распространение света.

Е сли на место Рпоместить экран, то вокруг точки Р будут минимумы и макси­мумы освещенности, имеющие форму колец.. В центре, т. е. в точке Р, может быть как свет, так и темнота, в зависимости от числа зон Френеля, уместившихся в отверстии. Эти теоретические рас­суждения прекрасно подтвердились на опыте.

Но самый поразительный результат был получен при рассмот­рении дифракции на круглом непрозрачном экране(рис.). В этом случае несколько центральных зон (например, m) закрыва­ются, а все остальные зоны открыты. Это значит, что в центре тени от малого предмета всегда должно быть свет­лое пятнышко (рис.) 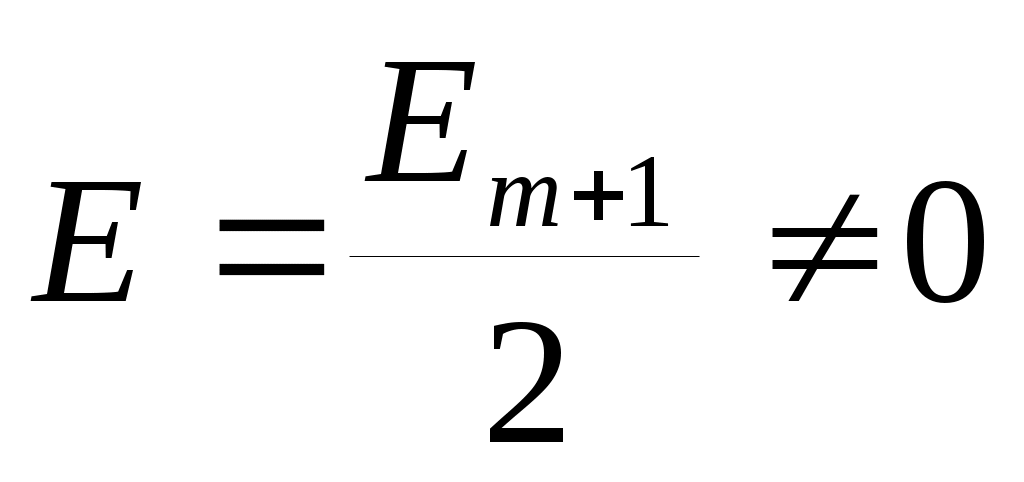. Оно получило название пятна Пу­ассона. На опыте это подтвердилось, что стало блестящим доказательством волновой природы света.

Дифракция Фраунгофера на щели

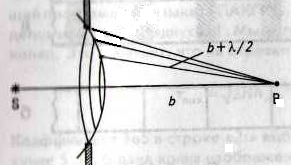
П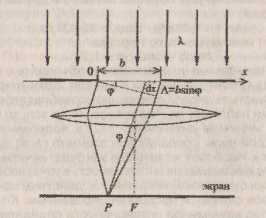 лоская электромагнитная волна падает нор­мально на преграду со щелью ширины b.

Если бы не было дифракции, световые лучи, пройдя через щель, сфокусировались бы в точ­ке F, лежащей на главной оптической оси линзы (рис.). Однако, наблюдаемое на экране распределение интенсивности света имеет в центре резкий максимум освещенности, относительно которого симметрично располагаются чередуясь светлые и темные полосы.

Наблюдаемую дифракционную картину можно объяснить с по­мощью построения зон Френеля. Разобьем открытую часть волновой поверх­ности на N элементарных зон ширины b/N. Каж­дая зона создает вторичные волны одинаковой амплитуды E₀ / N.

Если откры­тая часть волновой поверхности разбивается из точки наблюдения Р на четное число зон, то бу­дет минимум интенсивности, т.к. колебания от каждой пары соседних зон приходят в противофазе и взаимно гасят друг друга. Наоборот, если число зон будет нечетным, то результирующая интенсивность в точке наблю­дения будет максимальной, т.к. действие одной из зон окажется нескомпенсированным.

Т.о., условие дифракционного минимума: b·sinφ=m·λ.

Условие дифракционного максимума: b·sinφ=(2·m+1)λ/2.

Дифракция Фраунгофера на дифракционной решетке

Дифракционная решетка – это система из большого числа N параллель­ных друг другу щелей шириной b. Щели разделе­ны непрозрачными, равными по ширине, про­межутками а. Расстояние d = а + bназывается периодом решетки.

Пусть плоская монохроматическая световая волна интенсивности I₀ падает на решетку нор­мально. Колебания, исходящие от щелей, коге­рентны, они интерферируют друг с другом, и дифракционная картина состоит из достаточно узких интенсивных максимумов.

В центр дифракционной картины (φ = 0) коге­рентные колебания от всех щелей приходят в фазе, поэтому наблюдается центральный максимум освещенности.Аналогичный резуль­тат получается и при углах дифракции φ, для кото­рых оптическая разность хода Δ колебаний от со­седних щелей равна целому числу длин волн:

Δ=d·sinφ=m·λ. (m=0,1,2…)

В направлениях φ, определяемых этим уравне­нием, возникают максимумы. Их называют глав­ными максимумами m-го порядка, а само урав­нение – у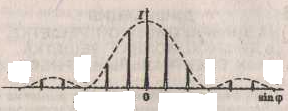 словием главных максимумов (рис. ).

Из этой формулы следует, что лучи различной длины волны будут иметь максимумы в различ­ных направлениях. Если на дифракционную ре­шетку падает белый свет, то центральный мак­симум (φ = 0) будет представлять собой белую полосу. Во всех остальных порядках будет наблюдаться радужное цветовое размытие (сплошной спектр), обращенное к централь­ной белой полосе фиолетовым краем.

С увеличением числа щелей растут интенсив­ность и резкость главных максимумов.

Положение минимумов освещенности для дифракционной решетки определяется также, как и для одной щели: b·sinφ= m'·λ., где m' = 1,2,3...

Разрешающая способность решетки по­казывает ее способность различать две очень близко расположенные линии в спектре и определяется формулой R=λ/Δλ,

где Δλ – наименьшая разность длин волн двух соседних спектральных линий λ и λ+Δλ, при которой эти линии в спектре видны раздельно.

Угловая дисперсия D определяет угловую ширину спектра D = dφ/dλ. Она численно равна угловому расстоянию dφ между двумя линиями спектра, длины волн которых различаются на единицу.

Дифракция рентгеновских лучей. Для рентгеновских лучей в качестве дифракционной решетки можно использовать кристаллы, в которых расстояние между атомными плоскостями d сравнимо с длиной волны λ

(λ

10

---

^-9м). При рассмотрении дифракции рентгеновских волн, отразившихся от соседних атомных слоев, удобно использовать угол скольжения θ к поверхности кристалла, а не угол падения. Из рис. можно найти оптическую разность хода: Δ = 2dsinθ. Условие максимума будет

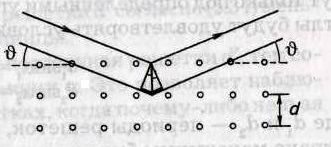2dsinθ= mλ, (m=1,2,3,…).

Это соотношение известно как формула Вульфа–Брэгга. С помощью рентгеноструктурного анализа можно изучать структуру кристаллов, определять межатомные расстояния. В частности, так была расшифрована структура молекулы ДНК – т.н. двойной спирали.
3.2. ПОЛЯРИЗАЦИЯ И ДИСПЕРСИЯ СВЕТА.

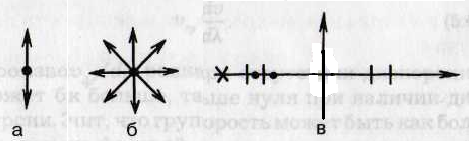Поляризация света. Электромагнитная волна – поперечна, колеблющиеся в ней векторы и перпендикулярны друг другу и направлению рас­пространения. При взаимодействии со средой основную роль играет вектор , так как электрическое поле действует на электроны и поляризует среду. На рис. а показан луч света, идущий на нас, и вектор . Этот вектор колеблется и на рис. направ­лен то вверх, то вниз, все время меняясь по величине. Плоскость, в которой он колеблется, называется плоскостью поляризации. Такой свет называется поляризованным.

Однако чаще всего волны испускаются разными атомами, каждый дает свою плоскость поляризации (рис. б). Такой свет называется неполяризованным, или естественным.

Устройство, позволяющее получать поляри­зованный свет из естественного, называется поляризатором.

---

Результат действия поляризатора показан на рис. в. На этом рис. векторы в естественном свете заменены только двумя черточ­ками – вертикальной и черточкой, идущей от нас за бумагу, т. е. точкой. Дело в том, что любые косо расположенные векторы ес­тественного света всегда можно разложить на такие два направ­ления (см. рис. б). В качестве поляризатора можно использовать только систему, которая обладает свойством анизотропии. Такой системой может служить кристалл, атомы которого располагаются в виде простран­ственной решетки так, что физические свойства кристалла по разным направлениям различны. Примером может служить естественный кристалл турмалина. В 1934 г. американский ученый Э. Ланд создал пластическое вещество, способное поляризовать свет. Оно получило фирменное название "поляроид". Поляризатор пропускает только проекцию вектора на некоторую плоскость, которая на­зывается главной плоскостью поляризатора. Из поляризатора выходит поляризованный свет, интенсивность I₀ которого равна половине ин­тенсивности естественного света: I₀ = (1/2)·I_ЕСТ . При вращении поляризатора относительно луча бу­дет вращаться плоскость поляризации вышедше­го плоскополяризованного света, но его интен­сивность будет оставаться равной (1/2)·I_ЕСТ .

Если плоскополяризованный свет, интенсив­ность которого I₀, вторично пропустить через анизотропный кристалл (анализатор), то в за­висимости от ориентации анализатора из этого, поляризованного, света пропустится большая или меньшая часть.

Так как электрический вектор волны, прошед­шей первый кристалл, имеет направление, па­раллельное оси первого кристалла, то амплиту­да света, пропущенного вторым кристаллом, будет пропорциональна cosα (α – угол между осями обоих кристаллов), а интенсивность про­

---

порциональна cos²α: I=I₀·cos²α .

Это выражение называется законом Малюса. Закон Малюса позволяет определить, явля­ется ли данное излучение поляризованным. Если при пропускании света через анализатор интенсивность вышедшего света не изменяет­ся при повороте анализатора вокруг падающе­го луча, то свет – естественный, если изменяется, то – поляризованный.

Если под влиянием внешних воздействий на свет или внутренних особенностей источника света появляется предпочтительное наиболее вероятное направление колебаний, то такой свет называется частично поляризованным. Его принято характеризовать степенью поляризации , где I_MAXи I_MIN – интенсивности, соответствующие направлениям колебаний с максимальной и минимальной амплитудами, соответственно. Для естественного, неполяризованного света I_MAX= I_MIN и Р=0 . Для линейно (плоско) поляризованного света I_MIN = 0 и Р=1.

Поляризация света наблюдается при отражении и преломлении света на границе двух изотропных диэлектриков, если угол падения отличен от нуля. В отраженном луче преоблада­ют колебания, перпендикулярные к плоскости падения, в преломленном луче – колебания, параллельные плоскости падения. Степень по­ляризации зависит от угла падения лучей и по­казателя преломления отражающей среды. При определенном значении угла падения α_Б отра­женный свет полностью поляризован; прелом­ленный луч всегда поляризован лишь частично (рис.).

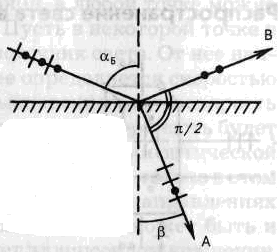
Согласно закону, установленному Брюстером, отраженный луч пол

---

ностью поляризован, если tgα_Б=n₂₁=n₂/n₁. ( n₁ и n₂ – показатели преломления сред 1 и 2, соответственно). При этом отраженный луч со­держит только колебания, перпендикулярные к плоскости падения.

Из законов отражения и преломления следу­ет, что если луч падает на диэлектрик под углом Брюстера α_Б, называемым углом полной поля­ризации, то отраженный и преломленный лучи взаимно перпендикулярны. При дальнейшем увеличении угла падения доля поляризованно­го света вновь уменьшается. Полную поляризацию при отражении под углом Брюстера можно наблюдать, если через поляризатор смотреть на блики света на диэлектрической поверхности стола и при этом вращать поляризатор. При определенном положении поляризатора бли­ки будут погашены. Это явление используется в морских бинок­лях, когда нужно убрать блики от сверкающей поверхности моря.

---