Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc

Электромагнитная индукция. Правило Ленца
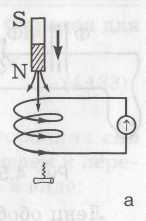Опыт показывает, что если в катуш­ку, соединенную с гальванометром, вдви­гать постоянный магнит (рис. а), то гальванометр покажет ток тогда, когда магнит движется. Если магнит, наоборот, удалять из ка­тушки, то в ней идет ток обратного направления.

Это явление, открытое Фарадеем, называет­ся электромагнитной индукцией, возникающий ток называется индукционным током, а распре­деленная по катушке э.д.с., под действием кото­рой течет ток, называется э.д.с. индукции. Причем э.д.с. индукции возникает в контуре всегда, а ток – только, если контур замкнут и яв­ляется проводником.

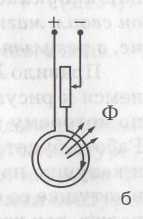Существенно именно не движение магнита, а изменение магнитного потокаФ через катушку. Например, в опыте, изображенном на верхнем рис., во внутреннем контуре возникает индукционный ток, если во внешнем с помощью реостата менять силу тока, получае­мого от внешнего источника. Причем, если во внешнем кон­туре ток увеличивать, так что поток Ф, создаваемый этим током, растет, то во

внутреннем контуре возникает индукционный ток противоположного

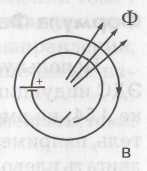направления. Он своим магнитным потоком Ф_i будет препятствовать нарастанию потока Ф. Если же силу тока в одном из конту­ров и, следовательно, поток Ф, уменьшать, например, разомкнув цепь внутреннего контура на нижнем рис., то в другом контуре возникнет индукционный ток и маг­нитный поток Ф_i того же направления, чтобы препятствовать уменьшению потока Ф.

Ленц сформулировал это следующим образом (правило Лен­ца): индукционный ток возникает такого направления, что он своим магнитным действием препятствует той причи­не, в результате которой он возник.
Формула Фарадея для э.д.с. индукции
И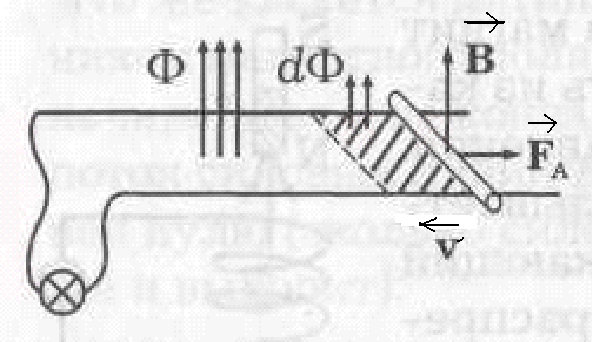
спользуя закон сохранения энергии, получим формулу для э.д.с. индукции. Рассмотрим схему на рис. Перемычку будем сами двигать влево. При этом поток Ф, пронизывающий кон­тур, будет уменьшаться на dΦ. Возникает индукционный ток Iтакого направления, что действующая на него сила Ампера F_A согласно правилу Ленца препятствует движению.

Будет совершена работа по передвижению провода с током в магнитном поле: dA = –I·dΦ. Знак «–» поставлен потому, что работу совершают сторонние силы, а не силы поля. Эта работа приводит к возникновению э.д.с. индукции ε_инд, индукционного тока и к выделению тепловой энергии в цепи: dA = I· ε_инд·dt. Приравнивая выражения для работ, получим формулу Фарадея для э.д.с. индукции: ε_инд=–dΦ/dt . Эта э.д.с. является результатом действия сторонних сил и может быть записана в виде: .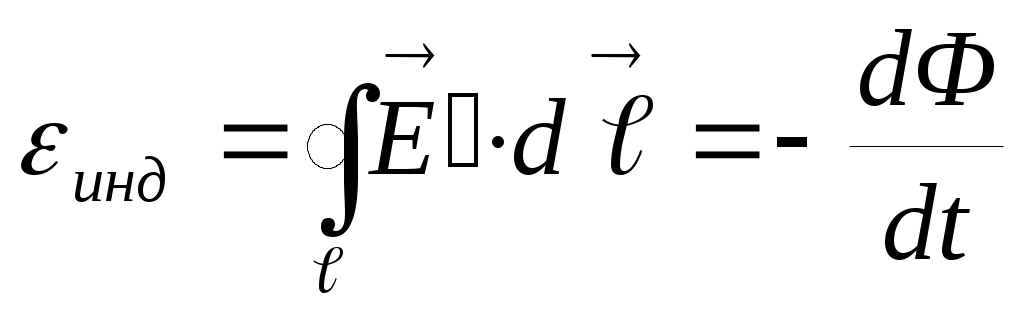

В это выражение не входят величи­ны, отражающие какие-либо свойства материа­ла, из которого сделан контур. Следовательно, э.д.с. электромагнитной индукции от этих свойств не зависит. Это позволяет считать, что измене­ние магнитного поля вызывает появление элект­рического поля. Ток, протекающий в контуре, является следствием электрического поля.

Если контур состоит из N витков, то индуцируе­мая в контуре э.д.с. будет равна сумме э.д.с. , инду­цируемых в каждом из витков в отдельности:

.

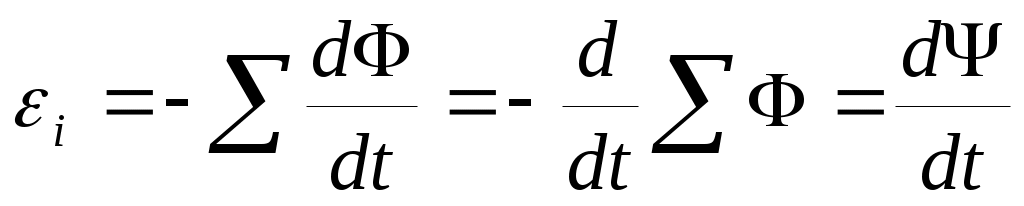Величина 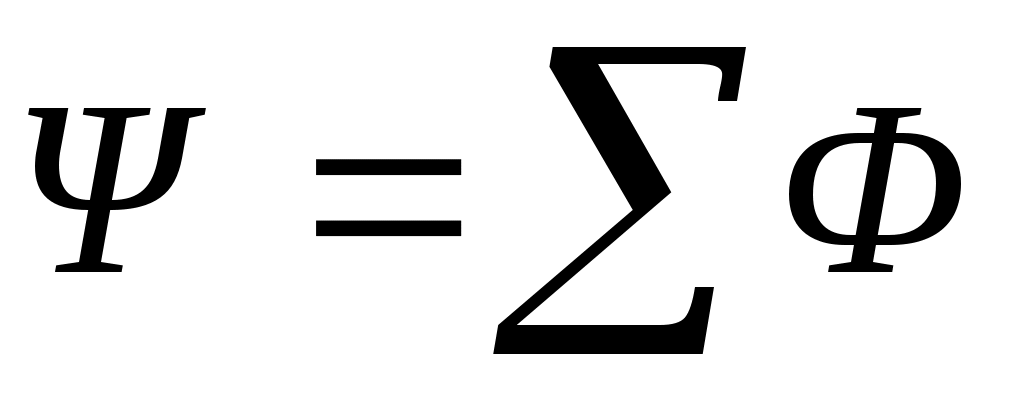называется потокосцеплением, или полным магнитным потоком. Если по­ток, пронизывающий каждый из витков, одина­ков, то Ψ=N·Φ.

Приведем выражения для э.д.с. индукции при различных способах ее возбуждения:

− э.д.с. индукции, возникающая в проводнике длиной ℓ, движу­щемся под углом α к силовым линиям со скоростью υ: ;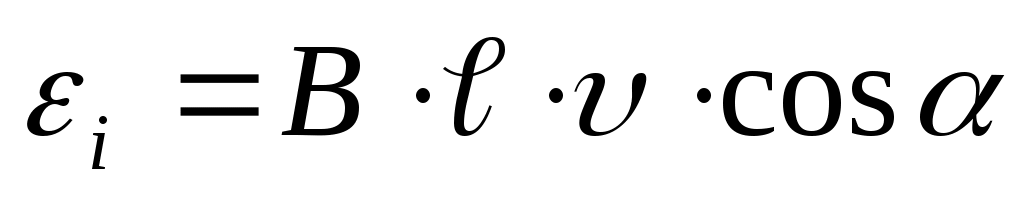

− э.д.с. индукции, возникающая в контуре , вращающемся в магнитном поле:

;

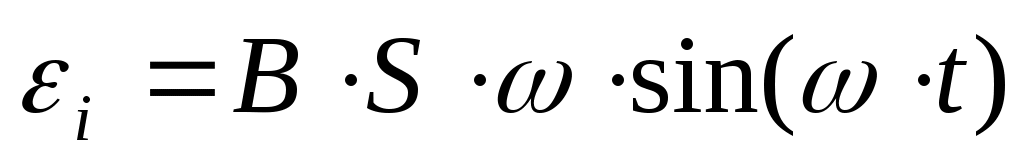− э.д.с. индукции, возникающая в контуре при изменении его площади:

;

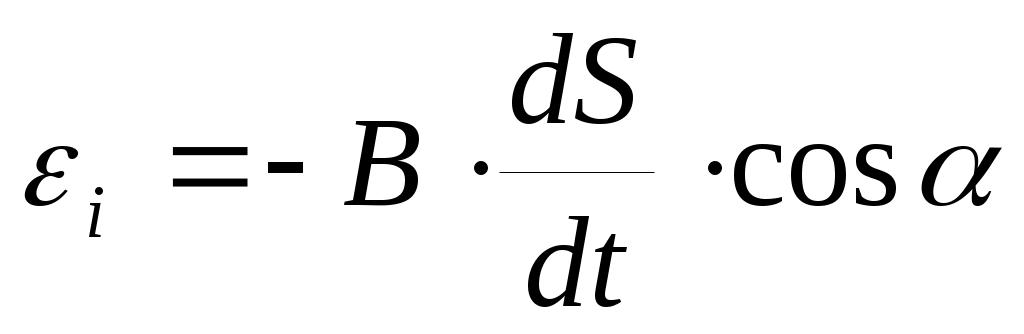− э.д.с. индукции, возникающая в контуре, помещенном в изменяющееся магнитное поле: .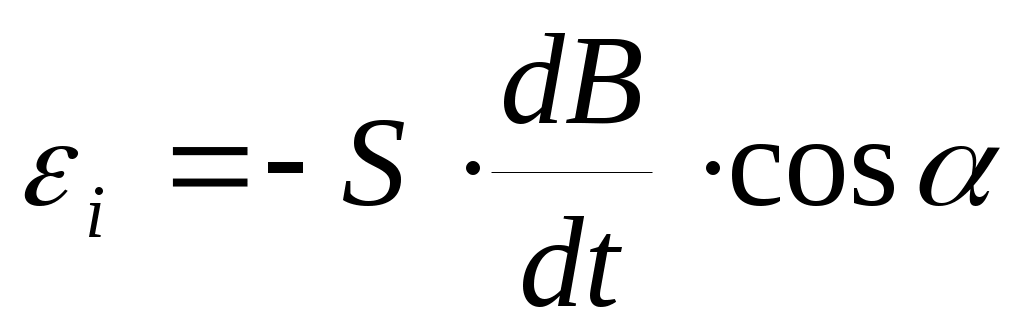
Самоиндукция

Э.д.с. индукции может возникать и в самом контуре с меняющимся токомI. Другого контура при этом может и не быть. При усилении тока (и следовательно, увеличении потока Ф) в контуре воз­никает э.д.с. индукции и индукционный ток I_инд такого направления, чтобы препятствовать усилению тока I. Это явление носит на­звание самоиндукции. Так как магнитный поток Ф, пронизывающий контур, пропорционален силе тока: Ф = L·I , то э.д.с. самоиндукции 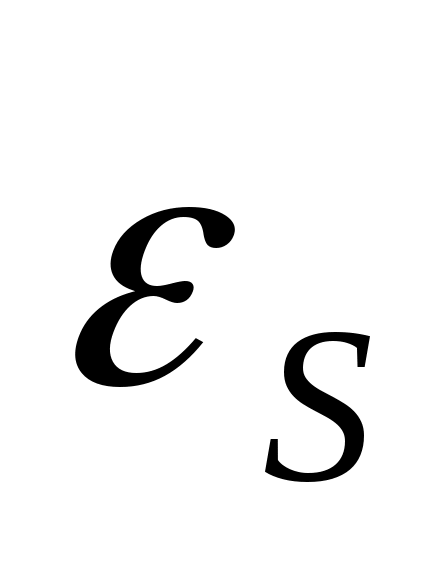пропорциональна скорости изменения тока: 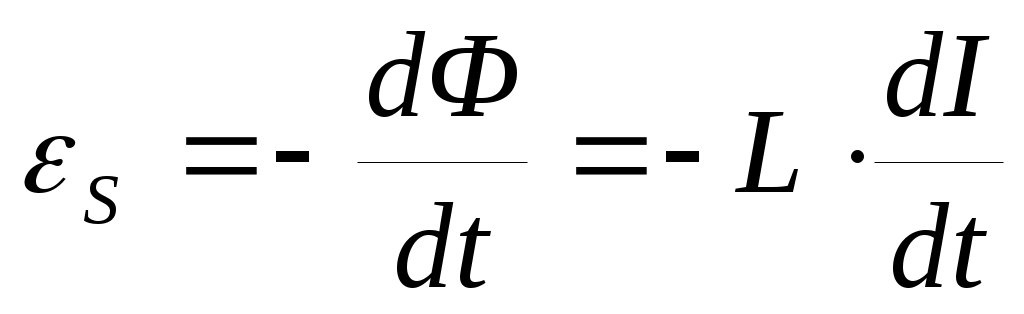, где L – коэффициент самоиндукции или индуктивностька­тушки.

Найдем индуктивность длинного со­леноида. Поток Ф через один виток равен B·S. Через все N витков соленоида Ψ = N·B·S. Индукция в соленоиде равна B=μ₀·(N/ℓ)·I. Так что

.

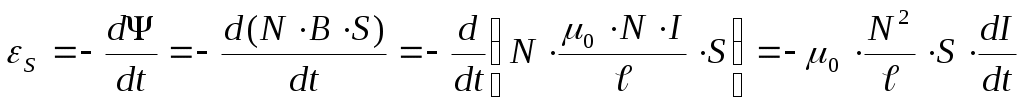Сравнивая два выражения, найдем: 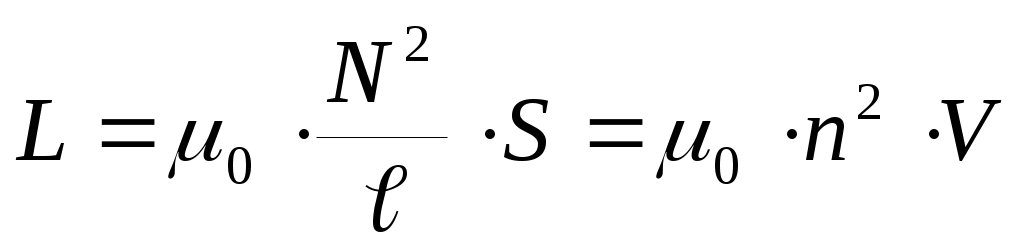, где V=S·ℓ–объем внутри соленоида, ℓ– длина соленоида, n–число витков на единице длины соленоида (густота намотки). Т.о., индуктивность соленоида очень сильно зависит от густоты намотки n.

5. 
   МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
   

Магнетики. Напряженность магнитного поля.

Все вещества являются магнетиками, т.е. при помещении их во внешнее магнит­ное поле 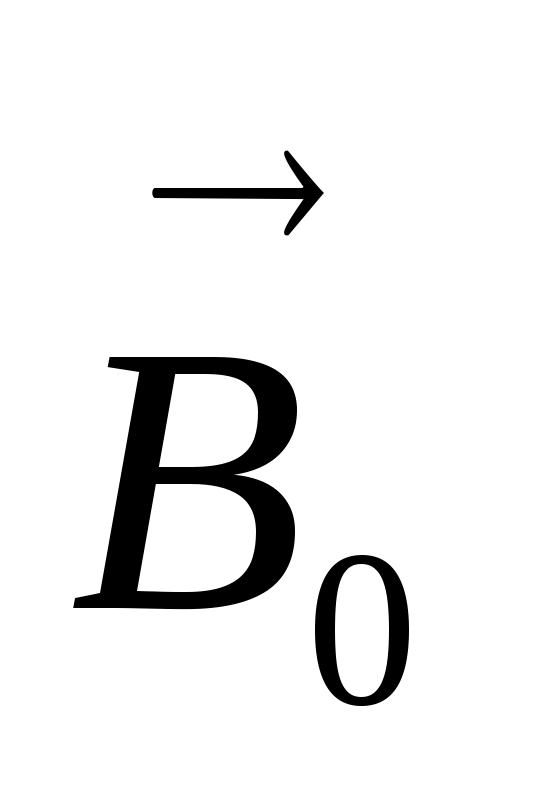изменяют свое состояние – намаг­ничиваются. Находясь во внешнем магнитном поле, намагниченные вещества сами становят­ся источниками поля 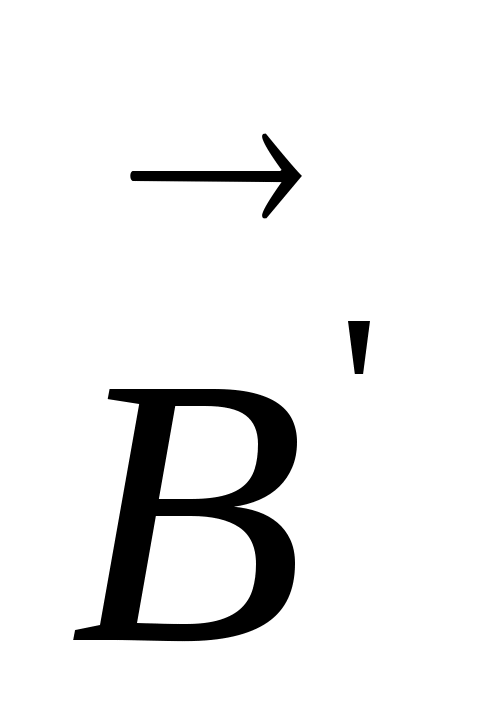. Собственное магнитное поле 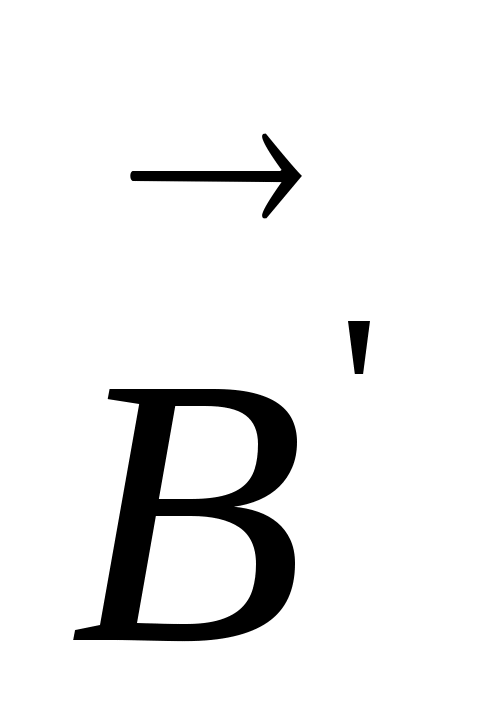, накладываясь на магнитное поле 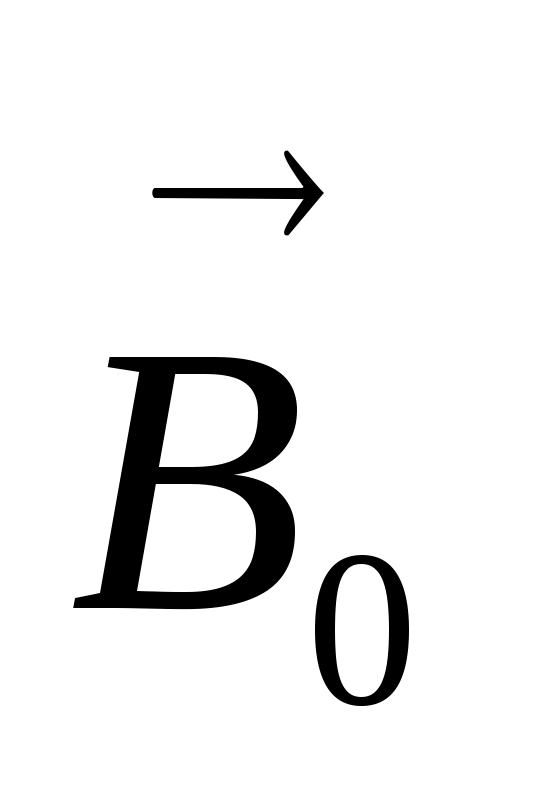, в сумме дает .

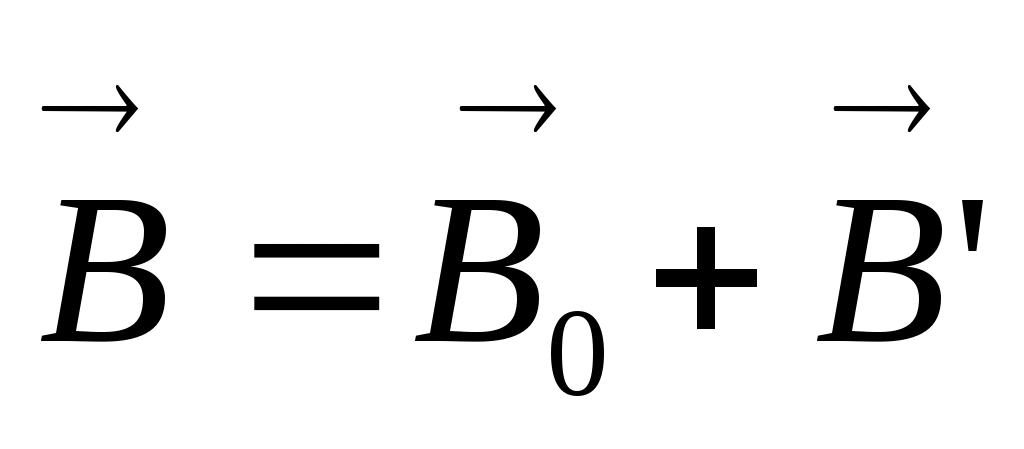Вещества, в которых поля 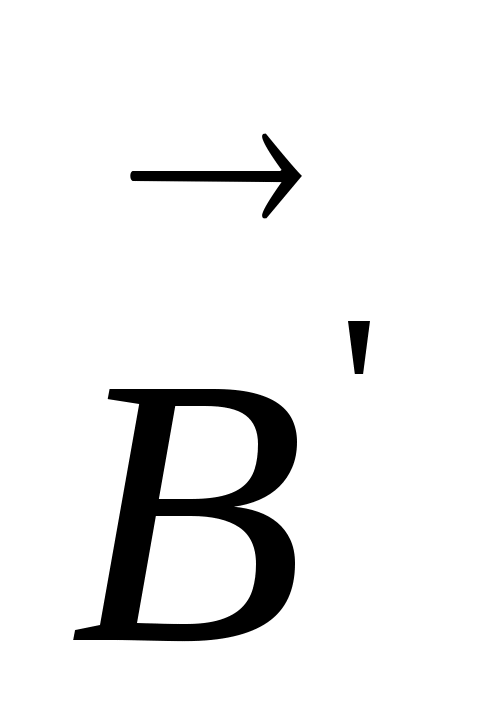и 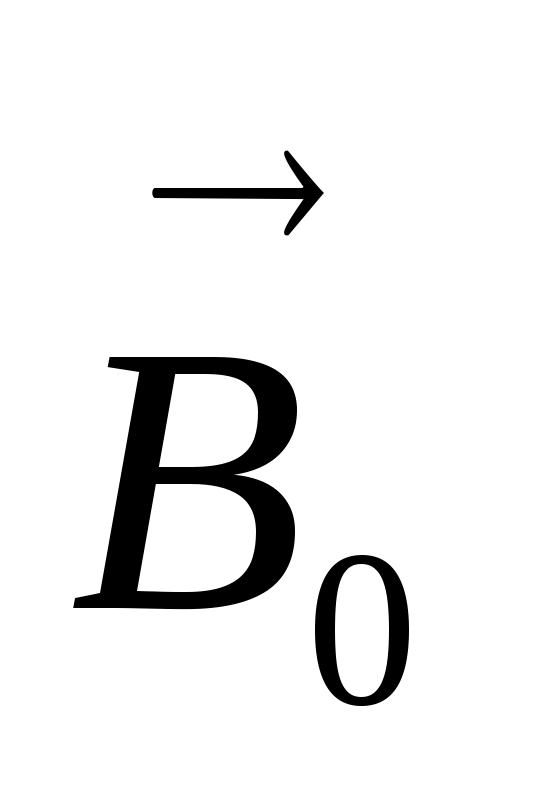направлены одинаково, называют парамагнетиками. Ве­щества, в которых поля 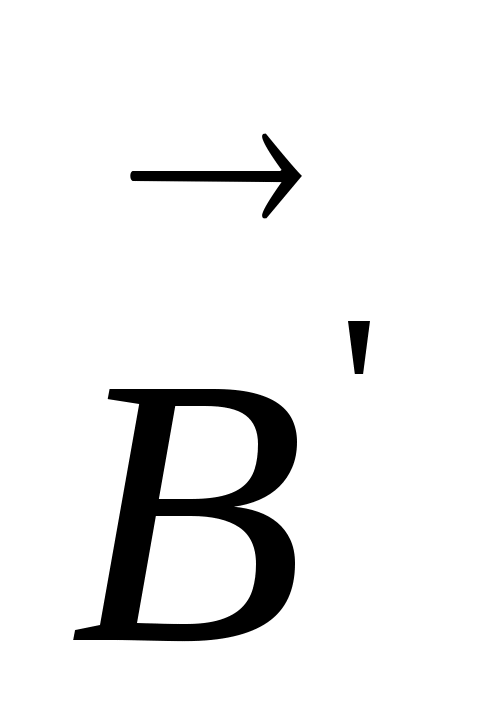и 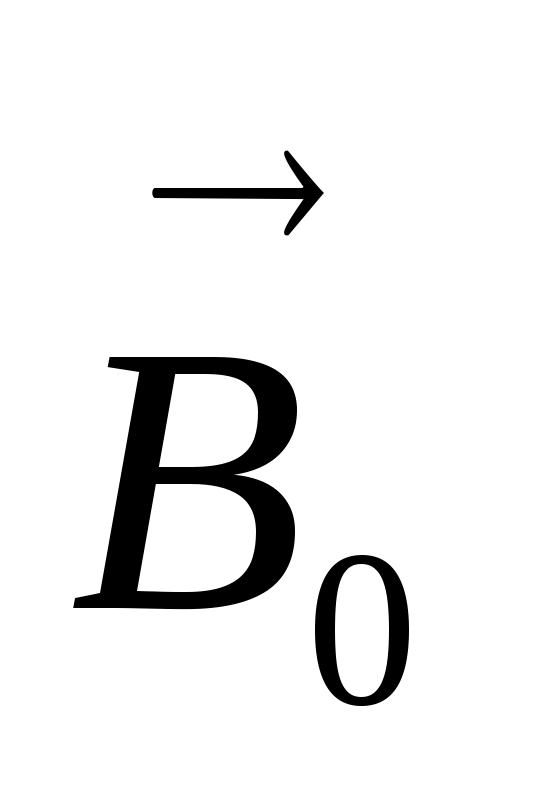направлены в противоположные стороны, называют диамагнетиками.

Степень намагничивания вещества характе­ризуется вектором намагниченности 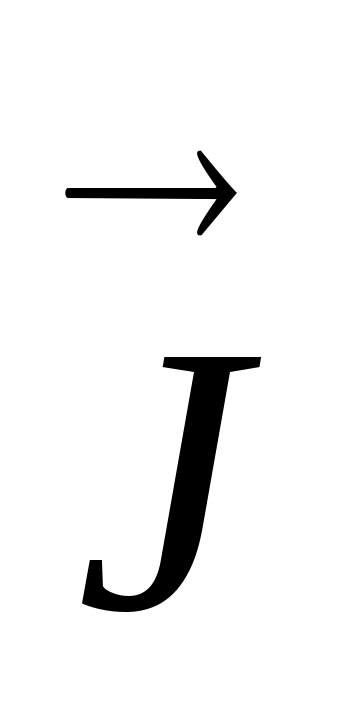. Это вектор, среднее значение которого равно отно­шению суммарного магнитного момента всех частиц, расположенных в объеме магнетика, к этому объему: 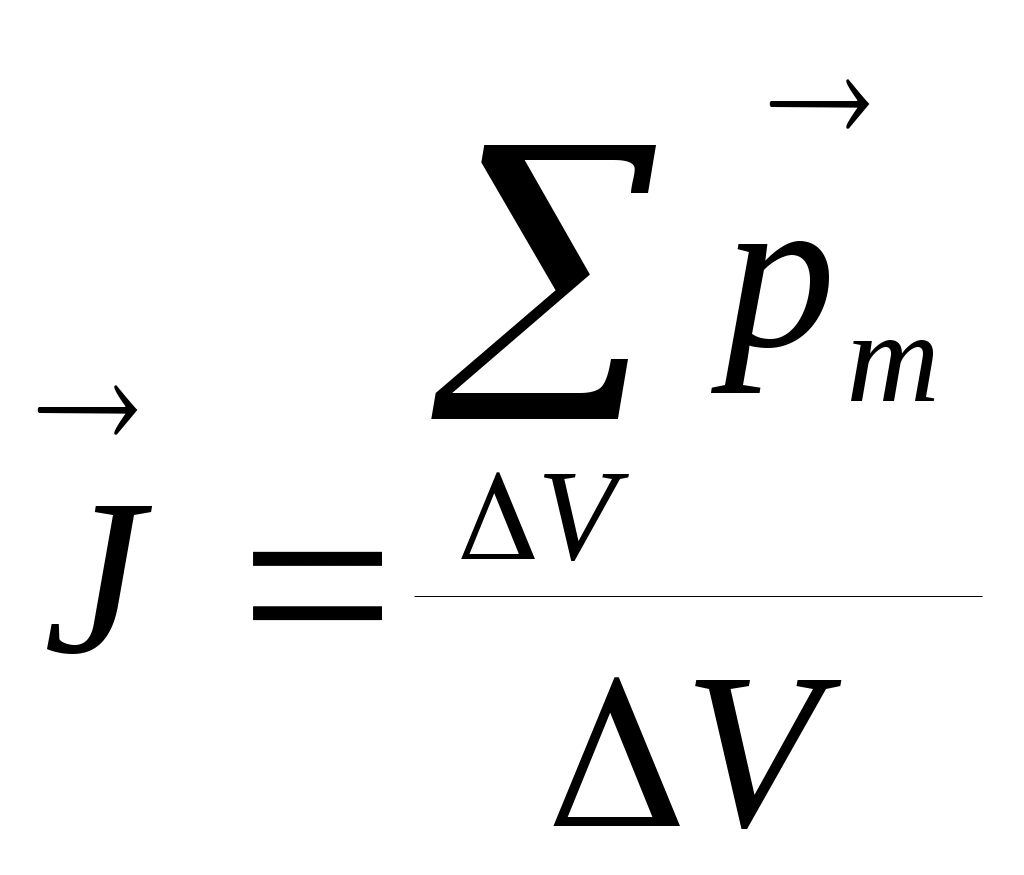, где ΔV– физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, 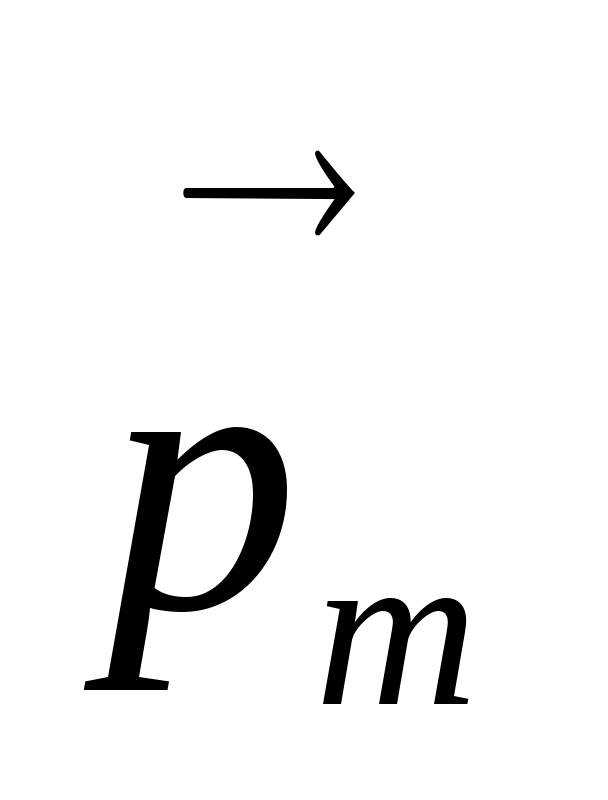– магнитный момент отдельной мо­лекулы. Суммирование производится по всем молекулам, заключенным в объеме ΔV. Единицей намагниченности является ампер на метр(А/м). Линии вектора и при наличии вещества остаются всюду замкнутыми.

Для описания поля 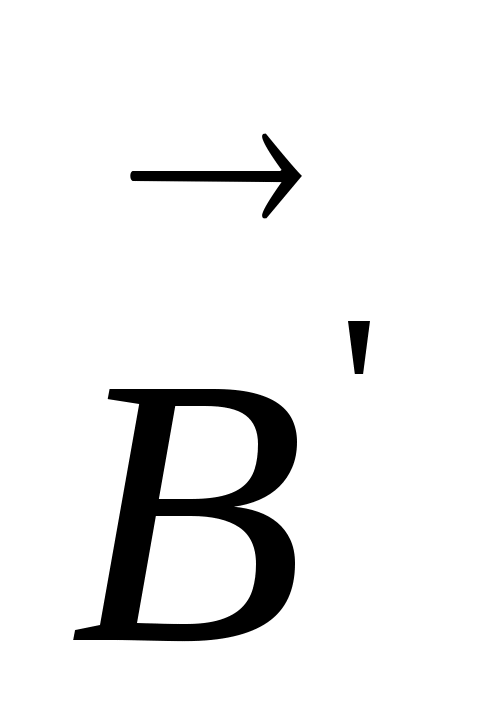, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины ℓ, внесенного в однородное внешнее магнитное поле с индукцией .

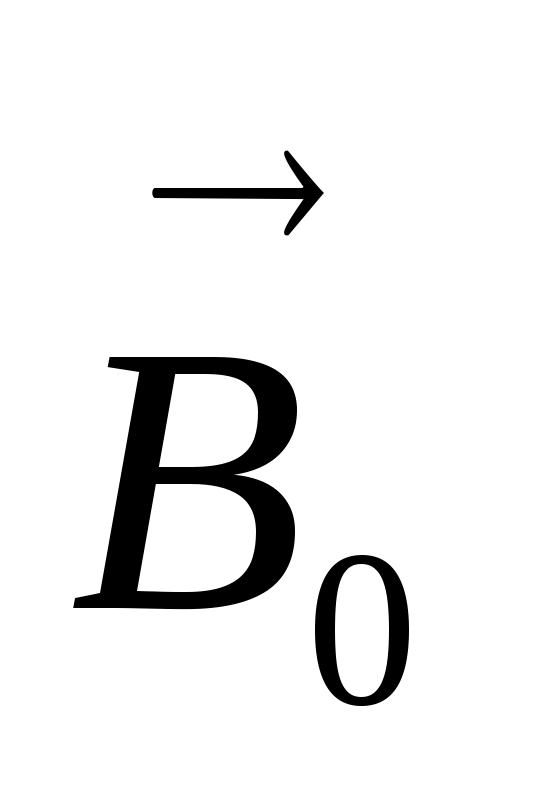В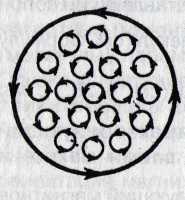 озникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору 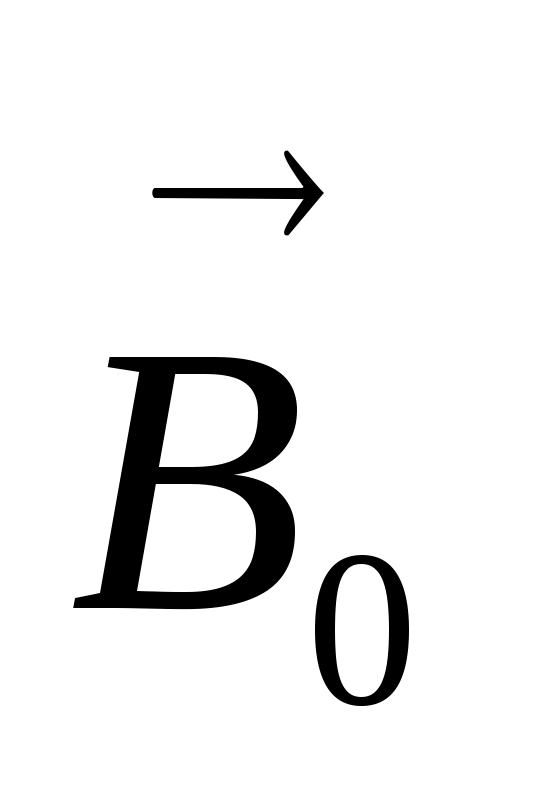. Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис.). Некомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.

Ток, текущий по боковой поверхности цилиндра I’, подобен току в соленоиде и создает внутри него поле, магнитную

индукцию В’ которого можно вычислить, учитывая

формулу для соленоида из одного витка: B’=μ₀·I’/ℓ,

где I’–сила молекулярных токов (т.н. ток намагничи-вания), ℓ – длина рассматриваемого цилиндра.

Магнитный момент этого тока P = I’·S= I’·S·ℓ/ℓ = I’·V /ℓ, где S и V — площадь сеченияи объем магнетика, соответственно. Если Р – суммарный магнитный момент магнетика объемом V, то намагниченность магнетика: J=P/V=I’/ℓ. Т.о., получим связь между B’ и J: .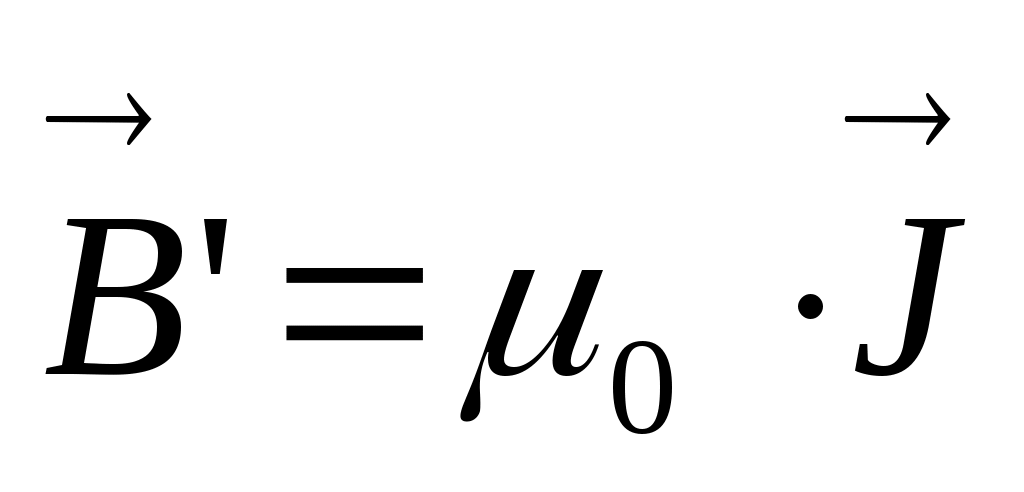

Теорему о циркуляции вектора для вещества можно представить в виде:

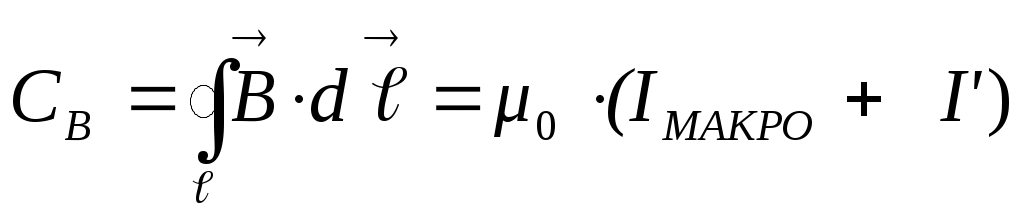. Если в этом выражении сделать замену: I’= J·ℓ , то получим 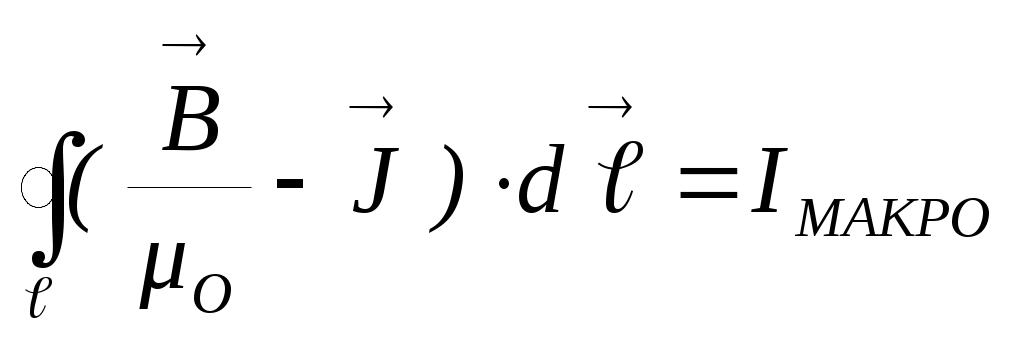или, вводя вспомогательный вектор 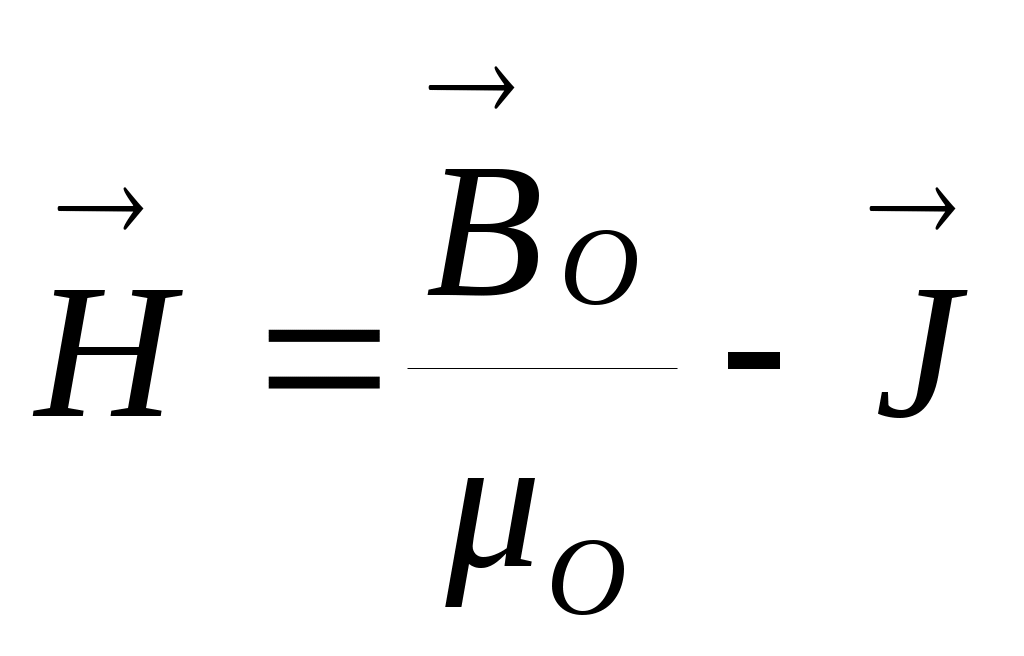, получивший название напряженности магнитного поля,: 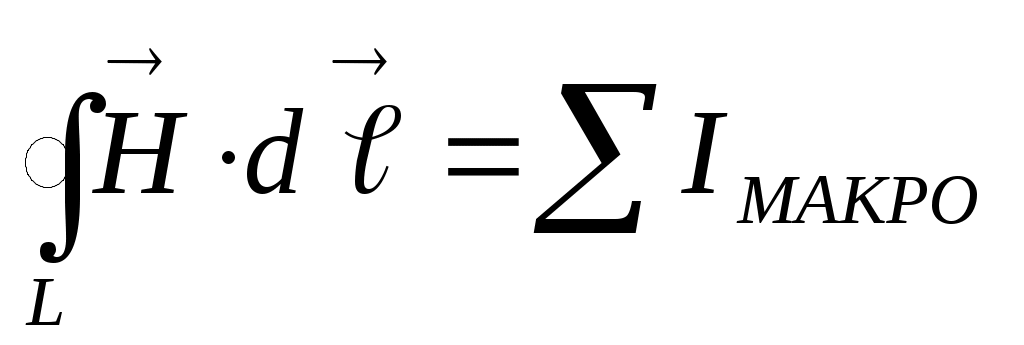. Это выражение очень удобно, так как в правой части не содержит микро- (молекулярные) токиI’, которые очень трудно оценить, и представляет собой теорему о циркуляции вектора 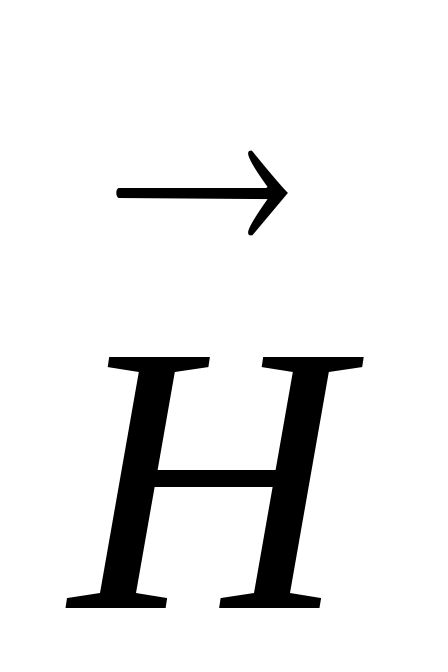: циркуляция вектора напря­женности 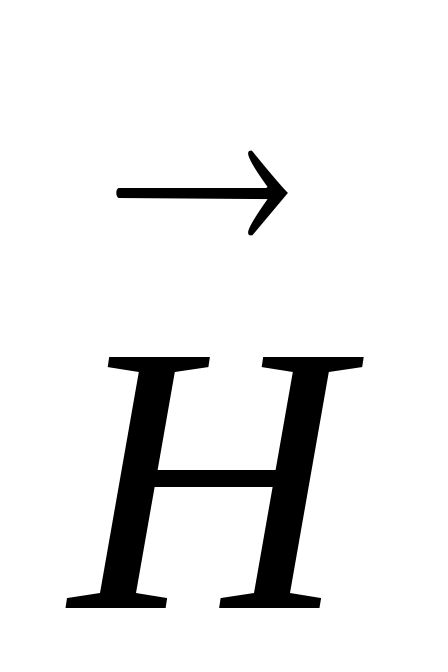магнитного поля по произвольному контуру равна алгебраической сумме макроско­пических токов, охватываемых этим контуром.

Вектор намагниченности 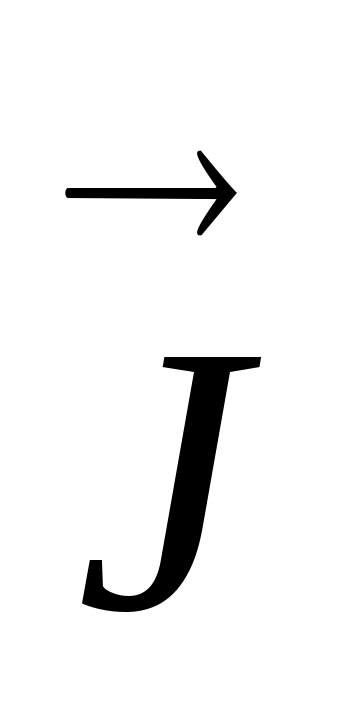принято связывать не с магнитной индукцией , а с напряженностью поля 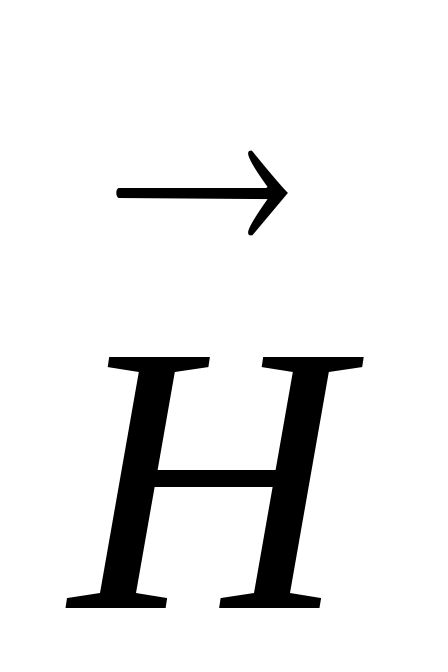: 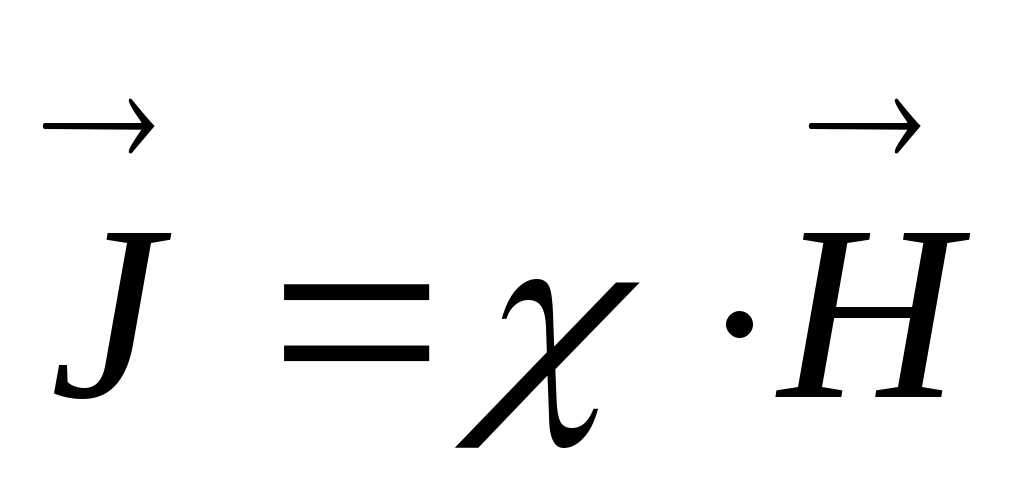, где безразмерная величина χ называется магнитной восприимчи­востью. Для диамагнетиков χ − отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков χ − положительна (поле молекулярных токов совпадает с внешним).

В диа- и парамагнетиках при не очень сильных полях χне зависит от Н и: ,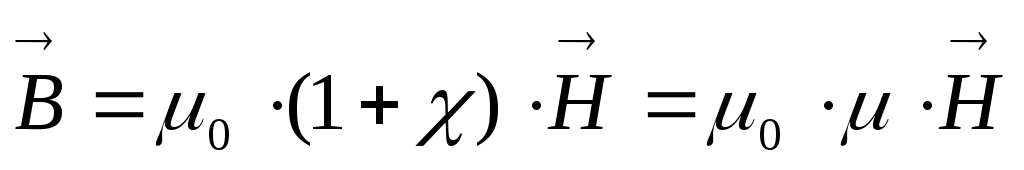

где безразмерная величина μ=1+χ называется магнитной проницаемостью вещества. μ и χ характеризуют магнитные свойства магнетиков.

Так как абсолютное значение магнитной восприимчивости χ для диа- и парамагнетиков очень мало (порядка 10^–4−10^–6), то μ для них незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков μ < 1, для парамагнетиков μ > 1, причем как у тех, так и у других μотличается от единицы весьма мало, т.е. магнитные свойства этих магнетиков выражены очень слабо.
Природа магнетизма. Ферромагнетики.

Причина усиления в парамагнетиках состоит в том, что ато­мы или молекулы вещества представляют собой магнитные дипо­ли (обладают магнитными моментами). Эти диполи ориентируются во внешнем поле вдоль силовых линий и усиливают его. Если в соленоид вставлен сердечник из пара­магнетика, то дипольные моменты ато­мов (на рис. – стрелки) ориентируются вдоль по полю. В парамагнетике этот эффект очень слаб, и μ близко к единице, так как из-за теплового движения происходит только незначительная преимущественная ориентация диполей вдоль поля (рис.а). В молекулах диамагнетиков магнитный момент отсутствует, но он появляется при помещении диамагнетика во внешнее магнитное поле. Результирующий магнитный момент в диамагнетике мал, всегда направлен против внешнего поля и от температуры не зависит.

С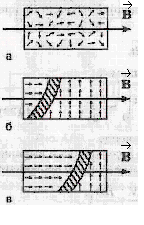
уществуют вещества, в которых μ

10

---

² ÷10³ и более. Это железо, кобальт, никель, сплавы редких металлов (иттрия и др.). Такие вещества называются ферромагнетиками. В них очень ве­лико диполь-дипольное взаимодействие, в результате чего маг­нитные диполи атомов в отдельных областях выстраиваются параллельно друг другу без всякого внешнего поля. Этот эффект носит название спонтанного(самопроизвольного) намагничива­ния.На рис. б показаны две такие области, которые по­лучили название домены. Границы между доменами называются доменными стенками (заштриховано на рис. б и в).

Если приложить внешнее магнитное поле , например, вставив кусок ферромагнетика в соленоид, то домен с благоприятной ориентацией диполей разра­стается за счет домена с неблагоприятным намагничиванием. Это происходит путем поворота диполей в тонком слое доменной стен­ки, в результате чего стенка перемещается (рис. в). Ре­зультирующее поле будет намного больше, чем без ферромагнетика. Такая катушка с железным сердечни­ком, создающая сильное поле, называется электромагнитом.

В
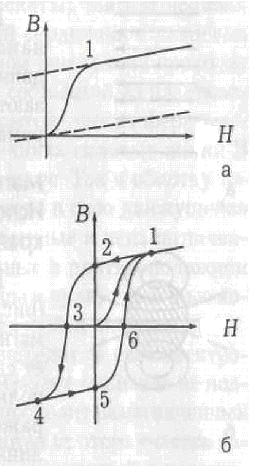
конце концов, весь объем тела превращается в один домен, наступает насыщение (точка 1 на рис. а и б). Если внешнее поле получается за счет тока во внешней катушке соленоида , то дальнейшее увеличение В будет происходить только за счет этого тока, т.е., за счет увеличения напряженности поля H . Таким образом, связь между Н и В оказы­вается нелинейной (рис. а), а μ ≠ const.

Если теперь уменьшать токв соле­ноиде, т.е., H, то В будет уменьшаться, но не до нуля, так как при H = 0 достаточно сильная остаточная индукция В_ОСТ (точка 2 на рис. б) получается за счет спон­

---

танного намагничивания куска ферро­магнетика. Этот кусок можно вынуть из катушки, он будет более или менее долго намагниченным. Это постоян­ный магнит.

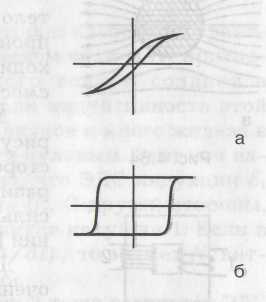
Если железный сердечник оста­вить в соленоиде, а ток соленоида пу­стить в обратную сторону, то остаточная индукция В_ОСТ исчезает при некотором отрицательном Н_К (ко­эрцитивная сила, точка 3 на рис. б). Затем будет происходить намагни­чивание до насыщения в противопо­ложном направлении (точка 4). Если снова уменьшать H до нуля и затем увеличивать в положительном на­правлении, то мы пойдем не по пути 4 → 3→ 2 → 1, а по пути 4 → 5 (остаточное намагничивание в противоположном направлении) → 6 ( положительная коэрцитивная сила Н_К) → 1. Так что зависимость Bот Н не только нелинейная, но и неоднозначная. Это явление носит на­звание гистерезиса, а получающаяся петля (рис. б) назы­вается петлей гистерезиса.

В разных материалах форма петли гистерезиса разная. На рис. показаны петли гистерезиса для чистого же­леза (а) и для сплавов, из которых делают постоянные маг­ниты (б).

При высоких температурах спонтанное намагничивание разрушается тепловым движением и ферромагнетик превращается в парамагнетик.
Энергия магнитного поля. Когда в катушке с индуктивностью L и сопротивлением течет изменяющийся ток I(t), к катушке подводится электрическая мощность:

.

Полная работа, необходимая для увеличения силы тока от нуля до I, равна:
. Эта работа равна энергии W, запасенной катуш­кой индуктивности, в которой течет ток.

Эту энергию можно рассматривать как энергию магнитного поля и выразить непосредственно через индукцию магнитного поля.

---

Действительно, подставив вместо L для индуктивности соленоида L= μ₀ μ n²V ( ),

и учитывая, что индукция магнитного поля внут­ри соленоида равна В = μ₀ μ· n·I , получим: Эта формула справедлива для однородного поля, заполняющего объем V. В самом общем случае энергия магнитного поля, локализованного в некотором объеме пространства, определяется как: , где – объемная плотность энергии (энергия в единице объема ).

---

2.6. ОСНОВЫ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.
Вихревое электрическое поле

Из электростатики мы знаем, что электрическое поле создается электрическими зарядами Q, cиловые линии такого поля не замкнуты, а циркуляция вектора ( обозначим его ) равна нулю: . С другой стороны, в явлении электромагнитной индукции изменяющееся магнитное поле приводит к э.д.с. ε_инд , т.е., к появлению электрического поля (обозначим его ),: . Сравнивая эти два выражения , видим, что между рассматриваемыми полями ( и ) имеется принципиальное различие: циркуляция вектора ,в отличие от циркуляции вектора , не равна нулю.

Следовательно, электрическое поле , порождаемое магнитным полем, как и само магнитное поле, является полем с замкнутыми силовыми линиями, т. е. вихревым электрическим полем. Таким образом, электрическое поле может создаваться электрическими зарядами и переменными магнитными полями. Это утверждение в общем виде записывают как: .

Ток смещения

Согласно Максвеллу, если всякое переменное магнитное поле

---