Файл: Мазмны Кiрiспе 1 тарау. Геометриялы салулар теориясыны кейбiр мселелерi 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 224
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 десек, ОА1 – ізделінді кесінді.
V
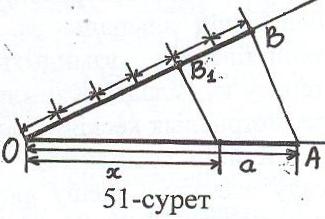
. х =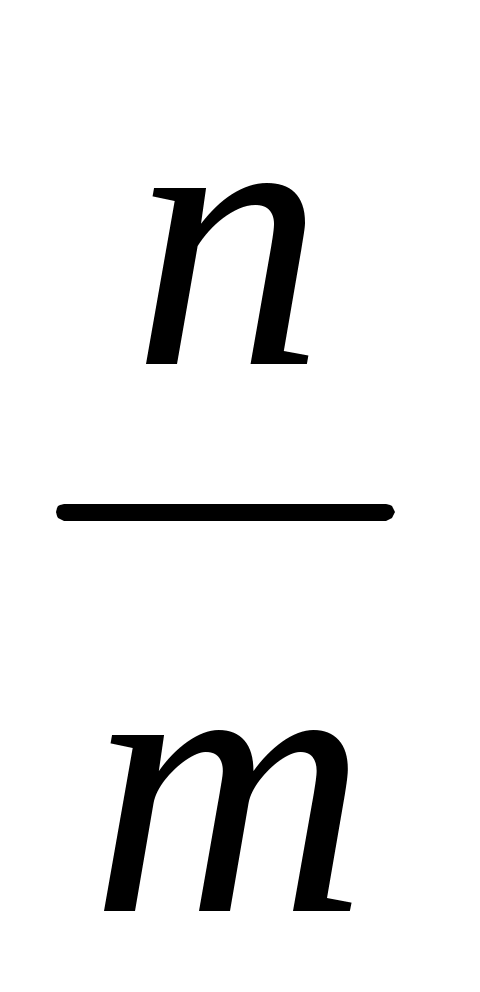 a, n, m – берілген натурал сандар, а – берілген кесінді. Бұл кесіндіні екі әдіспен салуға болады:
a, n, m – берілген натурал сандар, а – берілген кесінді. Бұл кесіндіні екі әдіспен салуға болады:
1) а кесіндісін бірдей m бөлікке бөліп (жо-
ғардағы ІV салу), алынған кесіндіні n есе
үлкейтеміз (ІІІ салу).
2) Айталық ОА = a. О нүктесінен шығатын
кез – келген сәулеге ОВ1 = nв және ОВ = mв
кесінділерін салып (51-сурет), В1 нүктесі ар-
қылы АВ – ға параллель А1В1 кесіндісін
жүргіземіз (А1 ОА). Сонда ОА1 кесіндісі ізделінді болады, яғни х = ОА1.
V
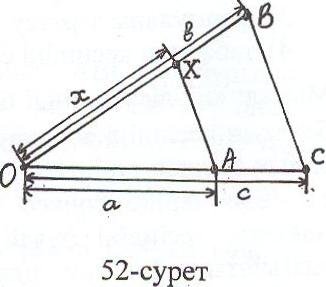
І. х =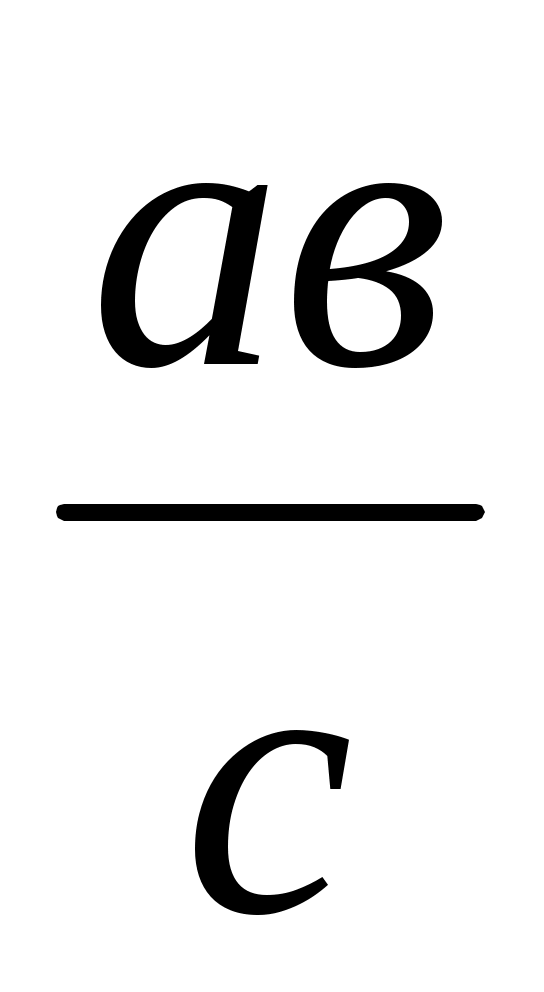 (берілген үш кесіндіге пропорционал төртінші кесіндіні салу).
(берілген үш кесіндіге пропорционал төртінші кесіндіні салу).
Берілген шартты с:а = в:х пропорциясытүрінде
жазып аламыз. Айталық ОА=а, ОС=с кесінділері
О нүктесінен шығатын бір сәуле бойында жатыр,
яғни ОА, ОС – бір қатынастың «мүшелері» (52 -
сурет). О нүктесінен шығатын екінші сәулеге
екінші қатынастың белгілі мүшесін, яғни ОВ = в
кесіндісін саламыз. А нүктесі арқылы өтіп, ВС–ға
параллель болатын түзудің ОВ – мен қиылысу нүктесі Х болса, онда ОХ – ізделінді кесінді.
VІІ. х =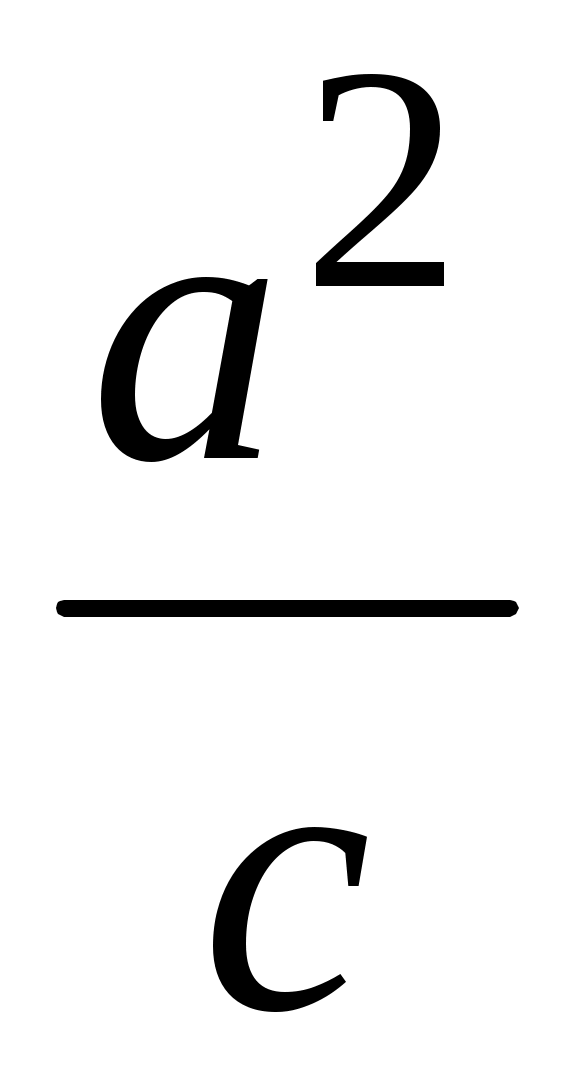 . І әдіс: в = а деп алып, жоғардағы VІ салу орындалады.
. І әдіс: в = а деп алып, жоғардағы VІ салу орындалады.
І
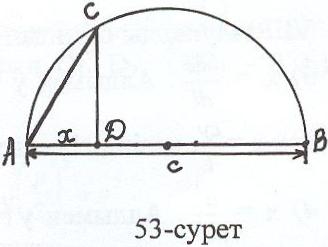
І әдіс: (бұл әдіс а < с болғанда қолданылады) диаметрі АВ = c болатын жарты шеңбер тұрғызып, оның ω (А, а) шеңберімен
қиылысуын С деп белгілейміз (53 – сурет).
Содан соң С нүктесінен АВ–ға перпендикуляр
жүргізсек, АD – ізделінді кесінді болады (D –
перпендикулярдың табаны), яғни х = AD.
VІІІ. х =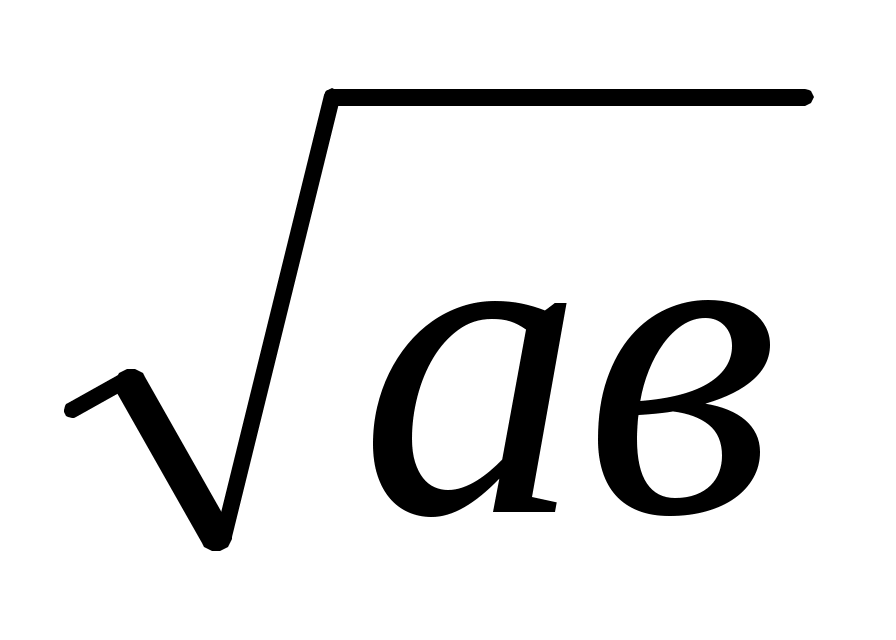 (берілген екі кесіндінің пропорционал ортасын салу).
(берілген екі кесіндінің пропорционал ортасын салу).
І
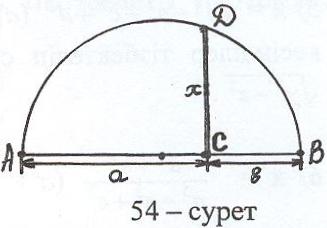
әдіс: АВ = а + в болатын АС = а, СВ = в кесінділерін салып (54-сурет), АВ диаметрі болатын шеңбер жүргіземіз және С
нүктесі арқылы АВ – ға перпендикуляр тұр -
ғызамыз. Осы перпендикуляр мен жарты шең-
бердің қиылысуын D десек, СD – ізделінді
кесінді болады, яғни х = CD.
І
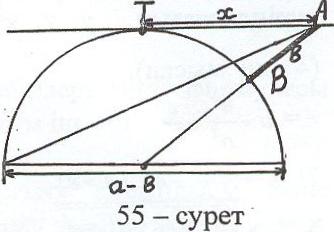
І әдіс: (а в жағдайы үшін). Диаметрі а – в болатын шеңбер салып, оның центрі арқылы қиюшы жүргіземіз (55-сурет).
Осы қиюшының шеңбер сыртындағы бөлігіне
шеңбермен қиылысу нүктесінен бастап в – ға
тең кесіндіні белгілейміз де, табылған нүкте
(кесіндінің екінші ұшы) арқылы шеңберге АТ
жанамасын жүргіземіз (Т – жанасу нүктесі).
Сонда х = АТ.
І
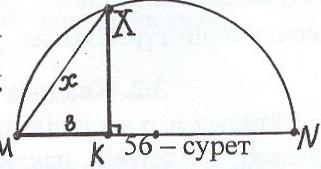
ІІ әдіс: (а в жағдайы үшін). Диаметрі MN = a шеңбер салып, MN кесінді-сіне МК = в кесіндісін белгілейміз (56-сурет).
Содан соң К нүктесі арқылы MN–ға перпен -
дикуляр тұрғызып, оның шеңбермен қимасын
Х деп белгілесек, МХ ізделінді кесінді болады,
яғни х = МХ.
ІХ. х =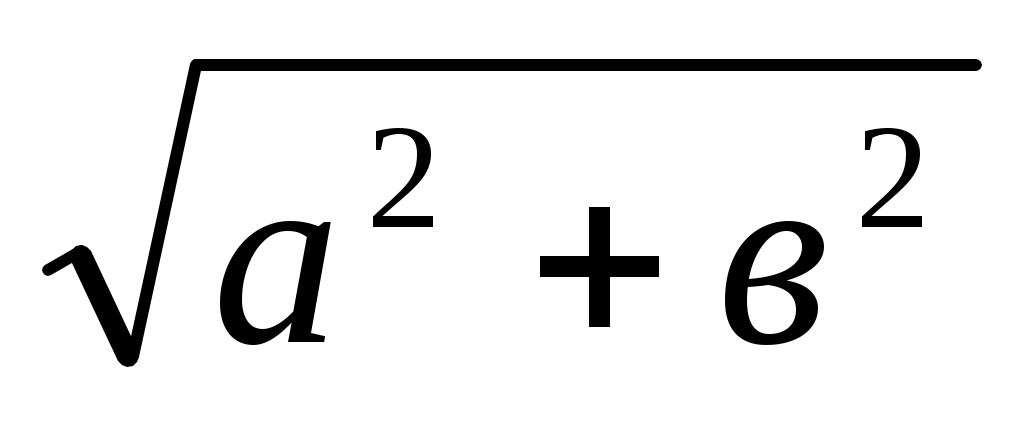 . Бұл кесінді катеттері а және в болатын тікбұрышты үшбұрыштың гипотенузасы ретінде салынады.
. Бұл кесінді катеттері а және в болатын тікбұрышты үшбұрыштың гипотенузасы ретінде салынады.
Х. х =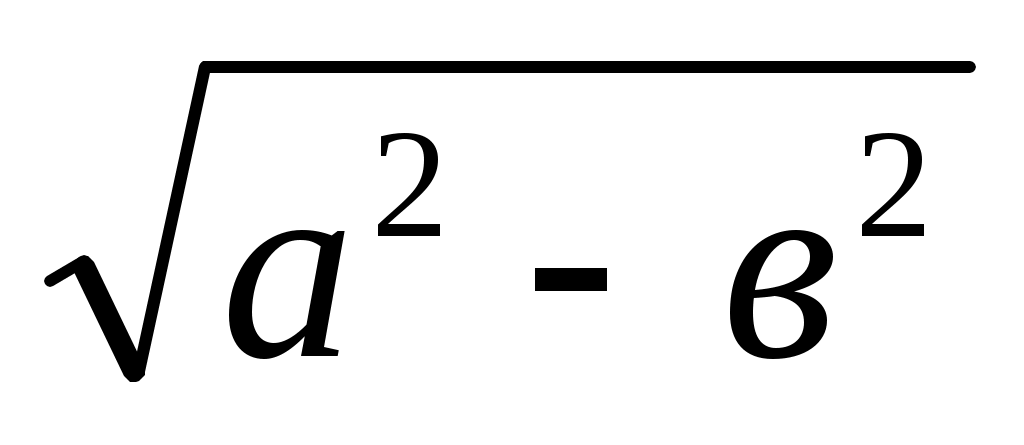 . х кесіндісі гипотенузасы а, бір катеті в болатын тікбұрышты үшбұрыштың екінші катеті болады.
. х кесіндісі гипотенузасы а, бір катеті в болатын тікбұрышты үшбұрыштың екінші катеті болады.
Кейбір есептерде кесінді күрделі формулалармен беріледі. Оларды шешу үшін қарапайым түрге келтіру керек. Мысалдар қарастырайық:
1) х = а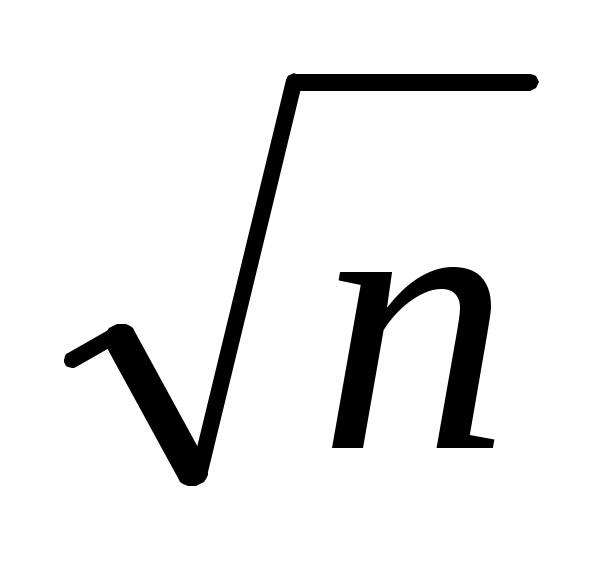 , n Ν. Егер n = p∙q (мұндағы p, q Ν) болса, онда х =
, n Ν. Егер n = p∙q (мұндағы p, q Ν) болса, онда х = 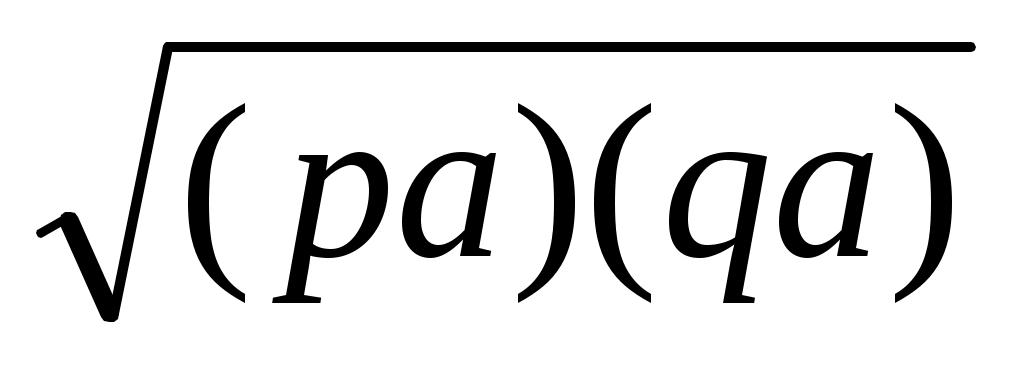 деп жазып аламыз да, жоғардағы VIII салуды қолданамыз. Егер n = p2+ q2болса, онда х =
деп жазып аламыз да, жоғардағы VIII салуды қолданамыз. Егер n = p2+ q2болса, онда х = 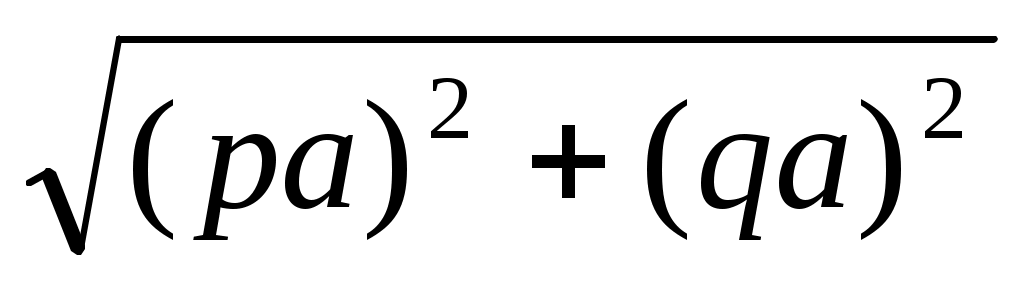 болады да, ІХ салу орындалады. Ал егер n=p2-q2 болса, онда х =
болады да, ІХ салу орындалады. Ал егер n=p2-q2 болса, онда х = 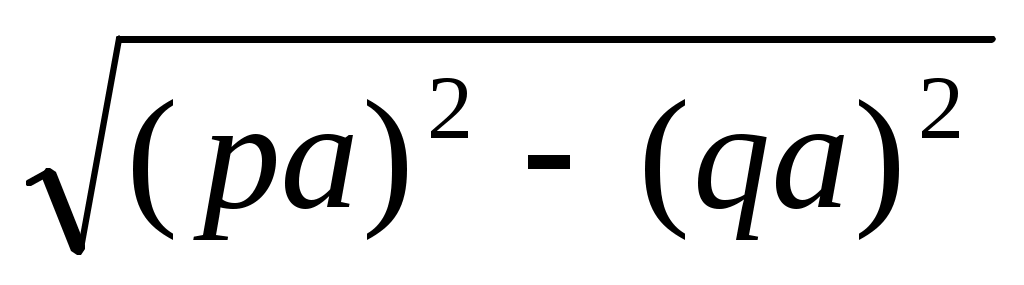 , яғни Х салу орындалады.
, яғни Х салу орындалады.
2) х = a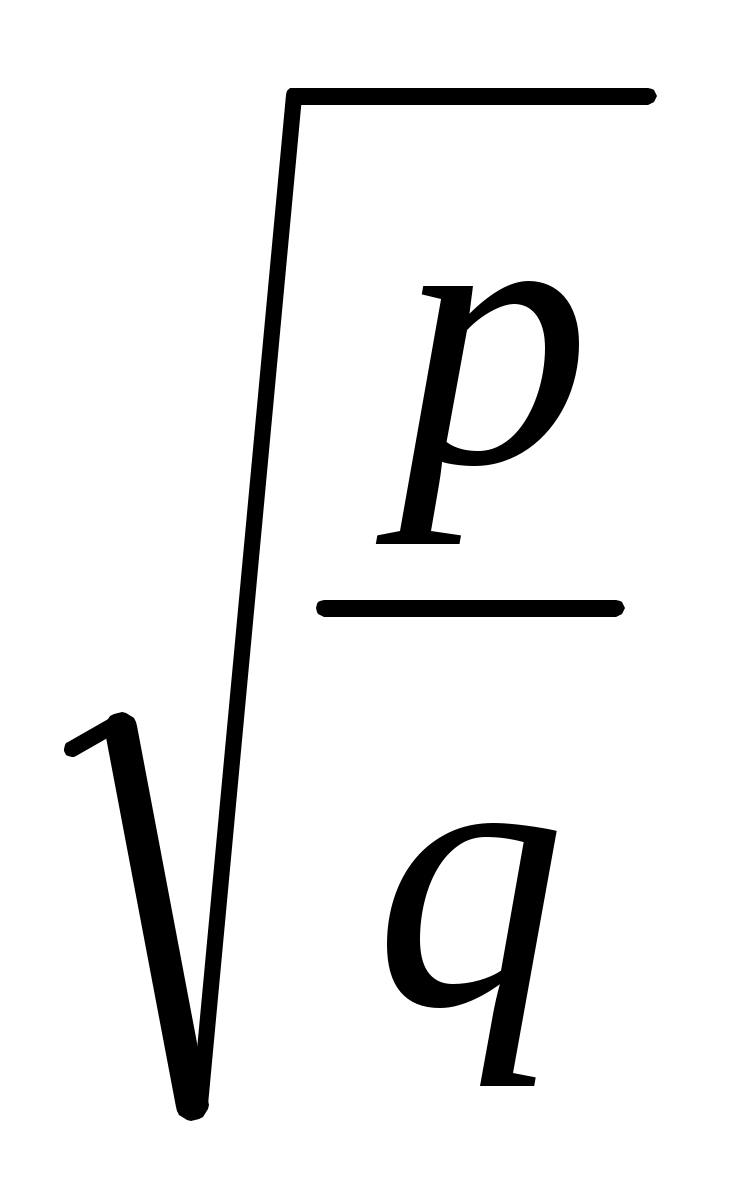 , p, q Ν. Бұл теңдікті х =
, p, q Ν. Бұл теңдікті х = 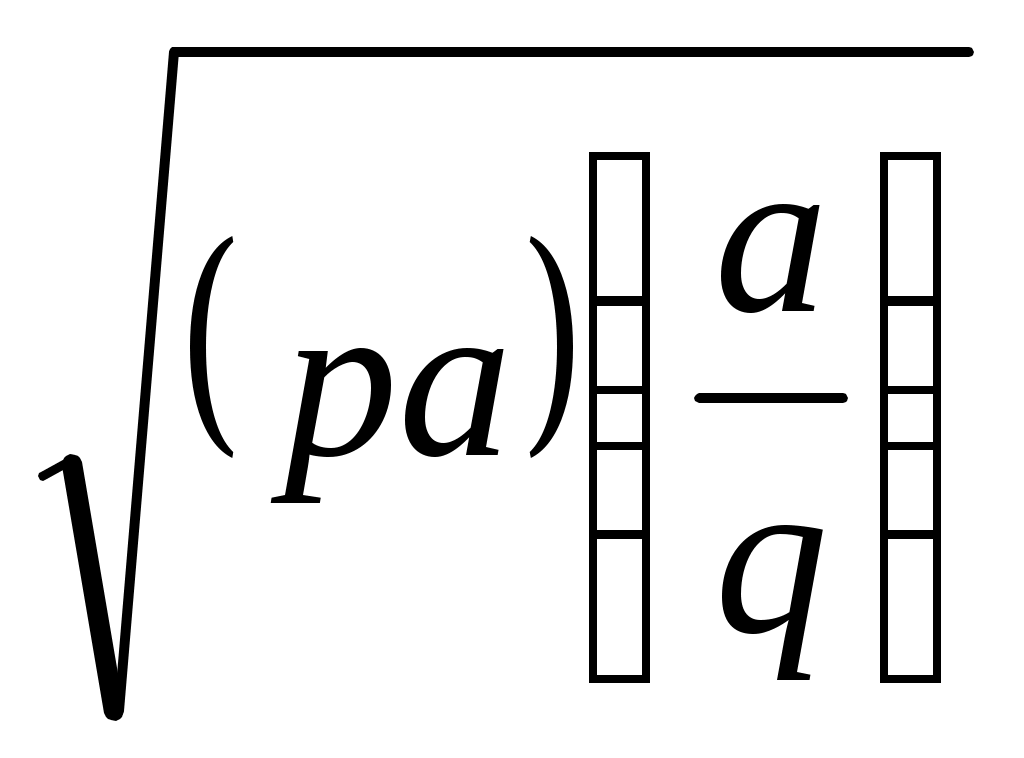
түрінде жазып, V және VІІІ салуларды орындаймыз.
3) х =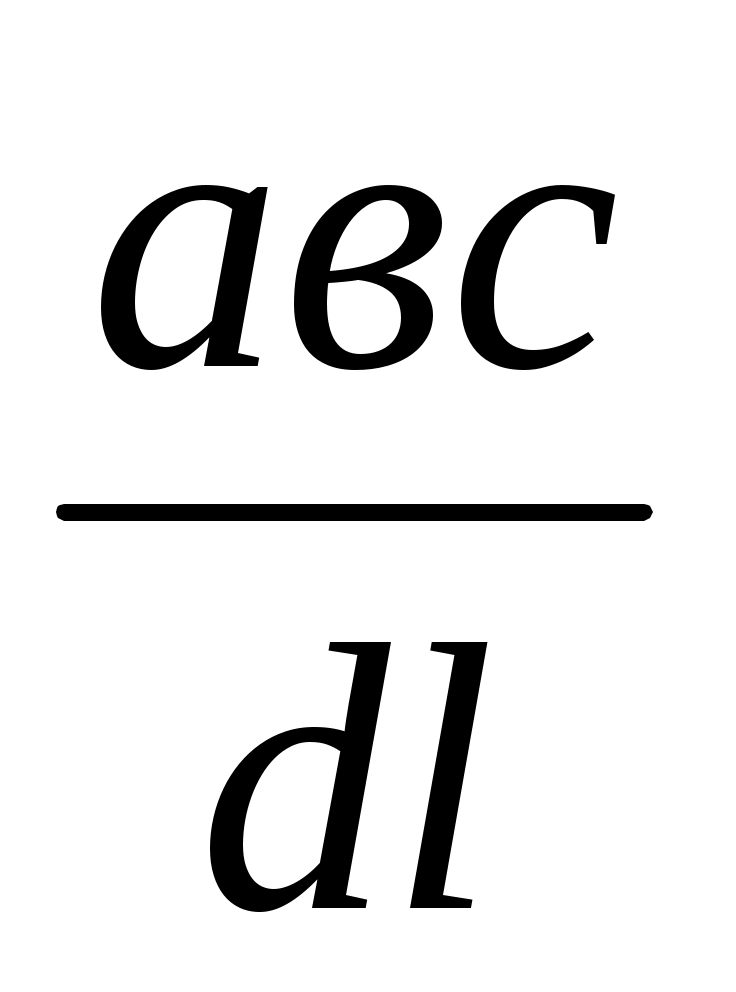 . Алдымен у =
. Алдымен у = 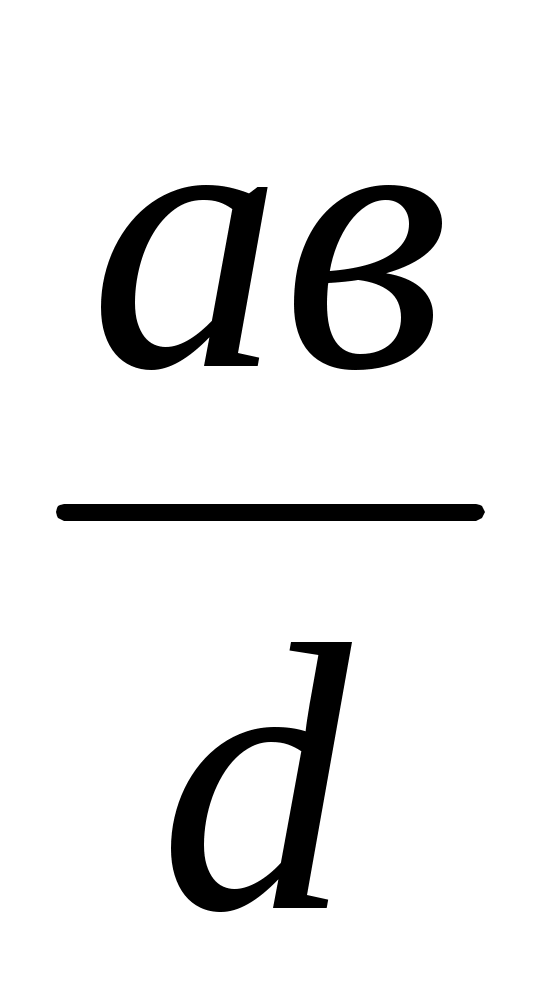 формуласы бойынша у кесіндісі, содан соң х =
формуласы бойынша у кесіндісі, содан соң х =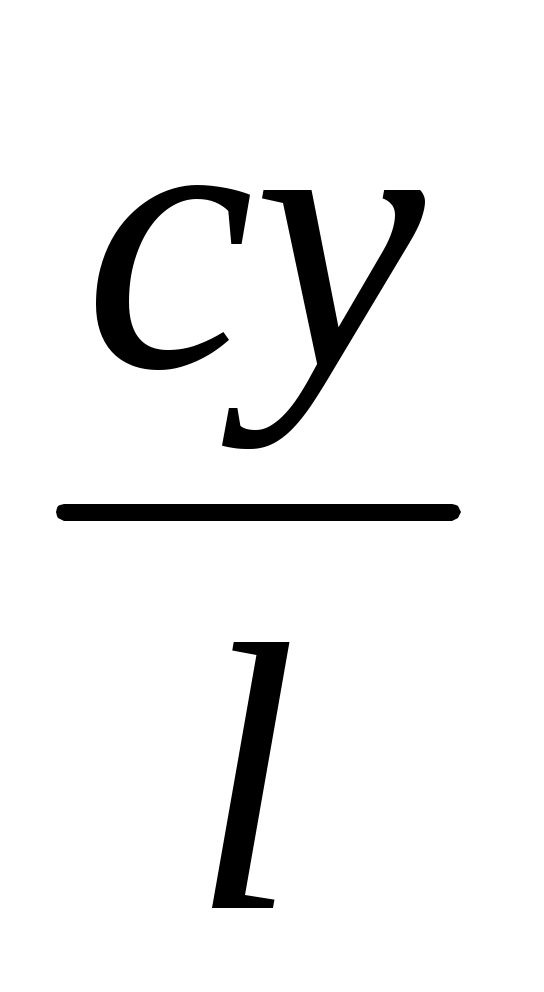 кесіндісі салынады (VІ салу).
кесіндісі салынады (VІ салу).
4) х =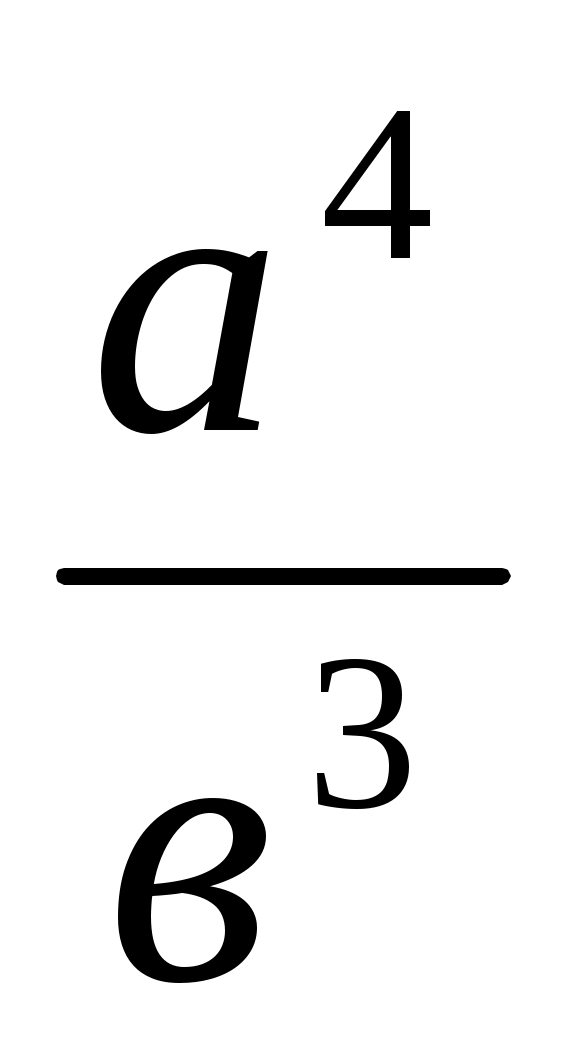 . Алдымен у =
. Алдымен у = 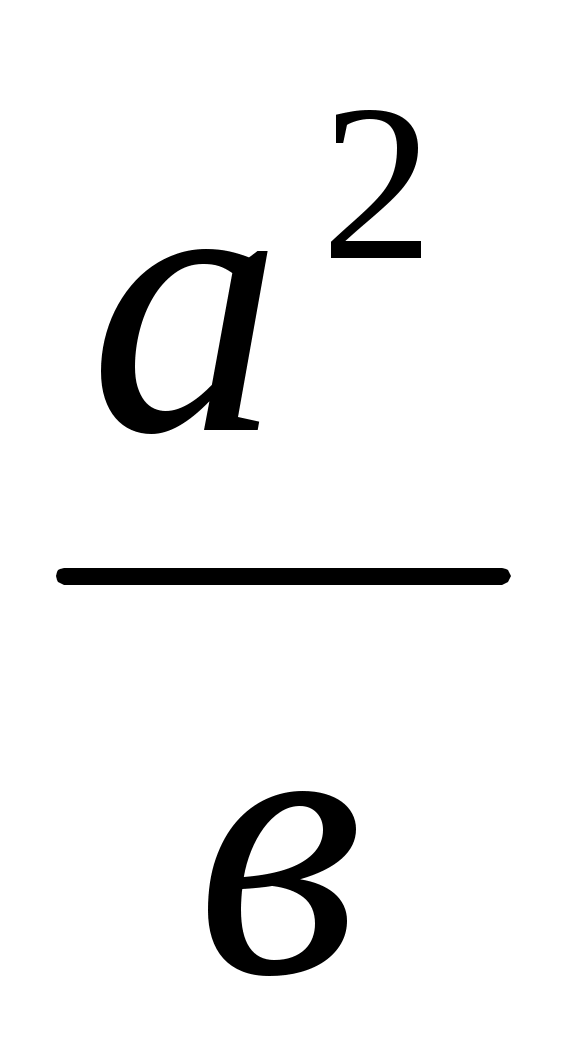 кесіндісі (VІІ салу), содан соң х =
кесіндісі (VІІ салу), содан соң х = 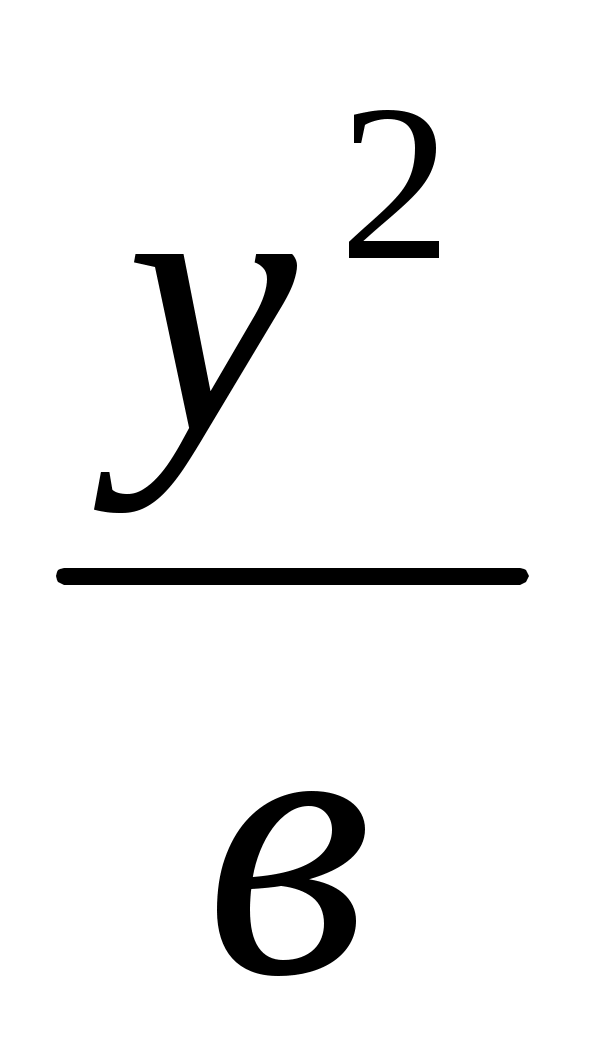 кесіндісі тұрғызылады.
кесіндісі тұрғызылады.
5) х =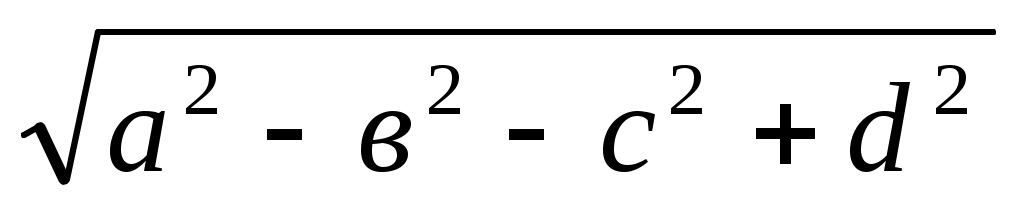 (а2 + d2 в2 + с2). Бұл кесіндіні салу үшін мына кесінділер тізбектеліп салынады: у =
(а2 + d2 в2 + с2). Бұл кесіндіні салу үшін мына кесінділер тізбектеліп салынады: у = 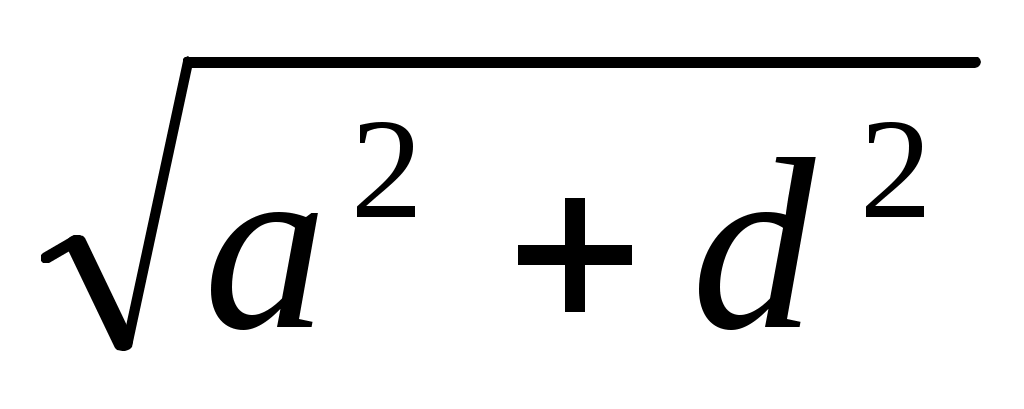 , z =
, z = 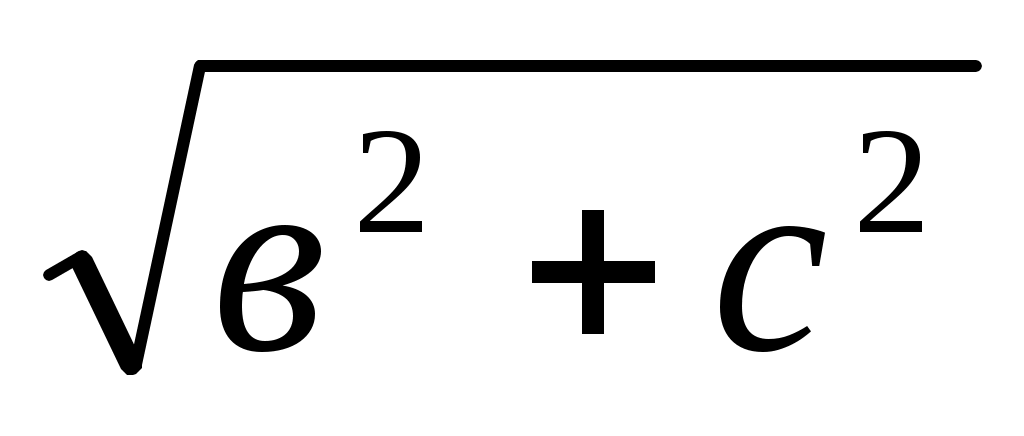 , x =
, x = 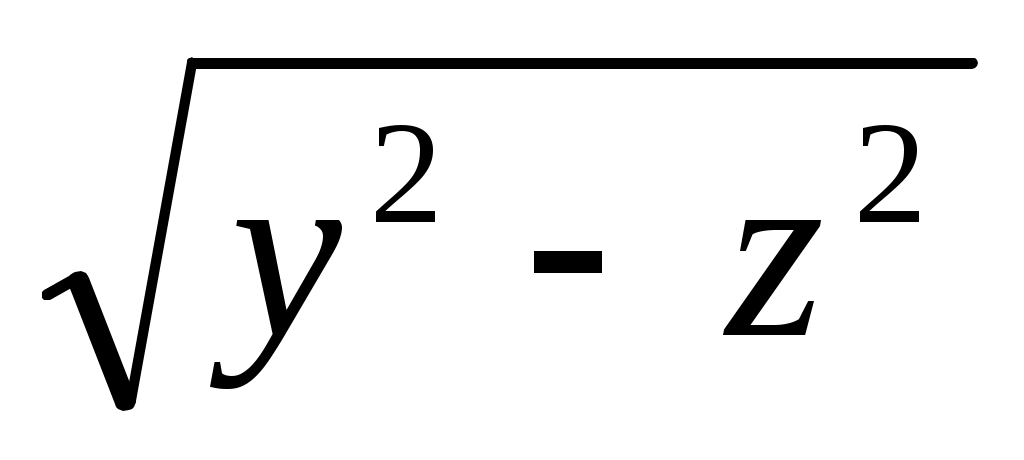 .
.
6) х =
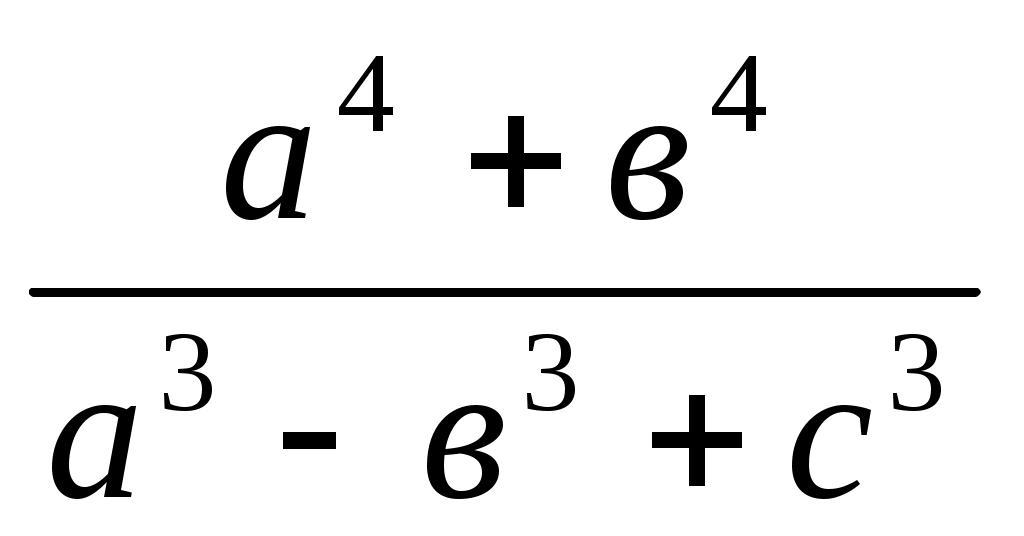 (а3+ с3 в3). Берілген теңдікті х =
(а3+ с3 в3). Берілген теңдікті х = 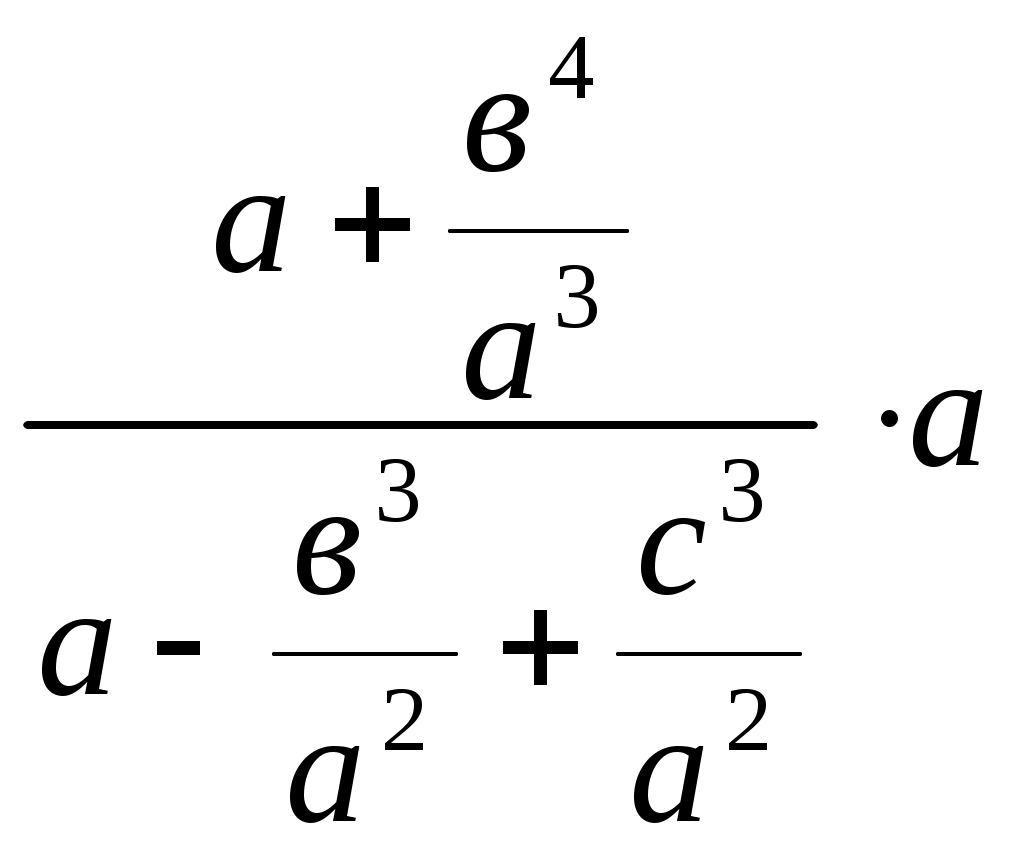 түрінде жазып, у, z, х кесінділерін ретімен саламыз: y = a+
түрінде жазып, у, z, х кесінділерін ретімен саламыз: y = a+ 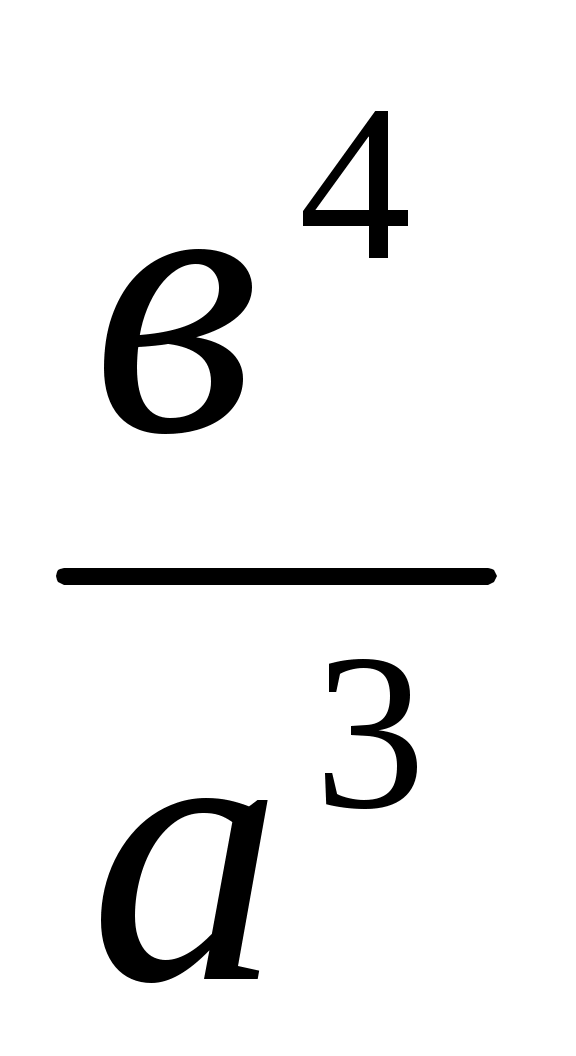 (4 - ші мысал),
(4 - ші мысал),
z =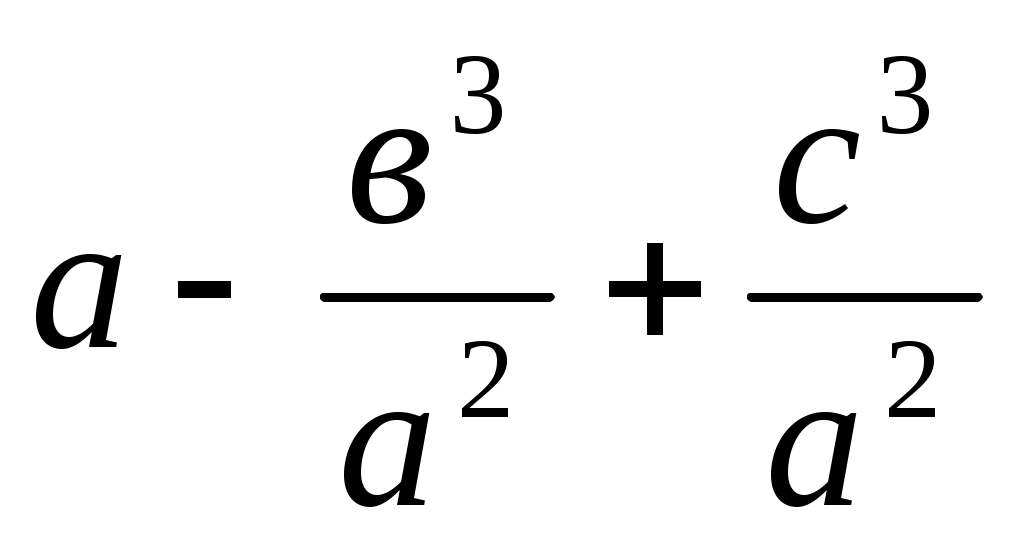 (3 - ші мысал), х =
(3 - ші мысал), х = 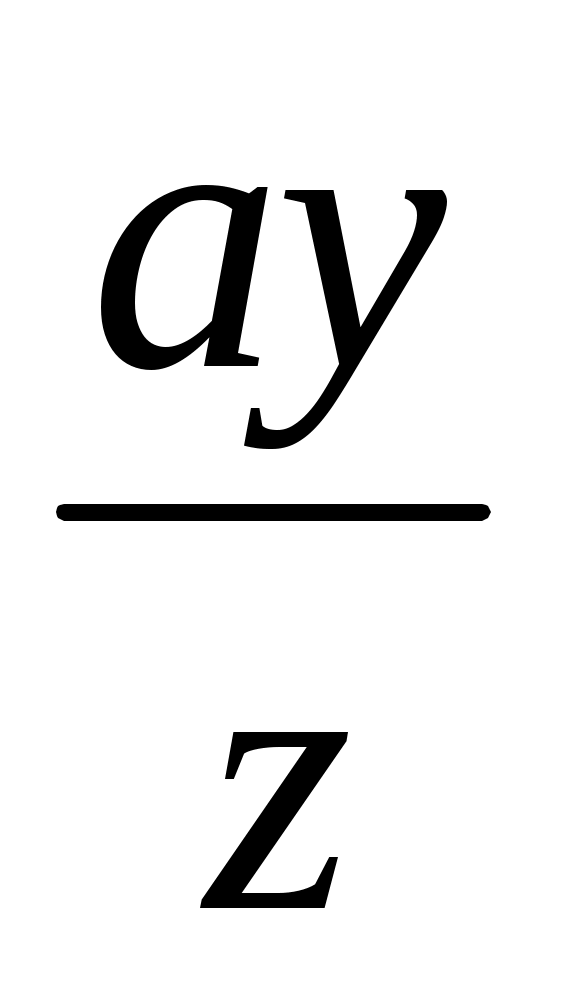 (ІV салу).
(ІV салу).
7) х =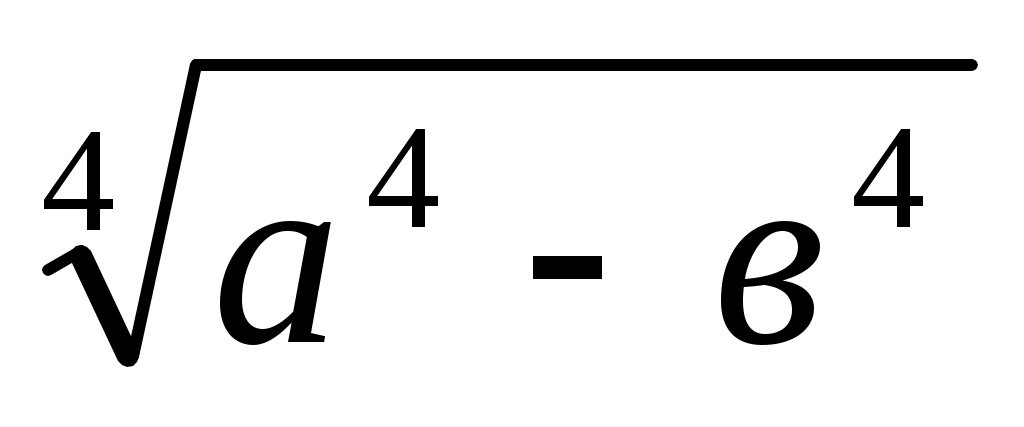 (а в).
(а в).
х =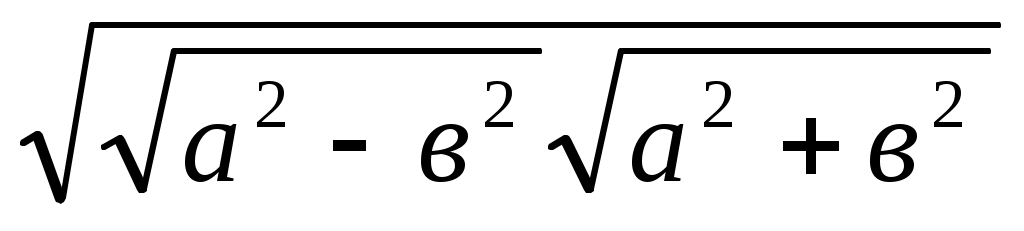 теңдігі бойынша жоғардағы Х, ХІ және VІІІ салуларды пайдаланып, сәйкесінше у =
теңдігі бойынша жоғардағы Х, ХІ және VІІІ салуларды пайдаланып, сәйкесінше у =  , z =
, z = 
, x =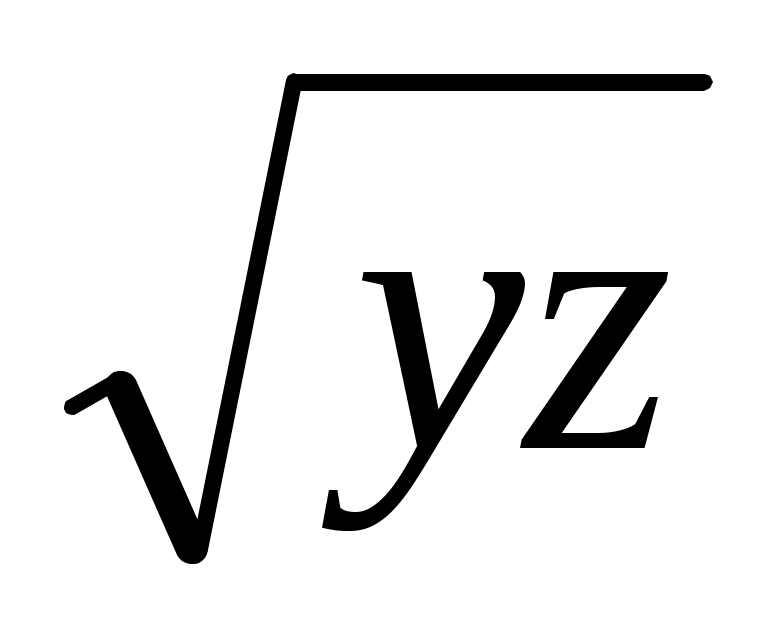 кесінділерін тұрғызамыз.
кесінділерін тұрғызамыз.
3.2. Квадрат теңдеудің түбірлерін тұрғызу
Айталық p және q кесінділері берілген. Ұзындығы х2 рх q2 = 0 квадрат теңдеуінің нақты түбірлеріне тең болатын кесіндіні есептемей – ақ салатындай ереже жасауға болады. Мұндағы х2 рх q2 = 0 теңдігі тіктөртбұрыш (рх) пен екі квадраттың (х2 & q2) аудандарының байланысы түрінде жазылғандықтан, босмүшені q емес, q2 түрінде жазамыз.
Көрсетілген есепті шешу үшін Виет формуласын немесе квадрат теңдеудің түбірлерінің формуласын қолдануға болады. Екі әдісті де қарастырайық:
І әдіс:
1) х2 - рх + q2 = 0 теңдеуі үшін
х1 =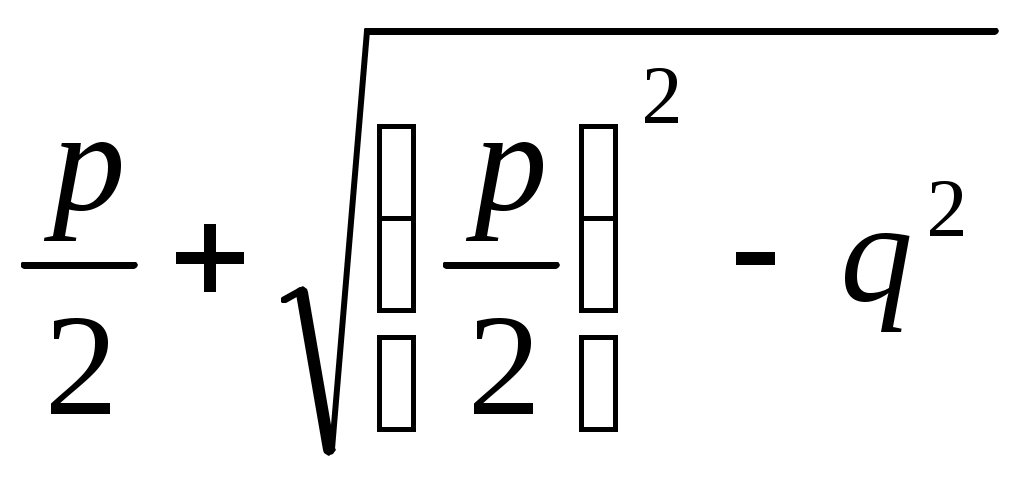 , x2 =
, x2 = 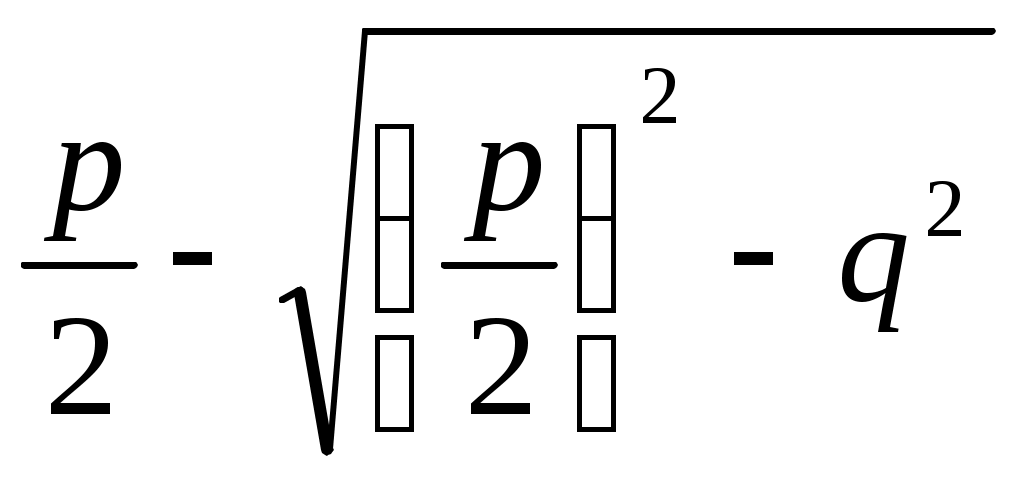 .
.
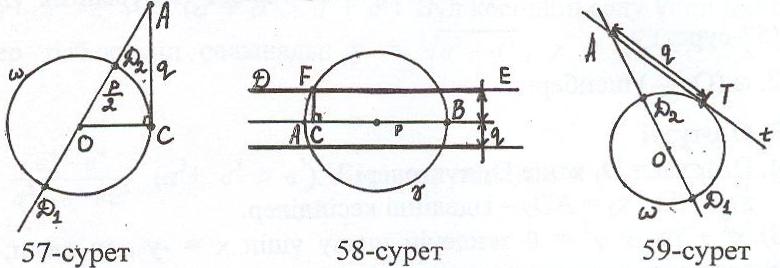
Гипотенузасы ОА =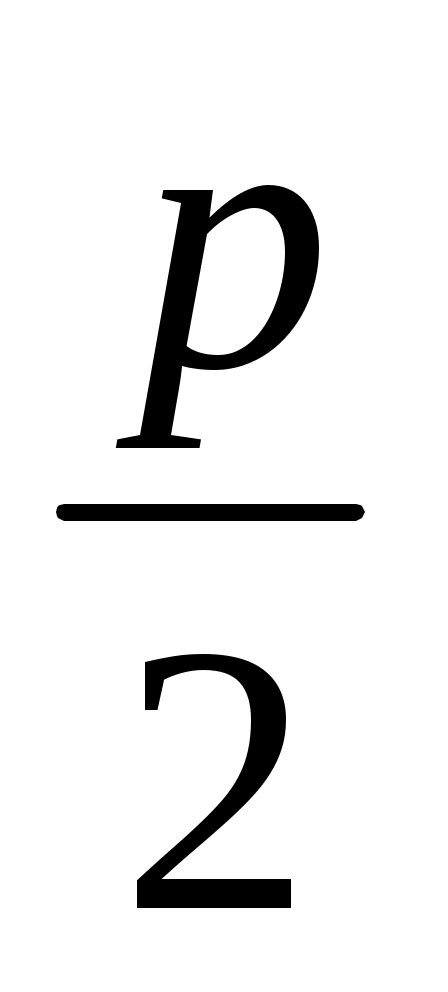 , катеті АС = q болатын тікбұрышты үшбұрыш салып (57-сурет), (О, ОС) шеңберін тұрғызамыз. Содан соң ОА түзуін жүргізіп, оның шеңберімен қимасын D1, D2 (АD1 АD2) десек, х1 = AD1, x2 = AD2.
, катеті АС = q болатын тікбұрышты үшбұрыш салып (57-сурет), (О, ОС) шеңберін тұрғызамыз. Содан соң ОА түзуін жүргізіп, оның шеңберімен қимасын D1, D2 (АD1 АD2) десек, х1 = AD1, x2 = AD2.
2) х2 - рх - q2 = 0 теңдеуі үшін
х1 =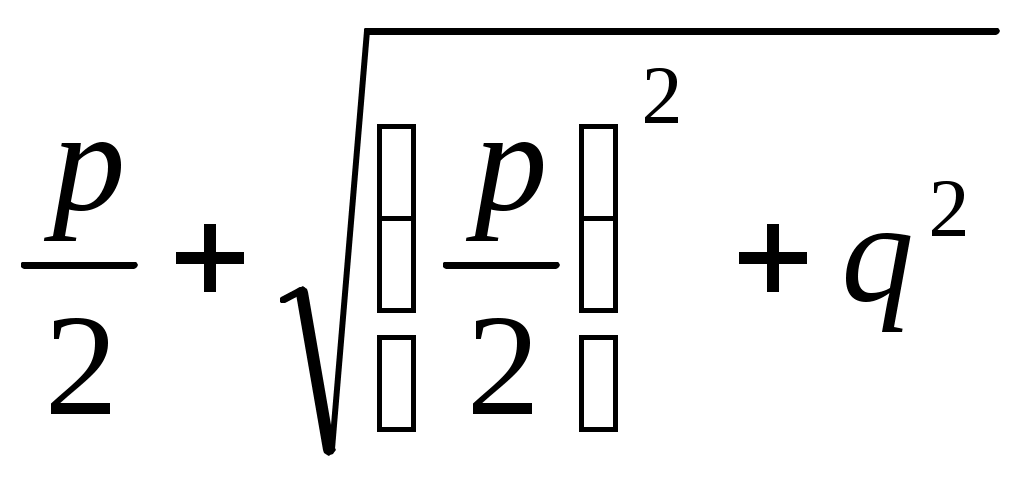 , x2 =
, x2 = 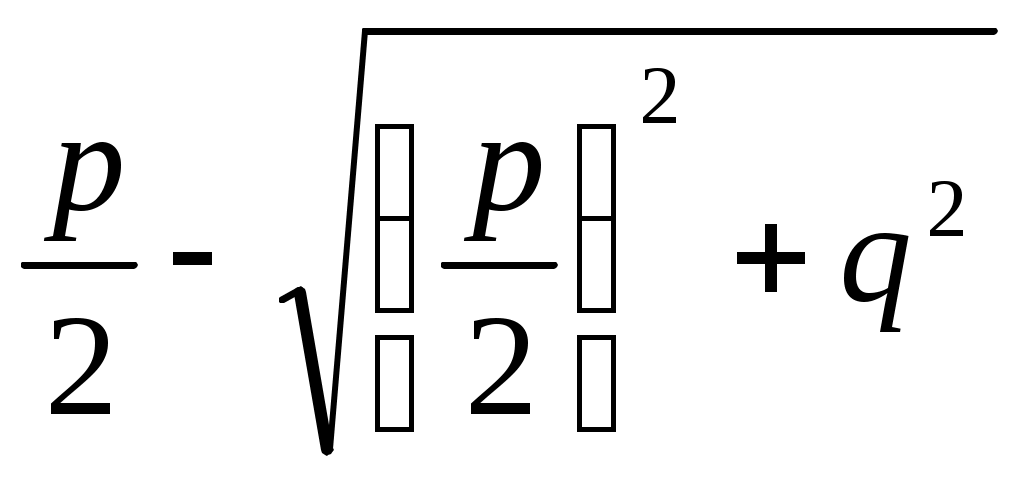 .
.
Бұл жағдайда салу жоспары төмендегіше болады:
1. ОС =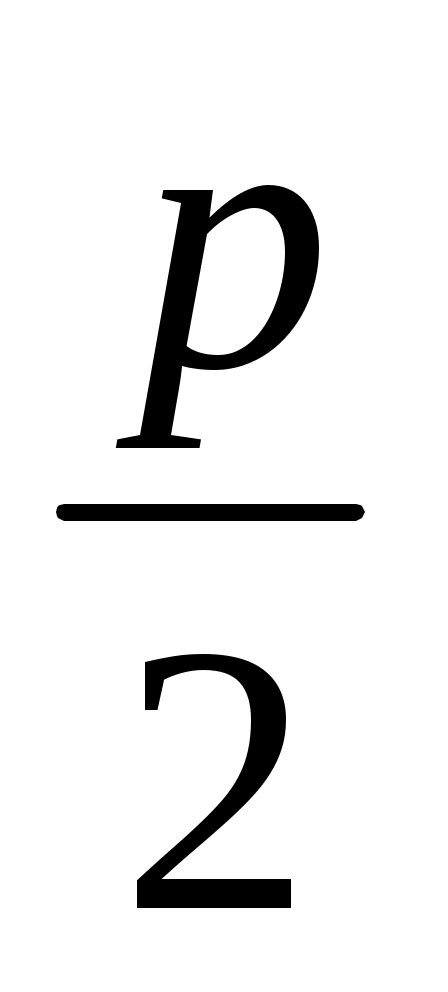 , CA =q катеттері бойынша ОСА тікбұрышты үшбұрышы (57-сурет)
, CA =q катеттері бойынша ОСА тікбұрышты үшбұрышы (57-сурет)
2. (О,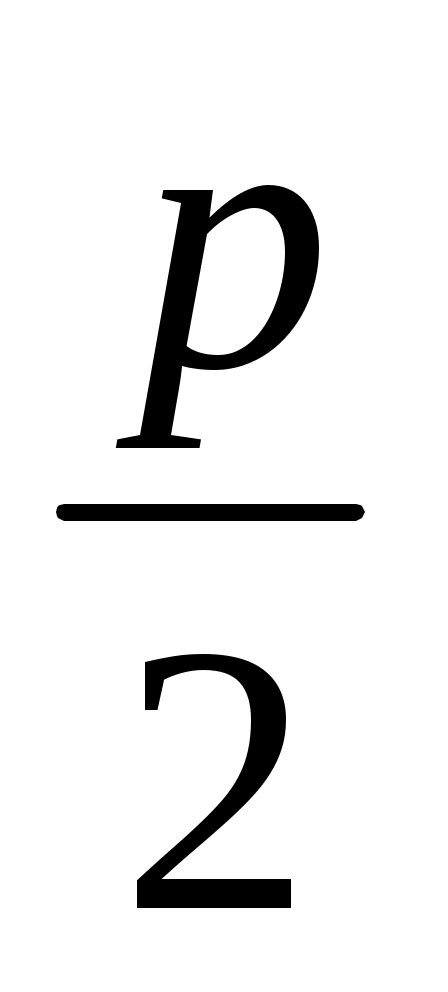 ) шеңбері
) шеңбері
3. ОА түзуі
4. ОА = D1 және D2 нүктелері
х1 = AD1, x2 = AD2 – ізделінді кесінділер.
3) х2 + рх q2 = 0 теңдеуін шешу үшін х = -у деп алып, жоғарда көрсетілген салуларды қолданамыз.
ІІ әдіс: ( Виет формуласы арқылы шешу)
1) Талдау: х2 - рх + q2 = 0 теңдеуінің түбірлері Виет формуласы бойынша мынандай байланыста болады:
х1 + х2 = р, х1 х2 = q2.
Сонда квадрат теңдеудің түбірлерін тұрғызу қосындысы және геометриялық ортасы берілген екі кесіндіні салу есебіне келеді.
Салу: 1. Диаметрі АВ = р болатын шеңбері (58-сурет)
2. АВ диаметрінен q қашықтықтағы DЕ параллель түзуі
3. DЕ = Ғ нүктесі
4. ҒС АВ және С АВ түзуі
х1 = AС, x2 = ВС – ізделінді кесінділер.
Зерттеу: Салу жоспарының үшінші қадамындағы DЕ түзуі (О, ) шеңберін q
) шеңберін q 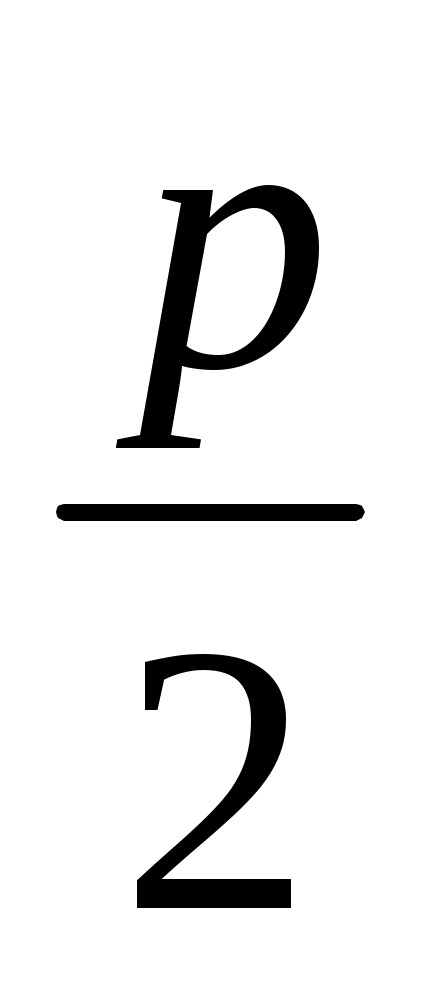 шарты орындалғанда ғана қияды. Бұл жағдайда есептің әр түрлі екі шешімі болады. Егер q =
шарты орындалғанда ғана қияды. Бұл жағдайда есептің әр түрлі екі шешімі болады. Егер q = 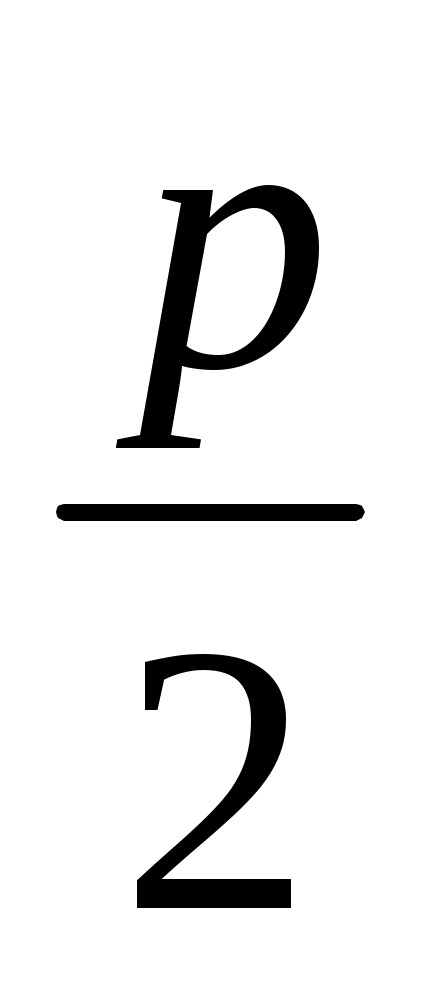 болса, DЕ түзуі шеңберін жанайды да, АС = ВС
болса, DЕ түзуі шеңберін жанайды да, АС = ВС
болады. Сондықтан х1 = х2, яғни есептің жалғыз шешімі болады. Егер q 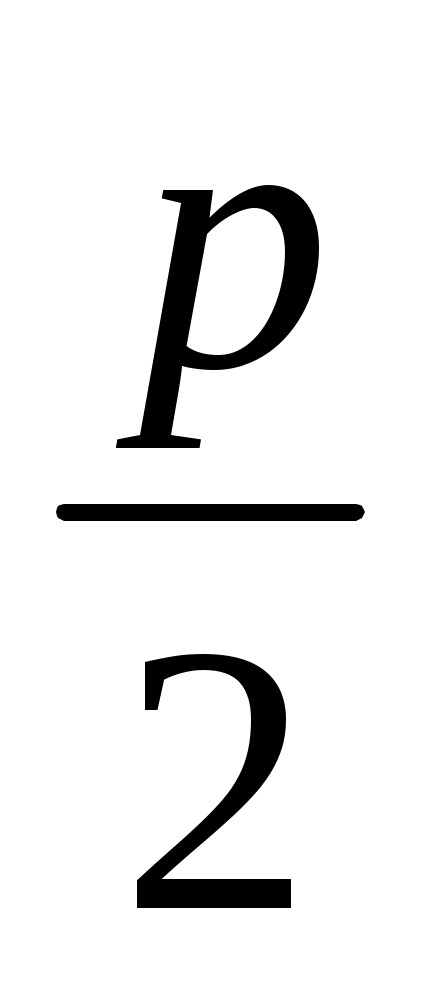 болса, DЕ түзуінің шеңберімен ортақ нүктесі болмайды да, есептің шешімі жоқ делінеді.
болса, DЕ түзуінің шеңберімен ортақ нүктесі болмайды да, есептің шешімі жоқ делінеді.
2) х2 - рх - q2 = 0 теңдеуінің түбірлері х1 + х2 = р, х1 х2 = - q2 шарттары арқылы байланысқан. Бұдан бір түбірі оң (айталық х1), ал екіншісі теріс (яғни х2) екені көрініп тұр. Олай болса, х1 = х1, х2 =-х2. Сондықтан х1 -х2= p, x1 х2= q2. Сонымен бұл айырмасы және геометриялық ортасы берілген екі кесіндіні салу есебіне келеді. Салу жоспары былайша болады: (59-сурет)
1) (О, ) шеңбері
) шеңбері
2) кез – келген Т нүктесінен t жанамасы
3) ТА = q болатындай А t нүктесі
4) ОА түзуі
5) ОА = D1, D2 (AD1 AD2) нүктелері
AD1, AD2 – ізделінді кесінділер, яғни х1 = AD1, x2 = AD2.
3.3. Тригонометриялық функциялар арқылы өрнектелген кесіндіні салу
Берілген бұрыштың тригонометриялық функциясына байланысты кесінділерді сызғыш пен циркульды пайдаланып салуға болады. Мысалдар қарастырайық:
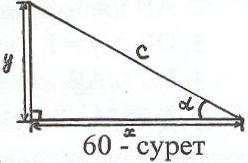
1-мысал: с кесіндісі және сүйір бұрышы
берілген. х = c cos, y = c sin формулала -
рымен берілген х,у кесінділерін салу керек.
Ол үшін
V

. х =
1) а кесіндісін бірдей m бөлікке бөліп (жо-
ғардағы ІV салу), алынған кесіндіні n есе
үлкейтеміз (ІІІ салу).
2) Айталық ОА = a. О нүктесінен шығатын
кез – келген сәулеге ОВ1 = nв және ОВ = mв
кесінділерін салып (51-сурет), В1 нүктесі ар-
қылы АВ – ға параллель А1В1 кесіндісін
жүргіземіз (А1 ОА). Сонда ОА1 кесіндісі ізделінді болады, яғни х = ОА1.
V

І. х =
Берілген шартты с:а = в:х пропорциясытүрінде
жазып аламыз. Айталық ОА=а, ОС=с кесінділері
О нүктесінен шығатын бір сәуле бойында жатыр,
яғни ОА, ОС – бір қатынастың «мүшелері» (52 -
сурет). О нүктесінен шығатын екінші сәулеге
екінші қатынастың белгілі мүшесін, яғни ОВ = в
кесіндісін саламыз. А нүктесі арқылы өтіп, ВС–ға
параллель болатын түзудің ОВ – мен қиылысу нүктесі Х болса, онда ОХ – ізделінді кесінді.
VІІ. х =
І

І әдіс: (бұл әдіс а < с болғанда қолданылады) диаметрі АВ = c болатын жарты шеңбер тұрғызып, оның ω (А, а) шеңберімен
қиылысуын С деп белгілейміз (53 – сурет).
Содан соң С нүктесінен АВ–ға перпендикуляр
жүргізсек, АD – ізделінді кесінді болады (D –
перпендикулярдың табаны), яғни х = AD.
VІІІ. х =
І

әдіс: АВ = а + в болатын АС = а, СВ = в кесінділерін салып (54-сурет), АВ диаметрі болатын шеңбер жүргіземіз және С
нүктесі арқылы АВ – ға перпендикуляр тұр -
ғызамыз. Осы перпендикуляр мен жарты шең-
бердің қиылысуын D десек, СD – ізделінді
кесінді болады, яғни х = CD.
І

І әдіс: (а в жағдайы үшін). Диаметрі а – в болатын шеңбер салып, оның центрі арқылы қиюшы жүргіземіз (55-сурет).
Осы қиюшының шеңбер сыртындағы бөлігіне
шеңбермен қиылысу нүктесінен бастап в – ға
тең кесіндіні белгілейміз де, табылған нүкте
(кесіндінің екінші ұшы) арқылы шеңберге АТ
жанамасын жүргіземіз (Т – жанасу нүктесі).
Сонда х = АТ.
І

ІІ әдіс: (а в жағдайы үшін). Диаметрі MN = a шеңбер салып, MN кесінді-сіне МК = в кесіндісін белгілейміз (56-сурет).
Содан соң К нүктесі арқылы MN–ға перпен -
дикуляр тұрғызып, оның шеңбермен қимасын
Х деп белгілесек, МХ ізделінді кесінді болады,
яғни х = МХ.
ІХ. х =
Х. х =
Кейбір есептерде кесінді күрделі формулалармен беріледі. Оларды шешу үшін қарапайым түрге келтіру керек. Мысалдар қарастырайық:
1) х = а
2) х = a
түрінде жазып, V және VІІІ салуларды орындаймыз.
3) х =
4) х =
5) х =
6) х =
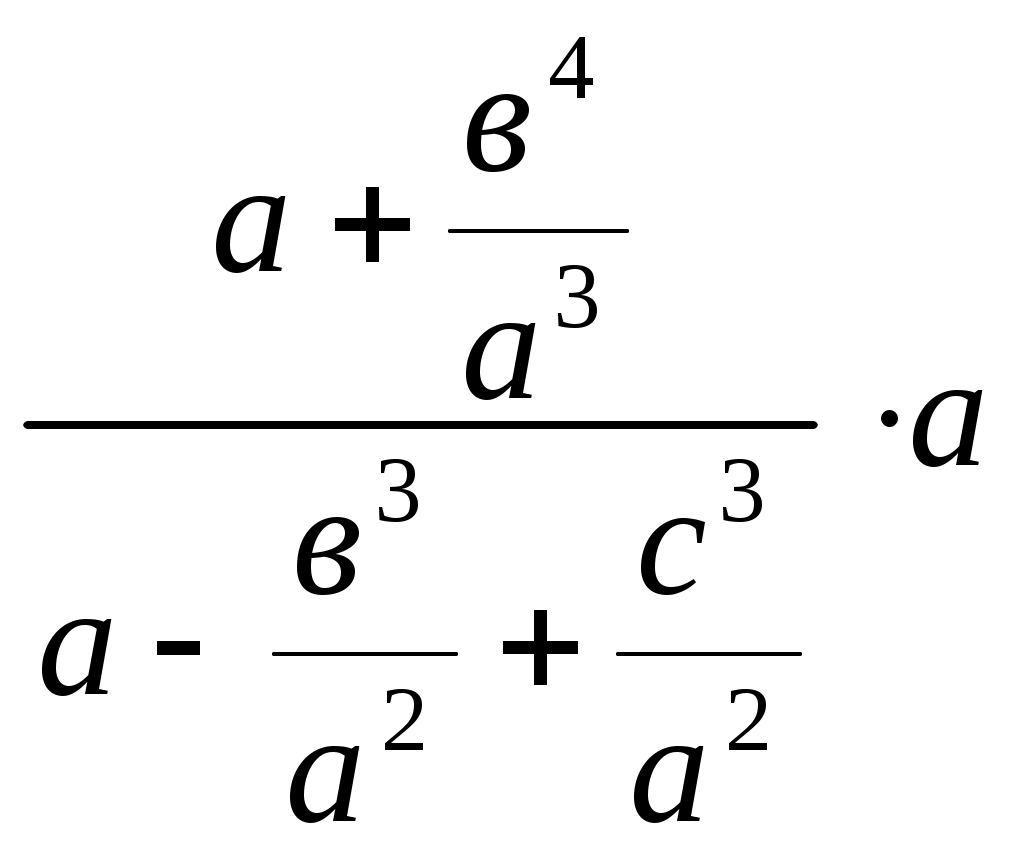 түрінде жазып, у, z, х кесінділерін ретімен саламыз: y = a+
түрінде жазып, у, z, х кесінділерін ретімен саламыз: y = a+ z =
7) х =
х =
, x =
3.2. Квадрат теңдеудің түбірлерін тұрғызу
Айталық p және q кесінділері берілген. Ұзындығы х2 рх q2 = 0 квадрат теңдеуінің нақты түбірлеріне тең болатын кесіндіні есептемей – ақ салатындай ереже жасауға болады. Мұндағы х2 рх q2 = 0 теңдігі тіктөртбұрыш (рх) пен екі квадраттың (х2 & q2) аудандарының байланысы түрінде жазылғандықтан, босмүшені q емес, q2 түрінде жазамыз.
Көрсетілген есепті шешу үшін Виет формуласын немесе квадрат теңдеудің түбірлерінің формуласын қолдануға болады. Екі әдісті де қарастырайық:
І әдіс:
1) х2 - рх + q2 = 0 теңдеуі үшін
х1 =
Гипотенузасы ОА =
2) х2 - рх - q2 = 0 теңдеуі үшін
х1 =
Бұл жағдайда салу жоспары төмендегіше болады:
1. ОС =
2. (О,
3. ОА түзуі
4. ОА = D1 және D2 нүктелері
х1 = AD1, x2 = AD2 – ізделінді кесінділер.
3) х2 + рх q2 = 0 теңдеуін шешу үшін х = -у деп алып, жоғарда көрсетілген салуларды қолданамыз.
ІІ әдіс: ( Виет формуласы арқылы шешу)
1) Талдау: х2 - рх + q2 = 0 теңдеуінің түбірлері Виет формуласы бойынша мынандай байланыста болады:
х1 + х2 = р, х1 х2 = q2.
Сонда квадрат теңдеудің түбірлерін тұрғызу қосындысы және геометриялық ортасы берілген екі кесіндіні салу есебіне келеді.
Салу: 1. Диаметрі АВ = р болатын шеңбері (58-сурет)
2. АВ диаметрінен q қашықтықтағы DЕ параллель түзуі
3. DЕ = Ғ нүктесі
4. ҒС АВ және С АВ түзуі
х1 = AС, x2 = ВС – ізделінді кесінділер.
Зерттеу: Салу жоспарының үшінші қадамындағы DЕ түзуі (О,
болады. Сондықтан х1 = х2, яғни есептің жалғыз шешімі болады. Егер q
2) х2 - рх - q2 = 0 теңдеуінің түбірлері х1 + х2 = р, х1 х2 = - q2 шарттары арқылы байланысқан. Бұдан бір түбірі оң (айталық х1), ал екіншісі теріс (яғни х2) екені көрініп тұр. Олай болса, х1 = х1, х2 =-х2. Сондықтан х1 -х2= p, x1 х2= q2. Сонымен бұл айырмасы және геометриялық ортасы берілген екі кесіндіні салу есебіне келеді. Салу жоспары былайша болады: (59-сурет)
1) (О,
2) кез – келген Т нүктесінен t жанамасы
3) ТА = q болатындай А t нүктесі
4) ОА түзуі
5) ОА = D1, D2 (AD1 AD2) нүктелері
AD1, AD2 – ізделінді кесінділер, яғни х1 = AD1, x2 = AD2.

3.3. Тригонометриялық функциялар арқылы өрнектелген кесіндіні салу

Берілген бұрыштың тригонометриялық функциясына байланысты кесінділерді сызғыш пен циркульды пайдаланып салуға болады. Мысалдар қарастырайық:
1-мысал: с кесіндісі және сүйір бұрышы
берілген. х = c cos, y = c sin формулала -
рымен берілген х,у кесінділерін салу керек.
Ол үшін