Файл: 1 Классификация и физический механизм работы вч и свч генераторов.docx

- определение с помощью ВАХ электронного прибора формы тока на его выходе при подаче на вход синусоидального сигнала;

- разложение в ряд Фурье согласно (4.5) полученной несинусоидальной зависимости для тока эквивалентного генератора электронного прибора (см. рис. 2.1,б);

-определение напряжения на выходе электронного прибора; определение выходной мощности 1-й гармоники поступающей в нагрузку;

- определение потребляемой мощности от источника постоянного тока и КПД генератора;

- анализ входной цепи ВЧ генератора, определение мощности входного сигнала , и коэффициента усиления генератора по мощности ,

- выбор схемы и расчет выходной и входной согласующих электрических цепей ВЧ генератора (см. рис. 2.1,а).

2.2. Баланс мощностей в ВЧ генераторе

Поскольку в ВЧ генераторе происходят процессы преобразования энергии разных источников, то важно составить баланс мощностей для выходной и входной цепей всего устройства.

В выходной цепи происходит преобразование энергии источника постоянного тока мощностью в энергию высокочастотных колебаний мощностью . Поэтому для нее баланс мощностей имеет вид

, (2.1)

где - мощность, рассеиваемая в виде тепла в электронном приборе (в лампе - на аноде, в биполярном транзисторе - на коллекторе, в полевом - на стоке).

---

Мощность рассеивания можно определить как разность или с помощью определенного интеграла:

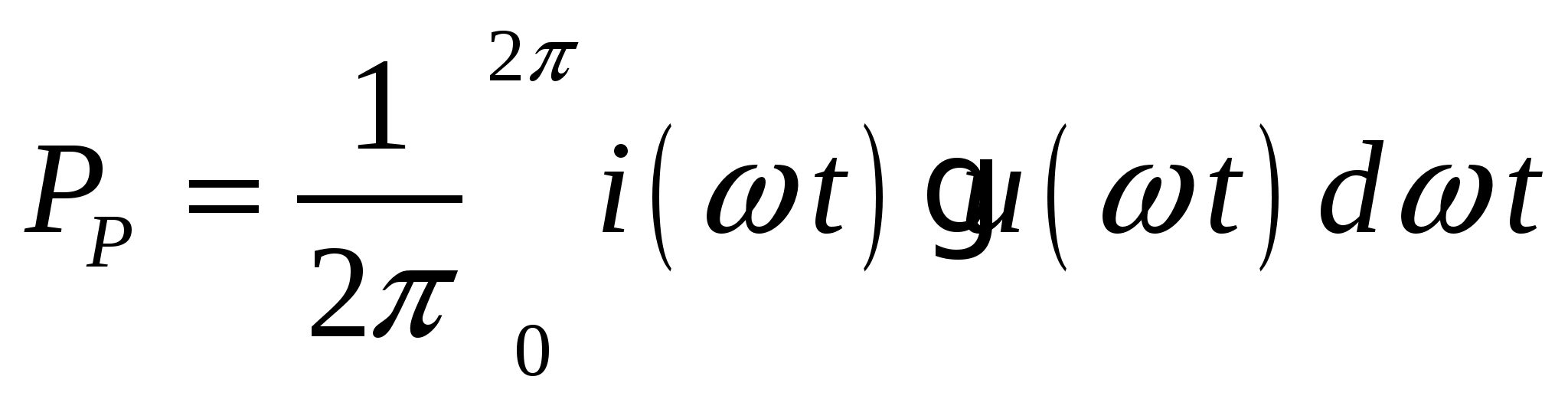, (2.2)

где , - ток и напряжение на выходе электронного прибора. Во входной цепи первичным источником является высокочастотный генератор с ЭДС (см. рис. 2.1,а), отдающий ВЧ генератору мощность . Поэтому во входной цепи баланс мощностей имеет вид

, (2.3)

где - мощность, передаваемая источнику постоянного тока во входной цепи, если таковой имеется; - мощность, рассеиваемая в виде тепла в электронном приборе (в лампе - на управляющей сетке, в биполярном транзисторе - в базе, в полевом - на затворе).

Суммарная мощность тепла, рассеиваемая в электронном приборе, согласно (2.1) и (2.3) запишется в виде . Значение не должно превышать максимально допустимую мощность рассеивания электронного прибора, указываемую в его паспорте.

2.3. Динамические характеристики ВЧ генератора и максимально отдаваемая им мощность

Л
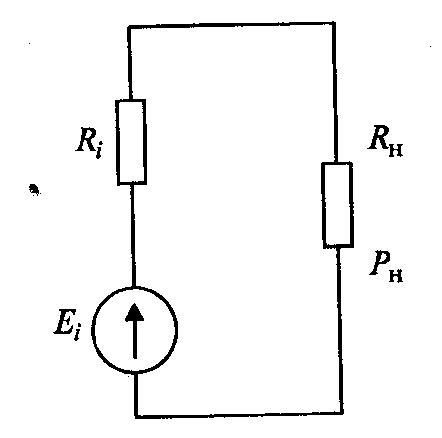юбой генератор отдает максимальную мощность в нагрузку при выполнении определенного условия. Из курса электротехники известно, что генератор с ЭДС и внутренним сопротивлением

---

; при и отдает в нагрузку максимальную мощность, равную , при (рис. 2.3). Мощность называется номинальной мощностью генератора.

Рис. 2.3. Определение номинальной мощности генератора.

В ВЧ генераторах оба параметра ( и ), зависящие от многих факторов, не являются постоянными величинами, и поэтому здесь условие получения максимальной мощности, передаваемой генератором в нагрузку, усложняется и вытекает из понятия «динамическая характеристика генератора по 1-й гармонике сигнала». Пусть в результате эксперимента или расчета найдены зависимости для функций напряжения и тока , на выходе электронного прибора. Пример графиков таких функций приведен на рис. 4.4,а,б. Из двух данных зависимостей, исключив время t, можно получить третью , называемую динамической характеристикой ВЧ генератора для мгновенных значений тока и напряжения (рис. 4.4,в).




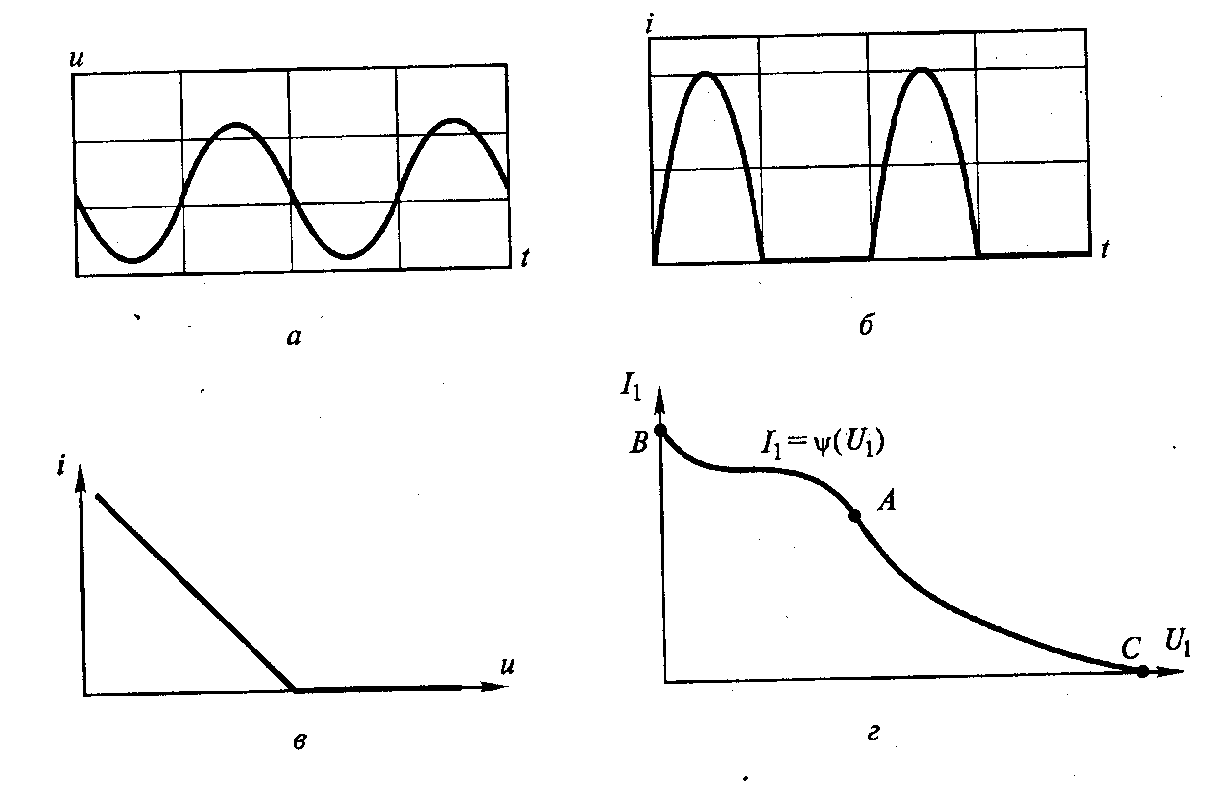
Рис. 2.4. Динамическая характеристика ВЧ генератора для

мгновенных значений тока и напряжения

Разложив в ряд Фурье семейство функций и

---

, определим первые гармоники тока и напряжения . Зависимость называется динамической характеристикой по 1-й гармонике сигнала. Пример такой характеристики приведен на рис. 4.5,г. С ее помощью определим условия передачи максимальной мощности от генератора в нагрузку. Функция является нелинейной, зависящей от частоты и мощности входного сигнала и напряжения питания. Зафиксируем данные параметры и запишем для мощности, передаваемой генератором в нагрузку:

, (2.4)

где - динамическая характеристика ВЧ генератора по 1-й гармонике сигнала (см. рис. 2.5, г); - фазовый угол между векторами и .

Найдем частную производную функции (2.4) и приравняем ее к нулю для определения экстремума функции:

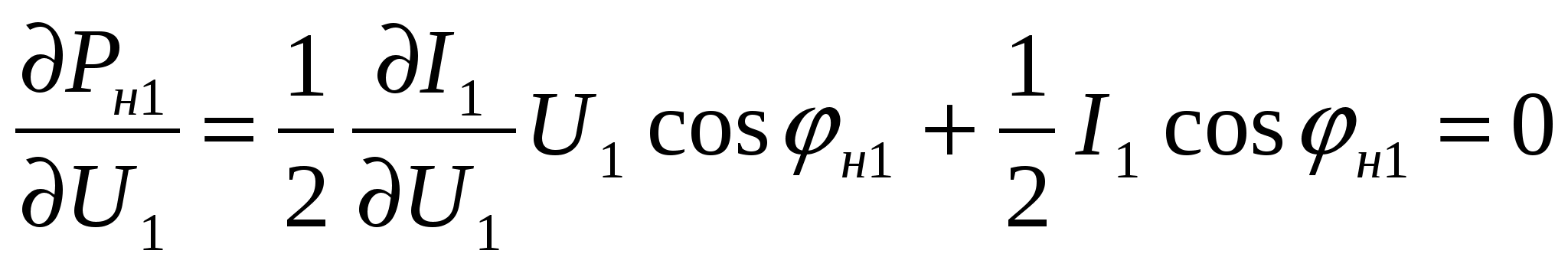, (2.5)

Из (4.5) при получим

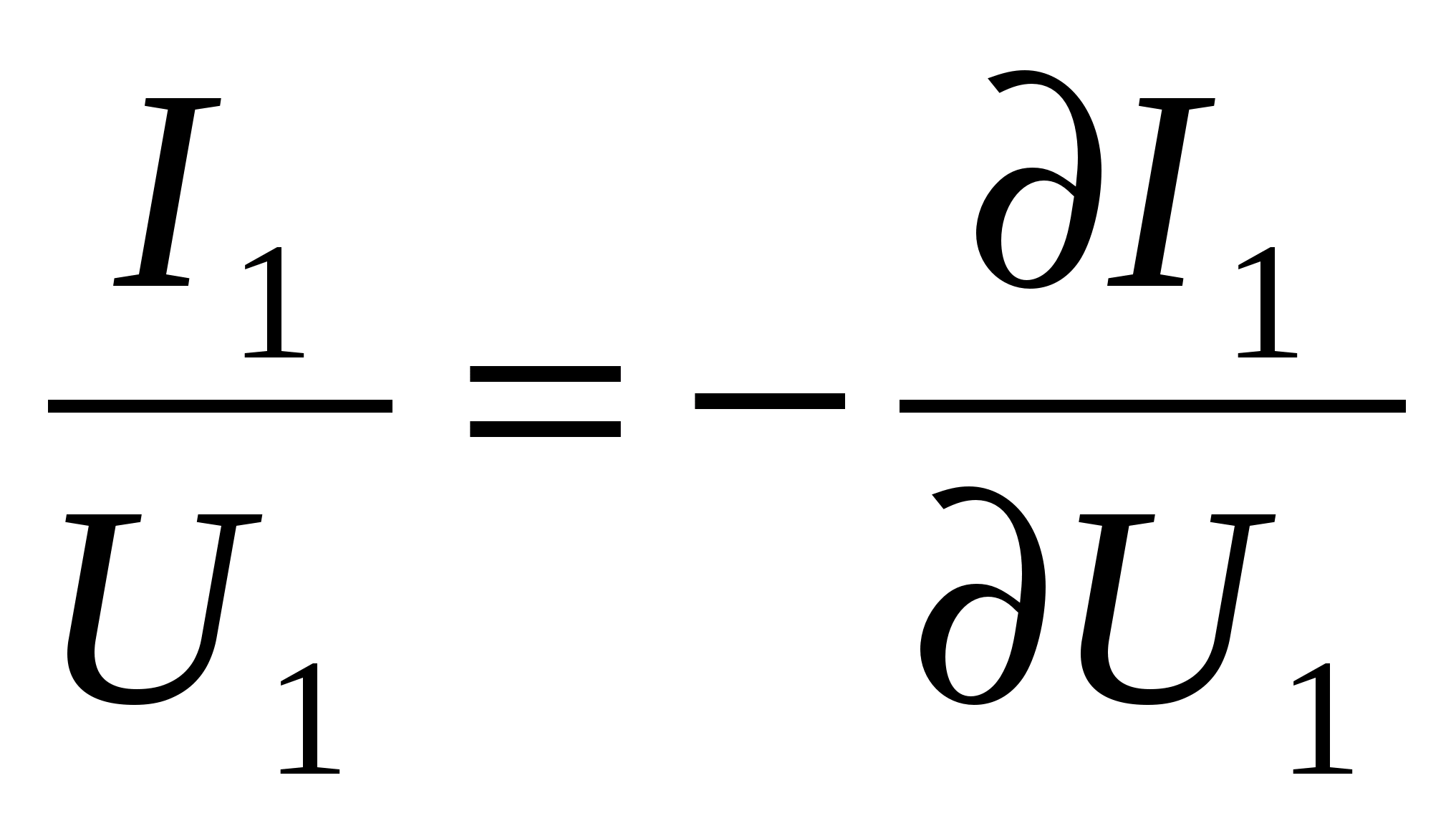. (2.6)

На графике функции (см. рис. 2.5,г ) условию (2.6) передачи максимальной мощности от генератора в нагрузку соответствует точка А, режиму короткого замыкания - точка В, холостого хода - точка С. Раскроем физическое содержание выражения (2.6). Под отношением

---

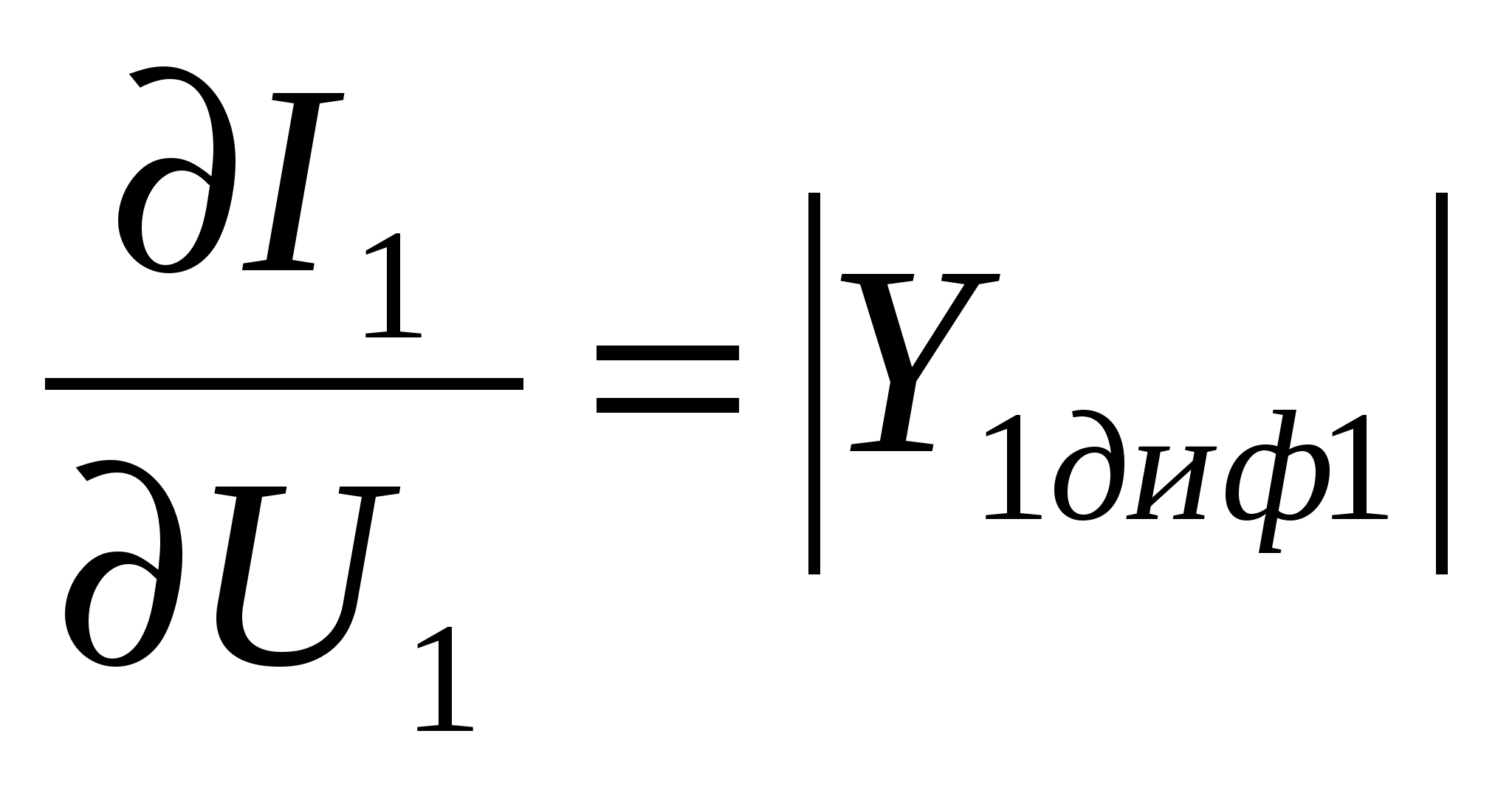
следует понимать модуль внутренней дифференциальной проводимости по 1-й гармонике сигнала эквивалентного генератора. Ее равенство проводимости нагрузки и есть условие передачи максимальной мощности (4.6), которое можно представить в виде

,

где - проводимость нагрузки, подключенной к выходу электронного прибора, на частоте 1-й гармоники сигнала.

Точку А на динамической характеристике (см. рис. 2.4,г) можно найти графическим путем как точку пересечения двух графиков согласно (2.6). Для этого необходимо в n-точках динамической характеристики определить значения ее координат и и производную как тангенс угла касательной в этой точке. Далее согласно (4.6) построим два графика:

.

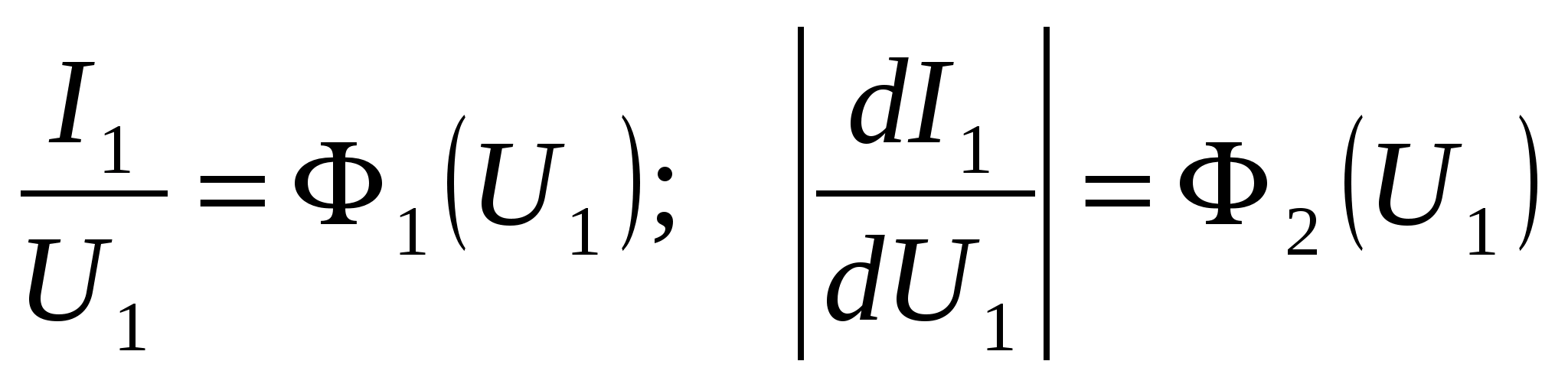Точка пересечения данных графиков определяет условия получения максимальной мощности отдаваемой ВЧ генератором в нагрузку. Чтобы убедиться в этом, следует построить график зависимости . Пример таких построений приведен на рис. 2.5. На рисунке показаны зависимости (см. рис. 2.5,а), и (см. рис. 2.5,б), (см. рис. 2.5,в).



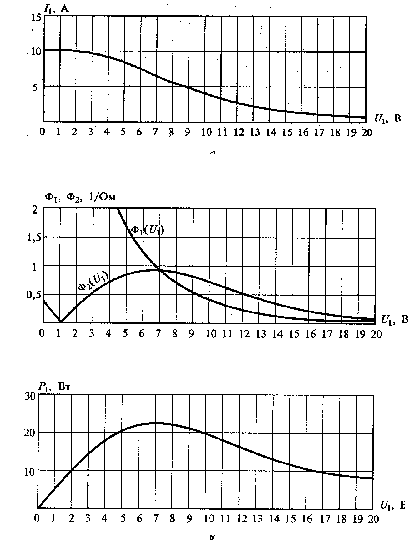
Рис. 2.5. Условие получения максимальной мощности, отдаваемой генератором по 1-й гармонике сигнала.

---