Файл: Отчет по практической работе 1 Вариант 25 по дисциплине Метрология, стандартизация и сертификация.docx
Добавлен: 10.01.2024
Просмотров: 74
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Гипотеза H0— распределение результатов измерений соответствует нормальному виду;
Гипотеза H1 — распределение результатов измерений не соответствует нормальному виду.
-
Выбор вида статистической проверки гипотезы.
Для проверки гипотезы о том, что результаты наблюдений принадлежат нормальному закону распределения, будет использован критерий А.
-
Определение уровня значимости.
Уровень значимости q согласно заданию равен 0,01 (1%).
-
Вычисление критического значения выбранного статистического критерия на основе исходных данных.
Согласно критерию А критическое значение определяется по формуле:
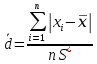
Далее, для удобства расчетов следует составить таблицу 3.
Результаты промежуточных расчетов критерия А
 |  |
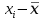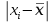| 1,94008  |  |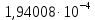
| 7,87776 | 7,87776 |
| -9,08392 | 9,08392 |
| 6,67898  |  |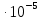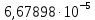
| 3,12762 | 3,12762 |
| -9,52410 | 9,52410 |
| 5,51962 | 5,51962 |
| 5,57525 | 5,57525 |
| -1,59818 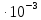 | 1,59818 |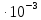
| 3,15664 | 3,15664 |
| -6,51778 | 6,51778 |
| -1,81359 |  |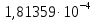
| 7,96725 | 7,96725 |
| -1,87889 |  |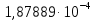
| 6,19526 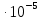| 6,19526 |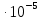
| 5,80985 | 5,80985 |
| -1,88857 | 1,88857 |
| 1,26287 | 1,26287 |
| 5,56557 | 5,56557 |
| -2,40131 | 2,40131 |
| ∑ | 9,81799 |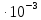
| | |
Тогда:
-
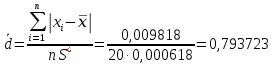
Нахождение в таблицах квантиля распределения.
Согласно таблице B.1 приложения В при уровне значимости q и объеме выборки n квантили распределения
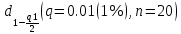и 
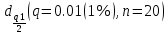равны: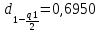
-
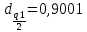
Проверка, выполняется ли указанное в выбранном критерии условие. Согласно критерию А, распределение результатов наблюдений соответствует нормальному виду, если выполняется неравенство:
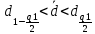
где:
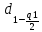И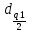 
квантили распределения, получаемые из таблицы B.1 приложения В.
При подстановке значений данное условие примет вид:
0,6950 < 0,793723 < 0,9001.
-
Формулировка вывода.
Видно, что условие
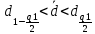выполняется, следовательно принимается нулевая гипотеза и отвергается альтернативная гипотеза.Вывод: условие критерия А выполняется, следовательно, отвергается альтернативная гипотеза (H1) и принимается нулевая гипотеза (H0), согласно которой распределение результатов измерений соответствует нормальному.
Критерий Б
-
Формирование исходных данных.
Исходные данные для исследования представлены в таблице 1.
-
Формулировка нулевой (H0) и альтернативной (H1) гипотез.
Гипотеза
H0— распределение результатов измерений соответствует нормальному;
Гипотеза H1 — распределение результатов измерений не соответствует нормальному.
-
Выбор вида статистической проверки гипотезы.
Для проверки гипотезы о том, что результаты наблюдений принадлежат нормальному закону распределения, будет использован
-
Определение уровня значимости.
Уровень значимости q согласно заданию равен 0,01 (1%).
-
Вычисление фактического значения выбранного статистического критерия на основе исходных данных.
Поскольку в данном критерии расчеты и проверка связаны друг с другом, все вычисления сведены в один этап.
-
Нахождение в таблицах квантиля распределения.
Согласно таблице B.2 приложения В для числа измерений n = 20, значение параметра m равно 1, уровень доверительной вероятности Рдля уровня значимости q = 0,01 (1%) составляет 0,99.
Тогда согласно таблице В.3 приложения В значение квантиля
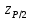составляет:
.-
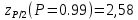Проверка, выполняется ли указанное в выбранном критерии условие.
Согласно критерию Б, распределение результатов наблюдений соответствует нормальному, если не более m разностей
превысили значение 
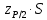т.е.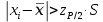
где S
—среднее квадратическое отклонение;
— верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности P/2.В данном случае:
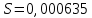
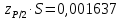
Далее, для удобства расчетов следует составить таблицу 4.
Результаты промежуточных расчетов критерия Б
| | |  |
 | < | 0,001637 |
| 7,87776  | < | |
| 9,08392 | < | |
 | < | |
| 3,12762 | < | |
| 9,52410 | < | |
| 5,51962 | < | |
| 5,57525 | < | |
| 1,59818  | < | |
| 3,15664 | < | |
| 6,51778 | < | |
 | < | |
| 7,96725 | < | |
 | < | |
| 6,19526  | < | |
| 5,80985 | < | |
| 1,88857 | < | |
| 1,26287 | < | |
| 5,56557 | < | |
| 2,40131 | < |
Как видно из таблицы 4 ни одна разность вида
не превысила значение , следовательно, критическая статистика — m* = 0.-
Формулировка вывода.
Вывод: установлено, что ни одна из разностей
не превысила значение , следовательно, отвергается альтернативная гипотеза (H1) и принимается нулевая гипотеза (H0), согласно которой распределение результатов измерений соответствует нормальному.Поскольку оба критерия установили, что распределение результатов наблюдений группы соответствует нормальному виду, то формируется соответствующий вывод: вид закона распределения результатов наблюдений выборки соответствует нормальному