Файл: Отчет по практической работе 1 Вариант 25 по дисциплине Метрология, стандартизация и сертификация.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 77

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Вычисление среднего арифметического исправленных результатов наблюдений

Вычисление доверительных границ случайной погрешности



Исключение известных систематических погрешностей из результатов измерений путем введения поправок
Исследование проводится согласно приведенному ранее порядку.

  1. Формирование исходных данных.

Исходные данные для исследования представлены в таблице 1.

  1. Формулировка нулевой (H0) и альтернативной (H1) гипотез.

Гипотеза H0— группа результатов измерений содержит постоянно возрастающую или постоянно убывающую систематическую погрешность;

Гипотеза H1 — группа результатов измерений не содержит постоянно возрастающую или постоянно убывающую систематическую погрешность.

  1. Выбор вида статистической проверки гипотезы.

Для исследования результатов измерений на наличие систематических погрешностей будет использован критерий Аббе.

  1. Определение уровня значимости.

Уровень значимости q согласно заданию равен 0,01 (1%).

  1. Вычисление критического значения выбранного статистического критерия на основе исходных данных.

Согласно критерию Аббе критическое значение определяется по формуле:



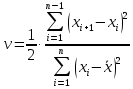
где xi– i-й результат измерений группы;

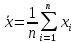– среднее арифметическое группы результатов измерений.

n – число измерений в группе

Для начала следует определить среднее арифметическое группы результатов измерений:



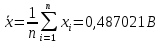
Результаты промежуточных расчетов сведены в таблицу 2.






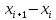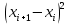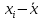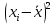5,93767 ∙10-4
3,52560 ∙10-7
1,94008 ∙10-4
3,76392∙10-8

-1,69617 ∙10-3
2,87698 ∙10-6
7,87776 ∙10-4
6,20591∙10-7

9,75181 ∙10-4
9,50979 ∙10-7
-9,08392 ∙10-4
8,25175∙10-7

2,45972 ∙10-4
6,05023 ∙10-8
6,67898 ∙10-5
4,46087∙10-9

-1,26571 ∙10-3
1,60066 ∙10-6
3,12762 ∙10-4
9,78200∙10-8

1,50437 ∙10-3
2,26314 ∙10-6
-9,52410 ∙10-4
9,07085∙10-7

5,56279 ∙10-6
3,09446 ∙10-11
5,51962 ∙10-4
3,04662∙10-7

-2,15570 ∙10-3
4,64705 ∙10-6
5,57525 ∙10-4
3,10834∙10-7

1,91384 ∙10-3
3,66279 ∙10-6
-1,59818 ∙10-3
2,55417∙10-6

-9,67442 ∙10-4
9,35944 ∙10-7
3,15664 ∙10-4
9,96439∙10-8

4,70419 ∙10-4
2,21294 ∙10-7
-6,51778 ∙10-4
4,24814∙10-7

9,78084 ∙10-4
9,56648 ∙10-7
-1,81359 ∙10-4
3,28911∙10-8

-9,84614 ∙10-4
9,69465 ∙10-7
7,96725 ∙10-4
6,34770∙10-7

2,49842 ∙10-4
6,24210 ∙10-7
-1,87889 ∙10-4
3,53024∙10-8

5,19033 ∙10-4
2,24210 ∙10-7
6,19526 ∙10-5
3,83812∙10-9

-7,69842 ∙10-4
6,92656 ∙10-7
5,80985 ∙10-4
3,37544∙10-7

3,15144 ∙10-4
1,93159 ∙10-7
-1,88857 ∙10-4
3,56669∙10-8

4,30270 ∙10-4
1,85132 ∙10-7
1,26287 ∙10-4
1,59485∙10-8

-7,96688 ∙10-4
6,34712∙10-7
5,56557 ∙10-4
3,09756∙10-7







-2,40131 ∙10-4
5,76630∙10-8

∑
2,1342∙10-5
∑
7,65028∙10-6

После этого, используя данные таблицы 2, определяется критическое значение:



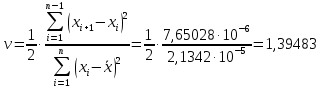
  1. Нахождение в таблицах квантиля распределения.

Согласно таблице Б.1 приложения Б при уровне значимости q = 0,01 и объеме выборки п = 20 квантиль vt(q, п) будет равен:



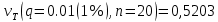
  1. Проверка, выполняется ли указанное в выбранном критерии условие.

Согласно критерию Аббе, группа результатов измерений содержит постоянно возрастающую или постоянно убывающую систематическую по грешность, если выполняется неравенство:



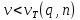
где 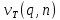— квантиль распределения, соответствующий уровню значимости q и числу измерений n в группе.

При подстановке значений данное неравенство принимает вид:

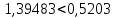
  1. Формулировка вывода.

Видно, что условие 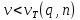не выполняется, следовательно, отвергается нулевая и принимается альтернативная гипотеза.

Вывод: условие критерия Аббе не выполняется, следовательно, отвергается нулевая гипотеза (H0) и принимается альтернативная гипотеза (H1), согласно которой группа результатов измерений не содержит постоянно возрастающую или постоянно убывающую систематическую погрешность.

Поскольку исследование показало, что в исходных данных отсутствует систематическая погрешность, нет необходимости вводить поправки.


Отсутствие грубой погрешности (промахов) и монотонной систематической погрешности в выборке результатов наблюдений подтверждает точность представленных данных.

Вычисление среднего арифметического исправленных результатов наблюдений


За результат измерений (оценку измеряемой величины) принимают среднее арифметическое результатов наблюдения:

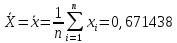B



Вычисление среднего квадратического отклонения


Для расчета среднего квадратического отклонения результатов измерений и смещенной оценки среднего квадратического отклонения можно воспользоваться данными из таблицы 2. Тогда:




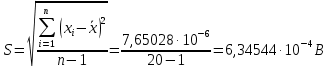
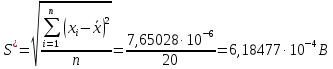
Среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины) можно найти из среднего квадратического отклонения результатов измерений: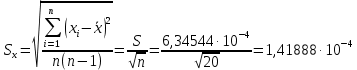






Проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению




Согласно ГОСТ 8.736-2011 при числе результатов измерений 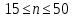нормальность их распределения проверяют с помощью составного критерия. Исследование будет проводиться в 2 этапа: проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению по критерию А; проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению по критерию Б.

Критерий А

  1. Формирование исходных данных.

Исходные данные для исследования представлены в таблице 1.

  1. Формулировка нулевой (H0) и альтернативной (H1) гипотез.

Смотрите также файлы