Файл: В юридической деятельности.docx

Поскольку случайная величина I может принимать множество значений в зависимости от того или иного исхода события, то для ее числовой характеристики (количества информации I в произвольном сообщении об исходе случайного события) принимается ее математическое ожидание или среднее значение:

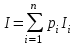(2)

подставляя формулу (1) в формулу (2) получим:

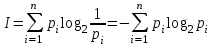(3)

Данная формула была предложена К. Шенноном для определения количества информации в сообщении об исходе случайного события.

Для определения количества информации, содержащемся в сообщении об исходе случайного события в случае, когда все исходы равновероятны, т.е. р₁= р₂=…= р_n формула (3) принимает вид:

I=log₂ n (4)

Эта формула была выведена в 1928 г. американским инженером Р. Хартли и носит его имя.

В качестве единицы количества информации, подсчитываемой по формуле (4), принят 1 бит. Бит – минимально возможное количество информации содержится в сообщении об исходе случайного события с двумя равновероятными исходами. Так, полагая в формуле (4) n=2 и р₁=р₂=0,5 получим:

I=log₂ 2=1 (бит).

Проиллюстрируем это на следующих примерах.

Бросание одной монеты. До момента бросания монеты имеется неопределенность исхода данного события, смысл которой заключается в том, что потенциально возможны два варианта исходов бросания, т.е. n=2 (табл. 2):

Таблица 2

Вариант	Исход бросания	Код сообщения
1	«орел»	1
2	«решка»	0

Закодированное информационное сообщение представляет собой последовательность из одного двоичного символа (табл. 2). В этом случае любое из этих двух сообщений (0 или 1) уменьшает неопределенность ровно в два раза. Применяя для данного примера формулу Хартли, получим:

I=log₂ 2=1 (бит).

Таким образом, сообщение об исходе бросания одной монеты несет в себе количество информации равное 1 бит. Иными словами, 1 бит есть та минимальная порция информации, которая уменьшает исходную неопределенность в два раза в линейном масштабе.

Бросание одновременно трех монет

---

. До момента бросания монет имеется неопределенность исхода данного события, смысл которой заключается в том, что потенциально возможны восемь вариантов исходов бросания, т.е. n=8 (табл. 3).

В этом случае закодированное информационное сообщение представляет собой последовательность из трех двоичных символов (табл. 3). Применяя для рассматриваемого примера формулу (4), получим:

I=log₂ 8=3 (бит)

Таблица 3

Вариант	1-ая монета	2-ая монета	3-я монета	Код сообщения
1	«орел»	«орел»	«орел»	111
2	«решка»	«решка»	«решка»	000
3	«орел»	«решка»	«решка»	100
4	«орел»	«орел»	«решка»	110
5	«орел»	«решка»	«орел»	101
6	«решка»	«орел»	«орел»	011
7	«решка»	«решка»	«орел»	001
8	«решка»	«орел»	«решка»	010

Таким образом, любое сообщение об исходе бросания трех монет несет в себе количество информации, равное трем битам, т.е. уменьшает неопределенность об исходе данного события ровно в восемь раз (в линейном масштабе).

Интересно, что согласно классической теории информации, сообщение об исходе бросания одновременно трех монет несет в себе в три раза больше информации (в логарифмическом масштабе), чем сообщение об исходе бросания одной монеты (3 бита и 1 бит).

Следует отметить, что в компьютерной технике при передаче сообщений по линиям связи в качестве случайных событий выступают передаваемые последовательности нулей и единиц, представляющие собой закодированные (т.е. представленные в цифровой форме) текстовые, числовые, графические, звуковые и другие сообщения. Данные последовательности имеют различную (случайную) длину и различный (случайный) характер чередования нулей и единиц.

---

Если под исходом случайного события понимать конкретный вид последовательности нулей и единиц в передаваемом сообщении, то данные исходы не являются равновероятными и, следовательно, для определения количества содержащейся в них информации нельзя использовать формулу Хартли. Как следствие, в этом случае нельзя использовать в качестве единицы информации 1 бит.

Таким образом, единица измерения 1 бит малопригодна на практике для определения количества информации, содержащейся в сообщении в классическом понимании этого термина (мера уменьшения неопределенности). Гораздо чаще, если не всегда, в компьютерной технике бит выступает в качестве элементарной единицы количества или объема хранимой (или передаваемой) информации безотносительно к ее содержательному смыслу.

Количество информации в 1 бит является слишком малой величиной, поэтому наряду с единицей измерения информации 1 бит, используется более крупные единицы:

1байт=2³ бит=8 бит.

1 килобайт (1 Кбайт) = 2¹⁰ байт = 1024 байт,

1 мегабайт (1 Мбайт) = 2¹⁰ Кбайт = 1024 Кбайт,

1 гигабайт (1 Гбайт) = 2¹⁰ Мбайт=1024 Мбайт,

1 терабайт (1 Тбайт) = 2¹⁰ Гбайт (1024 Гбайт),

1 петабайт (1 Пбайт) = 2¹⁰ Тбайт (1024 Тбайт).

В компьютерной и телекоммуникационной технике в битах, байтах, килобайтах, мегабайтах и т.д. измеряется также потенциальная информационнаяемкость оперативной памяти и внешних запоминающих устройств, предназначенных для хранения данных (жесткие диски, дискеты, CD-ROM и т.д.).

3. Понятие энтропии

В 1948 году, исследуя проблему рациональной передачи информации через зашумленный коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных шифров.

Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.

Энтропия (от греч. поворот, превращение) – понятие, впервые возникшее в термодинамике как мера необратимого рассеяния энергии; широко применяется в других областях: в статистической механике – как мера вероятности осуществления состояния системы; в теории информации – как мера неопределенности сообщений; в теории вероятностей – как мера неопределенности опыта, испытания с различными исходами; ее альтернативные трактовки имеют глубокую внутреннюю связь: например из вероятностных представлений об информации можно вывести все важнейшие положения статистической механики.

---

В термодинамике понятие энтропии было введено немецким физиком Р. Клаузисом (1865), когда он показал, что процесс превращения теплоты в работу подчиняется закономерности – второму началу термодинамики, которое формулируется строго математически, если ввести функцию состояния системы – энтропию. Клаузис также показал важность понятия энтропии для анализа необратимых (неравновесных) процессов, если отклонения от термодинамики равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но еще макроскопических объемах. В целом энтропия неравновесной системы равна сумме энтропий ее частей, находящихся в локальном равновесии.

Статистическая механика связывает энтропию с вероятностью осуществления макроскопического состояния системы знаменитым соотношением Больцмана «энтропия – вероятность»

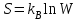(5)

где W – термодинамическая вероятность осуществления данного состояния (число способов реализации состояния), а k_B – постоянная Больцмана.

В отличие от термодинамики статистическая механика рассматривает специальный класс процессов – флуктуации, при которых система переходит из более вероятных состояний в менее вероятные и вследствие этого ее энтропия уменьшается. Наличие флуктуаций показывает, что закон возрастания энтропии выполняется только статистически: в среднем для большого промежутка времени.

Понятие энтропии распределения в теории вероятностей математически совпадает с понятием информационной энтропии. Из вероятностной трактовки энтропии выводятся основные распределения статистической механики: каноническое распределение Гиббса, которое соответствует максимальному значению информационной энтропии при заданной средней энергии; и большое каноническое распределение Гиббса – при заданной средней энергии и количестве частиц в системе.

Энтропия в теории информации – мера хаотичности информации, неопределенность появления какого-либо символа первичного алфавита. При отсутствии информационных потерь энтропия численно равна количеству информации на символ передаваемого сообщения.

Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу.

Энтропия независимых случайных событий x

---

с n возможными состояниями (от 1 до n) рассчитывается по формуле:

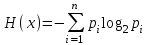(6)

Эта величина также называется средней энтропией сообщения. Величина 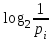называется частной энтропией, характеризующей только i-e состояние.

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы. Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

Шеннон вывел это определение энтропии из следующих предположений:

мера должна быть непрерывной; т.е. изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение энтропии;

в случае, когда все варианты равновероятны, увеличение количества вариантов должно всегда увеличивать полную энтропию;

должна существовать возможность сделать выбор в два шага, в которых энтропия конечного результата должна будет являться суммой энтропий промежуточных результатов.

Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме:

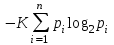(7)

где K – константа (в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии ( 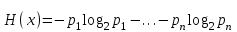), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надежной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидания «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка – имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т.д.

---