Файл: В юридической деятельности.docx

Фрактальная графика

Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видов компьютерной графики. Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от так называемых «родителей» геометрических свойств объектов-наследников.

Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.

Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале.

В центре фрактальной фигуры находится ее простейший элемент – равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной ( 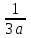) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной ( 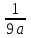) от стороны исходного треугольника.

Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом, можно описать и такой графический элемент, как прямую.

Изменяя и комбинирую окраску фрактальных фигур можно моделировать образы живой и неживой природы, а также, составлять из полученных фигур «фрактальную композицию». Фрактальная графика, также как векторная и трехмерная, является вычисляемой. Ее главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется.

---

Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.

Итак, базовым понятием для фрактальной компьютерной графики являются «фрактальный треугольник». Затем следуют «фрактальная фигура», «фрактальный объект»; «фрактальная прямая»; «фрактальная композиция»; «объект-родитель» и «объект наследник».

Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать такие композиционные приемы как, горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сравнить фрактальное изображение можно со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную структуру. Это свойство фрактального объекта может быть удачно использовано при составлении декоративной композиции или для создания орнамента. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу.

С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной графике найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Геометрические фракталы на экране компьютера – это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.

Создатель фракталов – это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Задается форма рисунка математической формулой, исследуя сходимость процесса, варьируя его параметры, выбирается вид изображения и палитра цветов, то есть создается рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов от прочих графических программ.

3. Цветовые модели и форматы графических изображений

Окружающий нас мир полон всевозможных цветов и цветовых оттенков. С физической точки зрения цвет – набор определённых длин волн, отражённых от предмета или пропущенных сквозь прозрачный предмет. С развитием многих отраслей производства, в том числе, полиграфии, компьютерных технологий, появилась необходимость объективных способов описания и обработки цвета. Большинство цветов получаются смешением каких-либо других. Например, сочетание красного и синего даёт пурпурный цвет, синего и зелёного - голубой. Таким образом, путём смешения из небольшого количества простых цветов, можно получить множество сложных (составных). Поэтому для описания цвета вводится понятие

---

цветовой модели – как способа представления большого количества цветов посредством разложения его на простые составляющие.

Модель RGB.

В модели RGB производные цвета получаются в результате сложения или смешения базовых, основных цветов, называемых цветовыми координатами. Координатами служат красный, зеленый и синий цвет. Свое название RGB-модель получила по первым буквам английских наименований цветовых координат. Свойства модели RGB хорошо описывается цветовым кубом (рис. 6). Это фрагмент трехмерного пространства, координатами которого являются красный, зеленый и синий цвет. Каждая точка внутри куба соответствует некоторому цвету и описывается тремя проекциями – цветовыми координатами: содержанием красного, зеленого и синего цвета. Сложение всех основных цветов максимальной яркости дает белый цвет; начальная точка куба означает нулевые значения основных цветов и соответствует черному цвету. Если цветовые координаты смешивать в равных пропорциях, то получится серый цвет разной насыщенности. Точки, отвечающие серому цвету, лежат на диагонали куба. Смешение красного и зеленого дает желтый, красный и синий образуют пурпурный, а зеленый и синий – голубой. Цветовые координаты: красный, зеленый и синий называют первичными или аддитивными цветами. Цвета голубой, пурпурный, желтый, которые получаются в результате попарного смешения первичных цветов, называются вторичными. Поскольку сложение это основная операция синтеза цветов, то модель RGB иногда называют аддитивной. Принцип сложения цветов изображается в виде плоской круговой диаграммы.

По принципу сложения цветов работают многие технические устройства: мониторы, телевизоры, сканеры, цифровые фотоаппараты и др. Если увеличить экран монитора, то можно увидеть регулярную сетку, в узлах которой располагаются красные, зеленые и синие точки - зерна люминофора. Базовые цвета разной интенсивности излучаются при возбуждении пучка электронов. Сложение излучений близко расположенных зерен воспринимается человеческим глазом как цвет в данной точке экрана. Интенсивность первичных цветов измеряется целыми числами в диапазоне от 0 до 255. Ноль означает отсутствие данной цветовой составляющей, число 255 - ее максимальную интенсивность. Первичные цвета могут смешиваться без ограничений и поэтому можно подсчитать общее количество цветов, 256 * 256 * 256=16 777 216, или более 16,7 миллионов цветов. Любой естественный цвет можно разложить на красную, зеленую и синюю составляющие и измерить их интенсивность. Экспериментально и теоретически доказано, что диапазон цветов модели RGB уже, чем множество цветов видимого спектра. Чтобы получить часть спектра, лежащую между синим и зеленым цветами, требуются излучатели с отрицательной интенсивностью красного цвета, которых, конечно же, в природе не существует. Диапазон воспроизводимых цветов модели или устройства называется цветовым охватом. Одним из серьезных недостатков аддитивной модели, является ее узкий цветовой охват. Еще одним недостатком модели следует считать аппаратную зависимость. Цвет, воспроизводимый устройством, зависит от множества внешних факторов, часто не поддающихся учету. Еще один недостаток этой цветовой модели с точки зрения дизайнера или компьютерного художника, в том, что она является не интуитивной.

---

Модели CMY и CMYK.

Модель CMY использует также три основных цвета: Cyan (голубой), Magenta (пурпурный, или малиновый) и Yellow (желтый). Эти цвета описывают отраженный от белой бумаги свет трех основных цветов RGB модели. Поэтому можно описать соотношения между RGB и CMY моделями следующим образом:

               

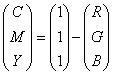
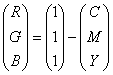
Модель CMY является субтрактивной (основанной на вычитании) цветовой моделью. В CMY-модели описываются цвета на белом носителе, т. е. краситель, нанесенный на белую бумагу, вычитает часть спектра из падающего белого света. Например, на поверхность бумаги нанесли голубой (Cyan) краситель. Теперь красный свет, падающий на бумагу, полностью поглощается. Таким образом, голубой носитель вычитает красный свет из падающего белого. Такая модель наиболее точно описывает цвета при выводе изображения на печать, т. е. в полиграфии.

Так как для воспроизведения черного цвета требуется нанесение трех красителей, использование CMY-модели является не эффективным. Дополнительным фактором является появление нежелательных визуальных эффектов, возникающих за счет того, что при выводе точки три базовые цвета могут ложиться с небольшими отклонениями. Поэтому к базовым трем цветам CMY-модели добавляют черный и получают новую цветовую модель CMYK.

Для перехода из модели CMY в модель CMYK иногда используют следующее соотношение:

K = min(C, M, Y);

C = C – K;

M = M – K;

Y  = Y – K.

Соотношения преобразования RGB в CMY и CMY в CMYK-модель верны лишь в том случае, когда спектральные кривые отражения для базовых цветов не пересекаются (рис.8). Поэтому в общем случае можно сказать, что существуют цвета, описываемые в RGB-модели, но не описываемые в CMYK-модели.
Существует также модель CMYK256, которая используется для более точной передачи оттенков при качественной печати изображений.

Модель HSB

Цветовая модель HSB возникла как попытка преодолеть аппаратную зависимость модели RGB. В модели HSB все цвета определяются тремя координатами оттенком, насыщенностью и яркостью. Название модели образовано по первым буквам английских названий цветовых координат. Цветовым тоном или оттенком называется спектрально-чистый цвет определенной длины волны, например чистый красный или чистый зеленый.

---

Цветовой тон - это объективная характеристика, поскольку ее можно измерить по длинам преобладающих в световом пучке волн. Насыщенность описывает чистоту цвета. Один и тот же тон может быть тусклым или насыщенным. Изменение насыщенности можно представить как разбавление чистого хроматического цвета белым или серым. Чем больше содержание серого, тем более блеклым, менее насыщенным становится цвет. Все цвета естественного происхождения имеют низкую насыщенность, поэтому чистые тона выглядят слишком яркими, ненатуральными. Яркость характеризует интенсивность, энергию цвета. Изменение яркости можно представить как смешение чистого тона и черного цвета. Большое содержание черного делает цвет затененным, неинтенсивным. С уменьшением процента черного освещенность увеличивается. Солнечный луч – пример яркого света, свечение, исходящее от светлячка, имеет очень низкую яркость. Черный цвет имеет нулевую яркость, а белый - максимальную.

Иногда для описания модели HSB используется иная геометрическая аналогия. Пусть цвета видимого спектра располагаются по кругу, как цифры на циферблате часов. Каждому оттенку соответствует точка на окружности. Чтобы указать положение чистого спектрального цвета, достаточно задать угол поворота радиуса-вектора. В большинстве графических программ принято начинать отсчет от красного цвета и располагать основные и дополнительные цвета с приращением 60 градусов (рис. 9). Следует отметить, что направление отсчета и начальная точка – характеристики, которые не имеют принципиального значения и могут быть изменены в программных реализациях данной модели. Величина насыщенности описывается как длина радиуса-вектора. Чем менее насыщенным является цвет, тем ближе к центру окружности располагается представляющая его точка. Центр круга соответствует черному цвету. Обычно насыщенность измеряется в процентах: минимальная насыщенность равна 0, максимальная - 100. Чтобы учесть в модели яркость, надо добавить третью координату. Все цветовое пространство системы HSB можно представить в виде стопки цветовых кругов, каждый из которых соответствует своему значению яркости. Яркость в большинстве графических программ измеряют в процентах в диапазоне от 0 до 100.
Система HSB очень удобна, в ней можно синтезировать новые цвета и получать различные варианты заданного цвета, опираясь на интуицию и изображение цвета. Еще одним несомненным достоинством системы HSB является ее независимость от аппаратуры. По мнению физиков и инженеров-оптиков система HSB является абстрактной. Это значит, что нет таких устройств, которые синтезируют цвет в этой системе. Не существует и прямой процедуры измерения цветового тона и насыщенности. В любом методе ввода информации о цвете сначала измеряются красная, синяя и зеленая составляющие, которые потом пересчитываются в координаты HSB.

---