ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1140
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Дизъюнкция АÚВ (A+B) – сложное высказывание, которое ложно тогда и только тогда, когда оба высказывания А и В одновременно ложны.
Таблица истинности
Логическая операция «Конъюнкция» (логическое «и»). Конъюнкция АÙВ (A&B) – сложное высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно истинны.
Таблица истинности
Логическая операция «Импликация». Импликация высказываний А и В (А®В) – сложное высказывание, которое истинно всегда, кроме случая когда А – истинно, а В – ложно.
Таблица истинности
Логическая операция «Эквивалентность» (двойная импликация).
Эквивалентность высказываний А и В (А«В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны либо ложны и ложно во всех других случаях.
Таблица истинности
Логические элементы. Логические элементы – устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого – «1» и низкого – «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже – на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Рассмотрим логические элементы.
Логический элемент НЕ (инвертор). Простейшим логическим элементом является инвертор, выполняющий функцию отрицания (инверсию). У этого элемента один вход и один выход. На функциональных схемах он обозначается:
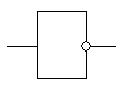
Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
Логический элемент ИЛИ (дизъюнктор). Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:
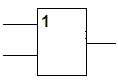
Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1.
Логический элемент И (конъюнктор). Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:
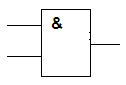
На выходе этого элемента будет сигнал 1 только в том случае, когда на все входы поступает сигнал 1. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Другие логические элементы построены из трех рассмотренных нами базовых элементов и выполняют более сложные логические преобразования информации. Рассмотрим примеры таких элементов.
Логический элемент И-НЕ. Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (И-НЕ). Имеет, как минимум, два входа. На функциональных схемах обозначается:
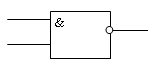
Логический элемент ИЛИ-НЕ. Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (И-НЕ). Имеет, как минимум, два входа. На функциональных схемах обозначается:
Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов – функциональные схемы. Рассмотрим пример.
Задача 1. Записать логическую формулу для следующей функциональной схемы:
1. Инверсия ¬А: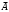
.
2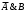
. Логическое умножение значений ¬А и В: 
.
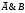3. Инверсия :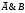 
.
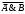Таким образом, структурной формулой данной функциональной схемы является формула:
.
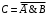Задача 2. Составить таблицу истинности для логической схемы:
Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы.
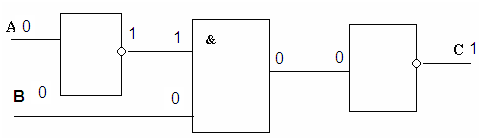
Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и преобразуются входные сигналы.
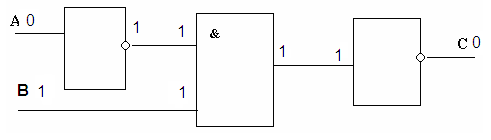
Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы.
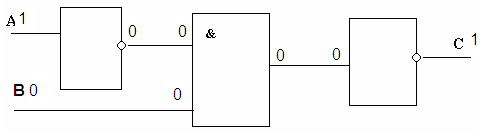
В результате получаем таблицу истинности данной логической схемы:
Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит арифметико-логическое устройство (АЛУ). Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах. Важнейшими из таких устройств являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.
Алгоритм конструирования логического устройства выглядит следующим образом:
Триггер (от английского слова trigger – защелка, спусковой крючок) – это электронное устройство, которое может находиться в одном из двух устойчивых состояний (1 или 0). Это означает, что триггер может хранить 1 бит информации.
Воздействуя на входы триггера, его переводят в одно из двух возможных состояний (0 или 1). С поступлением сигналов на входы триггера в зависимости от его состояния либо происходит переключение, либо исходное состояние сохраняется. При отсутствии входных сигналов триггер сохраняет свое состояние сколь угодно долго.
Полусумматор – логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров.Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел поразрядным сложением. Сумматор является центральным узлом арифметико-логического устройства процессора. Находит он применение и в других устройствах компьютера. Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то перенос суммируется с содержимым старшего соседнего разряда.
Таблица истинности
| А | В | AÚB |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Логическая операция «Конъюнкция» (логическое «и»). Конъюнкция АÙВ (A&B) – сложное высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно истинны.
Таблица истинности
| А | В | AÙB |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Логическая операция «Импликация». Импликация высказываний А и В (А®В) – сложное высказывание, которое истинно всегда, кроме случая когда А – истинно, а В – ложно.
Таблица истинности
| А | В | A→B |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Логическая операция «Эквивалентность» (двойная импликация).
Эквивалентность высказываний А и В (А«В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны либо ложны и ложно во всех других случаях.
Таблица истинности
| А | В | A→B |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Логические элементы. Логические элементы – устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого – «1» и низкого – «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже – на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Рассмотрим логические элементы.
Логический элемент НЕ (инвертор). Простейшим логическим элементом является инвертор, выполняющий функцию отрицания (инверсию). У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
| вход | выход |
| 1 | 0 |
| 0 | 1 |
Логический элемент ИЛИ (дизъюнктор). Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:
Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1.
| вход 1 | вход 2 | выход |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логический элемент И (конъюнктор). Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:
На выходе этого элемента будет сигнал 1 только в том случае, когда на все входы поступает сигнал 1. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
| вход 1 | вход 2 | выход |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Другие логические элементы построены из трех рассмотренных нами базовых элементов и выполняют более сложные логические преобразования информации. Рассмотрим примеры таких элементов.
Логический элемент И-НЕ. Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (И-НЕ). Имеет, как минимум, два входа. На функциональных схемах обозначается:
| вход 1 | вход 2 | выход |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
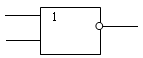
Логический элемент ИЛИ-НЕ. Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (И-НЕ). Имеет, как минимум, два входа. На функциональных схемах обозначается:
| вход 1 | вход 2 | выход |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов – функциональные схемы. Рассмотрим пример.
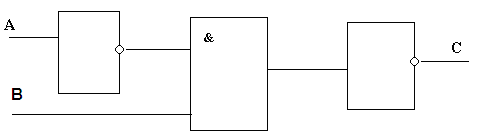
Задача 1. Записать логическую формулу для следующей функциональной схемы:
1. Инверсия ¬А:
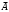.2
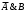. Логическое умножение значений ¬А и В: 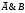.3. Инверсия
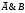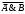: .Таким образом, структурной формулой данной функциональной схемы является формула:
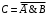.Задача 2. Составить таблицу истинности для логической схемы:
Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы.
Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и преобразуются входные сигналы.
Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы.
В результате получаем таблицу истинности данной логической схемы:
| А (вход 1) | В (вход 2) | С (выход) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит арифметико-логическое устройство (АЛУ). Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах. Важнейшими из таких устройств являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.
Алгоритм конструирования логического устройства выглядит следующим образом:
-
Построение таблицы истинности по заданным условиям работы проектируемого узла (т.е. по соответствию его входных и выходных сигналов). -
Конструирование логической функции данного узла по таблице истинности, ее преобразование (упрощение), если это возможно и необходимо. -
Составление функциональной схемы проектируемого узла по формуле логической функции.
Триггер (от английского слова trigger – защелка, спусковой крючок) – это электронное устройство, которое может находиться в одном из двух устойчивых состояний (1 или 0). Это означает, что триггер может хранить 1 бит информации.
Воздействуя на входы триггера, его переводят в одно из двух возможных состояний (0 или 1). С поступлением сигналов на входы триггера в зависимости от его состояния либо происходит переключение, либо исходное состояние сохраняется. При отсутствии входных сигналов триггер сохраняет свое состояние сколь угодно долго.
Полусумматор – логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров.Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел поразрядным сложением. Сумматор является центральным узлом арифметико-логического устройства процессора. Находит он применение и в других устройствах компьютера. Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то перенос суммируется с содержимым старшего соседнего разряда.