Файл: В юридической деятельности.docx

С целью упрощения процедуры перевода десятичных чисел в двоичные и для удобства восприятия полученного результата, целесообразнее исходное десятичное число перевести вначале в число, записанное в системе счисления с основанием, являющимся степенью числа 2 и наиболее близком к числу 10, а затем полученное число перевести в двоичное с помощью, очень простой процедуры. Такими системами счисления являются восьмеричная и шестнадцатеричная (2³<10<2⁴).

Таким образом, десятичное число вначале переводят в восьмеричную или шестнадцатеричную систему счисления, а затем полученное восьмеричное или шестнадцатеричное число – в двоичное. Такая процедура приводит к существенному уменьшению требуемых для кодирования операций деления.

В общем случае для перевода целых десятичных чисел в любую другую систему счисления используется метод последовательного деленияисходного числа на основание системы счисления, в которую переводится число. Полученный остаток после первого деления является младшим разрядом нового числа. Образовавшееся частное снова делится на это основание. Из остатка получаем следующий разряд нового числа и т.д. до тех пор, пока частное не станет равным нулю. Последний остаток от деления будет старшим разрядом искомого числа.

Приведем пример перевода числа 188₁₀ в восьмеричную систему счисления:

1 88	8
1 84	23	8
4	16	2	8
	7	0	0
		2	Старший разряд
188 (10) = 274 (8)

Рис. 4 Процедура перевода десятичного числа в восьмеричную форму

---

Перевод целых чисел из любой системы счисления с основанием q в десятичную осуществляется достаточно просто. Для этого надо записать исходное число в виде суммы степеней q и произвести указанные действия в десятичной системе счисления:

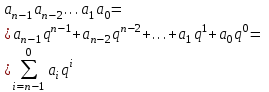(1)

Так, применяя формулу (1.5) для перевода восьмеричного числа 403_8, в десятичную систему счисления, получим (q=8):

403₈=4∙8²+0∙8¹+3∙8⁰=259₁₀,

для перевода шестнадцатеричного числа 14B₁₆ в десятичную систему получим (q=16):

14B₁₆=1∙16²+4∙16¹+B∙16⁰= 1∙16²+4∙16¹+11∙16⁰=331_10,

двоичное число 10001010₂ запишется в десятичной системе так (q=2):

10001010₂=1∙2⁷+0∙2⁶+0∙2⁵+0∙2⁴+1∙2³+0∙2²+1∙2¹+0∙2⁰ =138₁₀.

Арифметические операции во всех позиционных системах счисления выполняются по аналогичным правилам. Поэтому сложение двух чисел, например, в двоичной системе счисления, можно выполнять столбиком, начиная с младшего разряда и учитывая перенос единицы в старший разряд (1₂+1₂=10₂), например:

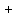1 00101 100111

1001100

Вычитание чисел в двоичной системе счисления выполняется также аналогично десятичной – столбиком, при этом надо занимать один разряд из следующего старшего разряда, если это необходимо (эта занимаемая единица в данном случае равна двум единицам данного разряда).

1 010001 101000

101001

Применение двоичной системы счисления в компьютере позволяет не только использовать простейшие устройства для представления информации, но и упростить схемы устройств, в которых выполняются арифметические операции (арифметические устройства) благодаря простоте правил двоичной арифметики.

Кодирование текстовой информации. Если каждому символу алфавита сопоставить определенное целое число (например, порядковый номер), то с помощью двоичного кода можно кодировать и текстовую информацию. Восьми двоичных разрядов достаточно для кодирования 256 различных символов. Этого хватит, чтобы выразить различными комбинациями восьми битов все символы английского и русского языков, как строчные, так и прописные, а также знаки препинания, символы основных арифметических действий и некоторые общепринятые специальные символы.

---

Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек различает символы по их начертанию, а компьютер – по их коду.

Важно, что присвоение символу конкретного кода – это вопрос соглашения, которое фиксируется в кодовой таблице. Кодирование текстовой информации с помощью байтов опирается на несколько различных стандартов, но первоосновой для всех стал стандарт ASCII (American Standart Code for Information Interchange), разработанный в США в Национальном институте ANSI (American National Standarts Institute). В системе ASCII закреплены две таблицы кодирования – базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.

Первые 33 кода (с 0 до 32) соответствуют не символам, а операциям (перевод строки, ввод пробела и т. д.).

Коды с 33 по 127 являются интернациональными и соответствуют символам латинского алфавита, цифрам, знакам арифметических операций и знакам препинания.

Коды с 128 по 255 являются национальными, т.е. в национальных кодировках одному и тому же коду соответствуют различные символы. В настоящее время существует много различных кодовых таблиц для русских букв (КОИ-8, СР1251, СР866, Mac, ISO), поэтому тексты, созданные в одной кодировке, могут не правильно отображаться в другой.

Кодирование изображений и звука. Информация, в том числе графическая и звуковая, может быть представлена в аналоговой или дискретной форме. При аналоговом представлении физическая величина принимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно. Примером аналогового представления графической информации может служить, скажем, живописное полотно, цвет которого изменяется непрерывно, а дискретного – изображение, напечатанное с помощью струйного принтера и состоящее из отдельных точек разного цвета. Примером аналогового хранения звуковой информации является виниловая пластинка (звуковая дорожка изменяет свою форму непрерывно), а дискретного – аудиокомпакт-диск (звуковая дорожка которого содержит участки с различной отражающей способностью). Графическая и звуковая информация из аналоговой формы в дискретную преобразуется путем

---

дискретизации, т.е. разбиения непрерывного графического изображения и непрерывного (аналогового) звукового сигнала на отдельные элементы. В процессе дискретизации производится кодирование, т.е. присвоение каждому элементу конкретного значения в форме кода.

Дискретизация – это преобразование непрерывных изображений и звука в набор дискретных значений, каждому из которых присваивается значение его кода.

3. Логические основы вычислений в компьютерных системах

Логика – это наука, изучающая формы и законы мышления, закономерности мыслительного процесса.

Логика изучает мышление как средство познания объективного мира. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира.

Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны.

Идеи и аппарат логики используется в кибернетике, вычислительной технике и электротехнике. Построение компьютеров также основано на законах математической логики.

В основе логических схем и устройств персонального компьютера лежит специальный математический аппарат, использующий законы логики. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.

Рассмотрим основные положения алгебры логики.

Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Высказыванием называется всякое утверждение, про которое всегда определенно и объективно можно сказать, является ли оно истинным или ложным. Высказывания могут быть простыми и сложными. Высказывание считается простым, если никакую его часть нельзя рассматривать как отдельное высказывание. Высказывание, которое можно разложить на части, будем называть сложным.

Алгебру логику называют также алгеброй Буля или булевой алгеброй, по имени английского математика Джорджа Буля

---

, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными буквами латинского алфавита. В алгебре Буля введены три основные логические операции с высказываниями: сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.

В качестве основных логических операций в сложных логических выражениях используются следующие:

• НЕ (логическое отрицание, инверсия);

• ИЛИ (логическое сложение, дизъюнкция);

• И (логическое умножение, конъюнкция).

Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение – двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно получить на основании основных операций.

Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении:

• 
  таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента – «истина» (1) и «ложь» (0) и два соответствующих им значения функции;
  
• 
  в таблице истинности двуместной логической операции – четыре строки: 4 различных сочетания значений аргументов – 00, 01, 10 и 11 и 4 соответствующих им значения функции;
  
• 
  если число высказываний в логическом выражении N, то таблица истинности будет содержать 2^N строк, так как существует 2^N различных комбинаций возможных значений аргументов.
  

Логическая операция «Инверсия» (отрицание; логическое «не»). Высказывание Ā (ØA) называется отрицанием высказывания А, если оно истинно, когда А ложно, и ложно, когда А истинно.

Таблица истинности

А	Ā
1	0
0	1

Логическая операция «Дизъюнкция» (логическое «или»).

---