Файл: Задача 1 2 Задача 2 3 Практическое задание 2 5 Задача 5 Практическое задание 3 12 Задача 12.docx

Практическое задание 4

Задача

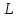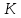Технологическая норма замещения факторов и равна 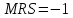. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактор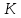а на 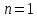единиц. Сколько дополнительных единиц фактора 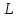потребуется фирме?

Решение:

Формула расчета технологической нормы замещения факторов 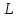и 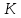имеет вид: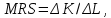



где 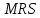– технологическая норма замещения факторов 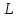и ;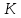

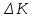– изменение количества применяемого в производственном процессе фактора 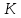; 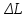– изменение количества применяемого в производственном процессе фактора .

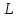Выражаем из этой формулы изменение количества фактора :





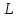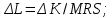
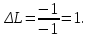
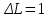единица фактора .

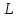Графическое решение представлено на рисунке.



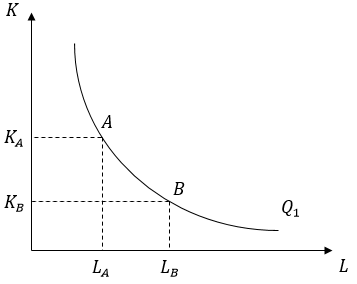
Рис. 4.1 – Изменение количества фактора 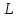при сокращении использования фактора

---

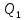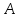Из рисунка следует, что если фирма желает остаться на прежней изокванте (линии равного выпуска) , то при сокращении использования фактора (смещении из точки в точку 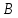) она должна вовлечь в производство дополнительное количество фактора .

Вывод: расчеты показывают, что количество использования фактора необходимо увеличить на 0,4 единицы.

Практическое задание 5

Задача 1

1. Предположим, что на рынке действуют две фирмы, функции общих издержек 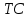заданы уравнениям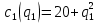и: и 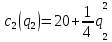. Рыночный спрос описывается функцией:

,

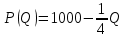где .

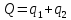Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:

- фирмы конкурируют по Курно;

- фирмы конкурируют по Бертрану;

- фирмы конкурируют по сценарию Штакельберга.

Изобразите решение на графике.

Решение:

В модели некооперированной дуополии Курно каждый дуополист исходит из предположения, что его соперник не изменит своего выпуска в ответ на его собственное решение. Это значит, что, принимая его, дуополист руководствуется стремлением к максимизации своей прибыли, полагая выпуск другого дуополиста заданным.

В данной модели состояние устойчивого равновесия в отрасли достигается в точке пересечения кривых реагирования дуополистов – точке равновесия Курно-Нэша. Кривые реагирования (кривые наилучшего ответа) – это множества точек наивысшей прибыли, которую может получить один из дуополистов при данной величине выпуска другого.

Представим функцию рыночного спроса в виде:



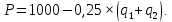
Выразим функции прибыли каждого из дуополистов:

---

;

.

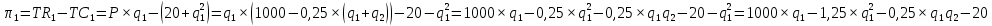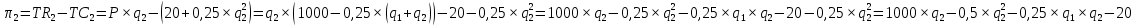Определим максимум полученных функций, найдя их первую производную и приравняв ее к 0:

;

.

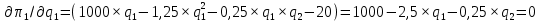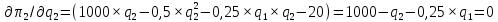Запишем уравнения кривых реагирования каждого из дуополистов, представив выпуск одного через выпуск другого.

Кривая реагирования дуополиста 1 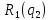имеет вид: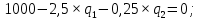







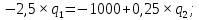
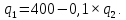
Кривая реагирования дуополиста 2 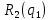представлена функцией: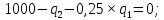







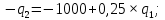
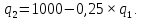
Оптимальные значения выпуска дуополистов в точке равновесия Курно-Нэша определяются точкой пересечения их кривых реагирования. Для нахождения оптимальных значений выпуска составим и решим систему уравнений:



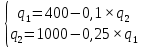
Подставляем 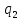в функцию для :









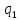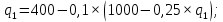
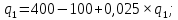
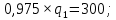
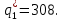
Тогда оптимальный выпуск дуополиста 2 составляет:





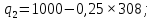
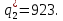
Следовательно, отраслевой выпуск равен:



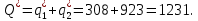
При оптимальных значениях выпуска дуополистов рыночная цена установится на уровне:

---

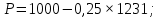
Графическая иллюстрация установления равновесия Курно-Нэша приведена на рисунке 5.1.



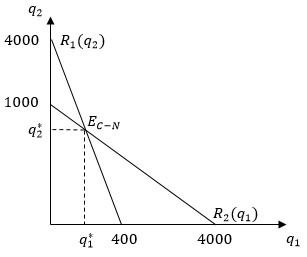
Рис. 5.1. Отраслевое равновесие в модели Курно

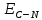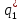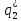На рисунке 5.1 кривые и – кривые реагирования дуополистов 1 и 2, соответственно; точка – точка равновесия Курно-Нэша; и – оптимальные объемы выпуска дуополистов 1 и 2, соответственно.

Модель дуополии Бертрана представляет собой модель ценовой, а не количественной дуополии. Для фирмы в дуополии Бертрана постоянным является не объем выпуска фирмы-конкурента, а назначаемая конкурентом цена. Анализ модели показывает, что в долгосрочном периоде дуополисты, конкурирующие по Бертрану, склонны вступать в состояние «ценовой войны», понижающее назначаемые ими цены до уровня их предельных издержек 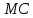, т.е. привило максимизации прибыли для каждого дуополиста принимает вид .

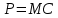Определим 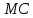как первую производную функции для каждого из дуополистов: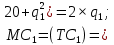





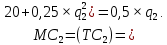
Приравняем к 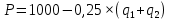, получая следующую систему уравнений: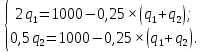



Выразим из первого уравнения: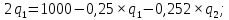

---

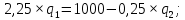
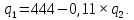
Подставляем во второе уравнение и находим оптимальный выпуск дуополиста 2: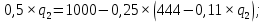









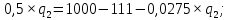
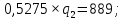
Тогда оптимальный выпуск дуополиста 1 составляет:







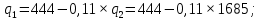
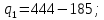
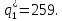
Следовательно, отраслевой выпуск равен:



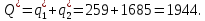
При оптимальных значениях выпуска дуополистов рыночная цена установится на уровне:





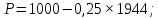
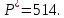
Графическая иллюстрация установления равновесия Бертрана-Нэша приведена на рисунке 5.2.



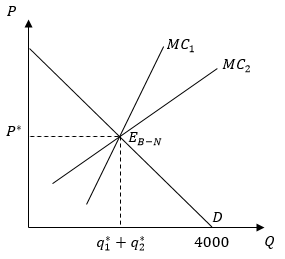
Рис. 5.2. Отраслевое равновесие в модели Бертрана

На рисунке 5.2 кривые 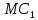и 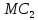– кривые предельных издержек дуополистов 1 и 2, соответственно; точка 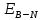– точка равновесия Бертрана-Нэша; и – оптимальные объемы выпуска дуополистов 1 и 2, соответственно.

Модель асимметричной дуополии Штакельберга предполагает, что каждый из дуополистов может придерживаться двух разных типов поведения: а) стремиться стать лидером или б) оставаться последователем. Фирма-последователь в данной модели придерживается предположений модели Курно – следует своей кривой реагирования и принимает решение о выпуске, полагая выпуск своего конкурента заданным. Фирма-лидер, напротив, знает функцию реагирования последователя и учитывает ее при выработке своей стратегии рыночного поведения

---