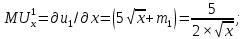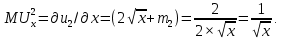Файл: Задача 1 2 Задача 2 3 Практическое задание 2 5 Задача 5 Практическое задание 3 12 Задача 12.docx
Добавлен: 10.01.2024
Просмотров: 176
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, действуя при этом подобно монополисту.
Предположим, что фирмой-лидером является дуополист 1.
Выпишем функцию прибыли лидера:
.
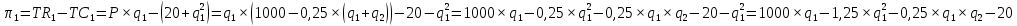Подставим вместо
в данное выражение полученную ранее функцию реагирования фирмы-последователя (дуополиста 2) 
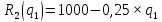и осуществим возможные преобразования:
.
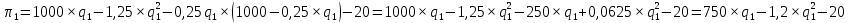Определяем максимум данной функции, находя ее первую производную и приравнивая ее к 0:
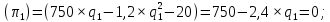
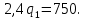
Отсюда оптимальный выпуск лидера равен:
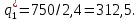
Оптимальный выпуск последователя можно получить, подставив полученный выпуск лидера в функцию реагирования последователя:
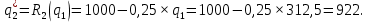
Следовательно, отраслевой выпуск равен:
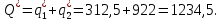
При оптимальных значениях выпуска дуополистов по Штакельбергу рыночная цена установится на уровне:
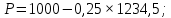
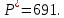
Рассуждая подобным же образом, находим оптимальный выпуск фирмы-лидера, если им является дуополист 2. Его функция прибыли:
.
Подставляем вместо
в данное выражение полученную ранее функцию реагирования фирмы-последователя (дуополиста 1)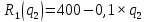 
и преобразуем его:
.
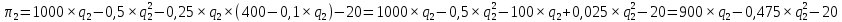Определяем максимум данной функции, находя ее первую производную и приравнивая ее к 0:
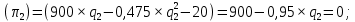
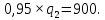
Отсюда оптимальный выпуск лидера равен:
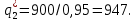
Оптимальный выпуск последователя получаем, подставляя рассчитанный выпуск лидера в функцию реагирования последователя:
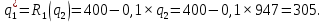
Следовательно, отраслевой выпуск равен:
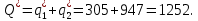
При оптимальных значениях выпуска дуополистов по Штакельбергу рыночная цена установится на уровне:
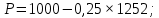
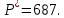
Графическая иллюстрация установления равновесия Штакельберга-Нэша приведена на рисунке 5.3.
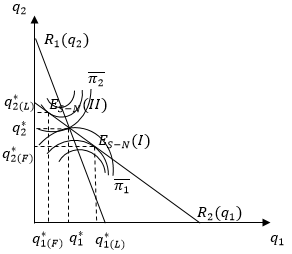
Рис. 5.3 – Отраслевое равновесие в модели Штакельберга
На рисунке 5.3 точка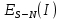
– точка равновесия в модели Штакельберга для случая, когда лидером является дуополист 1; точка 
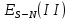– точка равновесия в модели Штакельберга для случая, когда лидером является дуополист 2; 
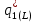и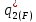 
– оптимальные выпуски в модели Штакельберга для случая, когда лидером является дуополист 1, а последователем – дуополист 2; 
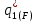и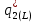 
– оптимальные выпуски в модели Штакельберга для случая, когда лидером является дуополист 2, а последователем – дуополист 1; кривые 
и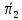 
– изопрофиты (линии равной прибыли) дуополистов 1 и 2, позволяющие найти точки равновесия Штакельберга-Нэша как точки, в которых кривые реагирования являются касательными к соответствующим кривым реагирования фирм.
Вывод: Отраслевой выпуск в случае конкуренции дуополистов по модели Курно ниже, а рыночная цена – выше, чем когда дуополисты конкурируют по Бертрану. Результаты конкуренции по модели Штакельберга подобны таковым в модели Курно, однако фирма-лидер в этой модели получает возможность захватить большую часть рынка за счет части рыночного спроса на продукцию своего конкурента.
График предельных издержек фирмы-монополиста задан условием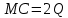
. Функция предельного дохода принимает вид: 
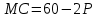. Определите эластичность рыночного спроса 
при оптимальном выпуске фирмы-монополиста.
Решение:
Условие максимизации прибыли фирмой-монополистом имеет вид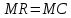
:
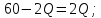
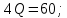
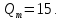
Для линейной кривой спроса вида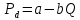
функция предельного дохода имеет вид:
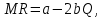
где
– свободный член уравнения; 
– коэффициент угла наклона функции спроса.
Следовательно, функция спроса на продукцию монополиста может быть представлена уравнением:
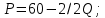
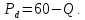
Определяем цену, которую назначит монополист на свою продукцию, подставляя в полученную функцию спроса величину оптимального выпуска:
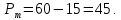
Эластичность в точке оптимума монополиста рассчитаем по формуле точечной эластичности спроса по цене:
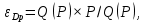
где – коэффициент эластичности спроса на благо по его цене;
– первая производная функции спроса по параметру цены 
; 
– уравнение кривой спроса.
Представим функцию спроса в виде прямой:
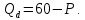
Находим производную функции спроса по :
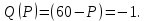
Тогда эластичность спроса по цене в точке максимизации монополистом своей прибыли равна:
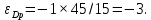
Предположим, что издержки по вывозу мусора с территории двух районов составляют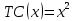
, где 
– площадь территории. Проведенные исследования выявили, что предпочтения всех жителей 1-го района принимают вид функции полезности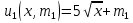 
, а предпочтения всех жителей 2-го района – 
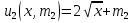, где 
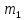и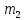 
– потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.
Найдите Парето-эффективное значение вывоза мусора с районов. Изобразите решение задачи на графике.
Решение:
Поскольку функции полезности потребителей заданы как квазилинейные, то условие определения Парето-оптимального значения производства общественного блага принимает вид:
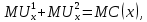
где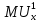
– предельная полезность общественного блага для первой группы потребителей; 
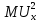– предельная полезность общественного блага для второй группы потребителей; 
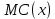– предельные издержки производства общественного блага.
Находим предельные полезности:
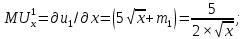
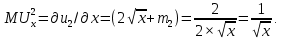
Предположим, что фирмой-лидером является дуополист 1.
Выпишем функцию прибыли лидера:
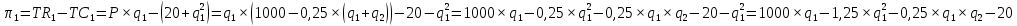.Подставим вместо
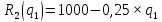в данное выражение полученную ранее функцию реагирования фирмы-последователя (дуополиста 2) и осуществим возможные преобразования: 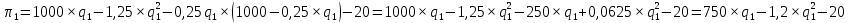.Определяем максимум данной функции, находя ее первую производную и приравнивая ее к 0:
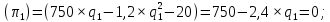
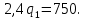
Отсюда оптимальный выпуск лидера равен:
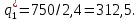
Оптимальный выпуск последователя можно получить, подставив полученный выпуск лидера в функцию реагирования последователя:
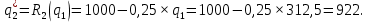
Следовательно, отраслевой выпуск равен:
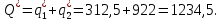
При оптимальных значениях выпуска дуополистов по Штакельбергу рыночная цена установится на уровне:
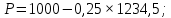
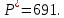
Рассуждая подобным же образом, находим оптимальный выпуск фирмы-лидера, если им является дуополист 2. Его функция прибыли:
.Подставляем вместо
в данное выражение полученную ранее функцию реагирования фирмы-последователя (дуополиста 1) 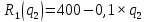и преобразуем его: 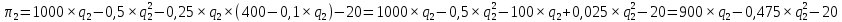.Определяем максимум данной функции, находя ее первую производную и приравнивая ее к 0:
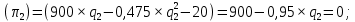
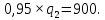
Отсюда оптимальный выпуск лидера равен:
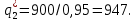
Оптимальный выпуск последователя получаем, подставляя рассчитанный выпуск лидера в функцию реагирования последователя:
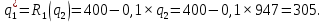
Следовательно, отраслевой выпуск равен:
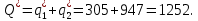
При оптимальных значениях выпуска дуополистов по Штакельбергу рыночная цена установится на уровне:
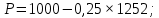
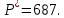
Графическая иллюстрация установления равновесия Штакельберга-Нэша приведена на рисунке 5.3.
Рис. 5.3 – Отраслевое равновесие в модели Штакельберга
На рисунке 5.3 точка
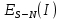– точка равновесия в модели Штакельберга для случая, когда лидером является дуополист 1; точка 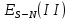– точка равновесия в модели Штакельберга для случая, когда лидером является дуополист 2; 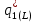и 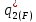– оптимальные выпуски в модели Штакельберга для случая, когда лидером является дуополист 1, а последователем – дуополист 2; 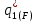и 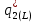– оптимальные выпуски в модели Штакельберга для случая, когда лидером является дуополист 2, а последователем – дуополист 1; кривые и 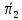– изопрофиты (линии равной прибыли) дуополистов 1 и 2, позволяющие найти точки равновесия Штакельберга-Нэша как точки, в которых кривые реагирования являются касательными к соответствующим кривым реагирования фирм.Вывод: Отраслевой выпуск в случае конкуренции дуополистов по модели Курно ниже, а рыночная цена – выше, чем когда дуополисты конкурируют по Бертрану. Результаты конкуренции по модели Штакельберга подобны таковым в модели Курно, однако фирма-лидер в этой модели получает возможность захватить большую часть рынка за счет части рыночного спроса на продукцию своего конкурента.
Задача 2
График предельных издержек фирмы-монополиста задан условием
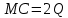. Функция предельного дохода принимает вид: 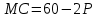. Определите эластичность рыночного спроса при оптимальном выпуске фирмы-монополиста.Решение:
Условие максимизации прибыли фирмой-монополистом имеет вид
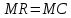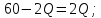
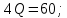
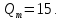
: Для линейной кривой спроса вида
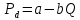функция предельного дохода имеет вид: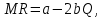 где
– свободный член уравнения; – коэффициент угла наклона функции спроса.Следовательно, функция спроса на продукцию монополиста может быть представлена уравнением:
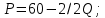
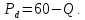
Определяем цену, которую назначит монополист на свою продукцию, подставляя в полученную функцию спроса величину оптимального выпуска:
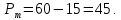
Эластичность в точке оптимума монополиста рассчитаем по формуле точечной эластичности спроса по цене:
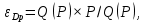
где
– коэффициент эластичности спроса на благо по его цене; – первая производная функции спроса по параметру цены ; – уравнение кривой спроса.Представим функцию спроса в виде прямой:
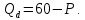
Находим производную функции спроса по
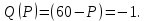
: Тогда эластичность спроса по цене в точке максимизации монополистом своей прибыли равна:
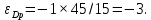
Практическое задание 6
Задача
Предположим, что издержки по вывозу мусора с территории двух районов составляют
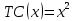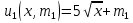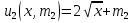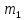, где – площадь территории. Проведенные исследования выявили, что предпочтения всех жителей 1-го района принимают вид функции полезности , а предпочтения всех жителей 2-го района – , где и 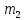– потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.Найдите Парето-эффективное значение вывоза мусора с районов. Изобразите решение задачи на графике.
Решение:
Поскольку функции полезности потребителей заданы как квазилинейные, то условие определения Парето-оптимального значения производства общественного блага принимает вид:
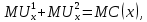
где
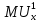– предельная полезность общественного блага для первой группы потребителей; 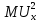– предельная полезность общественного блага для второй группы потребителей; 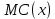– предельные издержки производства общественного блага.Находим предельные полезности: