Файл: 1 Задача 1С Плоская система сходящихся сил 3 2 Задача 2С Плоская система произвольно расположенных сил 5.docx
Добавлен: 10.01.2024
Просмотров: 107
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Задача 1-С: Плоская система сходящихся сил
2 Задача 2-С: Плоская система произвольно расположенных сил
3 Задача 3-С: Плоская система произвольно расположенных сил
4 Задача 4-С: Плоская система произвольно расположенных сил
5 Задача 5-С: Пространственная система произвольно расположенных сил

СОДЕРЖАНИЕ
1 Задача 1-С: Плоская система сходящихся сил 3
2 Задача 2-С: Плоская система произвольно расположенных сил 5
1 Задача 1-С: Плоская система сходящихся сил
Условие. Грузы весом G1, G2и G3находятся в равновесии. Известны вес груза G2=55 Н и углы α=75°, β=60°. Определить вес груза G3.
С
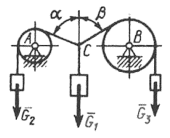
хема по заданию.
Решение.
Выбираем правую плоскую декартовую систему координат и составляем расчетную схему (рисунок 1).
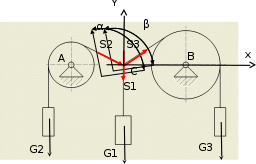
Рисунок 1 Расчетная схема
Реакции связей направлены по тросам от узла С соединения тросов. Реакция S1будет направлена в направлении блока 1 и трос будет растянут. Реакция S2будет направлена вниз, а S3 в направлении блока 2 троса будут растянуты.
Начало координат возьмем в точке пересечения С действующих сил. Следовательно, получаем плоскую систему сходящихся сил.
Запишем уравнение равновесия:
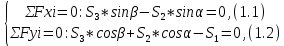
Поскольку в исходных данных не задан вес G1, то уравнение два рассматривать нет смысла.
Тогда из уравнения (1) находим усилие S3, которое и будет равно весу G3.
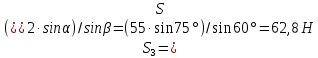
Ответ G3= 62,8 H.
2 Задача 2-С: Плоская система произвольно расположенных сил
Условие. На жесткую раму действует пара сил с моментом M=60 H‧м и две силы F1=10 H приложена в точке К под углом α1=30о и F4= 40 H приложена в точке H под углом α4=60о . Cхема рамы рис. 5, a=0,5 м.
Определить реакции связей (опорные реакции) в точках А и В с помощью аналитических условий равновесия. Убедиться в правильности решения
, выполнив проверку.
Схема рамы показана на рисунке 2.1.
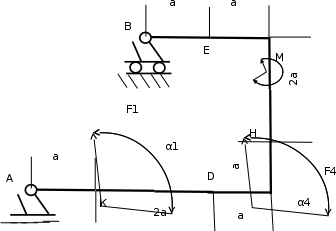
Рисунок 2.1 –Схема жесткой рамы
Решение.
Выбираем правую плоскую декартовую систему координат и составляем расчетную схему (рисунок 2.2).
В точке А шарнирно-неподвижная опора, поэтому неизвестную силу реакции связи ????А раскладываем на составляющие, параллельные осям координат.
????А=????????А+????????А
В точке В шарнирно-подвижная опора. Неизвестную силу реакции связи ????В направляем по нормали к опорной поверхности.
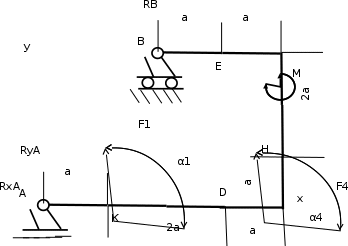
Рисунок 2.2 –Расчетная схема жесткой рамы
 Записываем условия равновесия плоской системы в аналитической форме.
Записываем условия равновесия плоской системы в аналитической форме. Σ????????????=0 : ????????????+????4∙sin????4+????1∙cos????1=0 (2.1)
Σ????????????=0 : ????????????+????4∙sin????4+????1∙cos????1=0 (2.1) Σ????????????=0 : ????????????−????4∙cos????4+????1∙sin????1+????????=0 (2.2)
Σ????????(????????)=0 : −????4∙sin????4∙????−????4∙cos????4∙4????+????1∙sin????1∙????+
+????????∙2????−????=0 (2.3)
Решаем систему из трех уравнений.
Из уравнения (2.1) получаем:
????????????=−????4∙sin ????4 − ????1∙cos ????1= −40∙sin 60−10∙cos 30 = −40∙0,866 − 10∙0,866 = =−43,3 ????.
Из уравнения (2.3) получаем:
???????? = (????4∙sin????4∙???? + ????4∙cos????4∙4???? − ????1∙sin????1∙???? + ????)/2a = (40∙sin60∙0,5 + 40∙cos60∙4∙0,5 − 10∙sin30∙0,5 + 60)/2∙0,5 = (40∙0,866∙0,5 + 40∙0,5∙4∙0,5 – 10∙0,5∙0,5 +60)/1= 17,32+69,28+60=114,82 H.
Из уравнения (2.2) получаем:
????????????=????4∙cos ????4−????1∙sin ????1−????????= 40∙0,5 − 10∙0,5 −144,1= 20–5–144,1 =
= -99,82 ????.
Выполняем проверку:
Σ????H(????????)=0 : ????????????∙????−????????????∙4????+????1∙cos????1∙????−????1∙sin????1∙3????−????????∙2????−????=
=(−43,3)∙0,5−(-99,82)∙4∙0,5+10∙0,866∙0,5−10∙0,5∙3∙0,5−114,82∙2∙0,5−60=0.
О
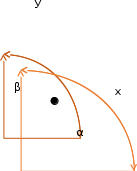 пределяем величину реакции связи ????????
пределяем величину реакции связи ???????? 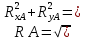
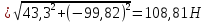
Значениeи RxA RyA получились отрицательными. Это указывает на то, что принятые направления этой силы противоположны их действительным направлениям.

Рисунок 2.3 – Схема для определения направления RA
Направление RA найдем по направляющим косинусам.
cos????=????????????/????????= −4 3,3/108,81=−0,3979 => ????=113,45°
cos????=????????????/????????=−99,82/108,81=−0,9174 => ????=156,55°
Ответ: RA = 108,81 H, RB = 114,82 H.
3 Задача 3-С: Плоская система произвольно расположенных сил
Условие. На жесткую раму действуют силы, указанные в таблице 3.. Схема конструкции рамы представлена на рисунке3.1. Размеры стержней указаны в м.
Определить реакции связей (опорные реакции) в конструкции с помощью аналитических условий равновесия. Убедиться в правильности решения, выполнив проверку.
Таблица 3.1. Исходные данные.
| № вар. | G, кН | P, кН | M, кН·м | q, кН/м | α, град. |
| 18 | 20 | 10 | 10 | - | 30 |
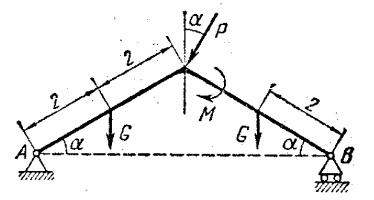
Рисунок 3.1 - Схема конструкции рамы
Решение:
Выбираем правую плоскую декартовую систему координат и составляем расчетную схему (рисунок 3.2).
В точке А шарнирно-неподвижная опора, поэтому неизвестную силу реакции связи ???????? раскладываем на составляющие, параллельные осям координат.
????????=????????????+???????????? , (3.1)
В точке В шарнирно-подвижная опора. Неизвестную силу реакции связи ????В направляем по нормали к опорной поверхности.

2
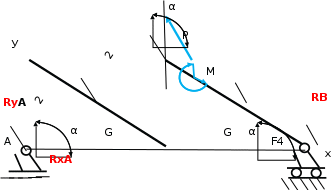
Рисунок 3.2 – Расчетная схема конструкции рамы
Записываем условия равновесия плоской системы в аналитической форме.
Σ????????????=0 : ????????????−P∙sin????=0 , (3.1)
Σ????????????=0 : ????????????−2????−P∙cos????+RB=0, (3.2)
Σ????????(????????)=0 : −????∙2 cos????−P∙cos????∙4∙ cosα+ P∙sin????∙4∙sinα –
−????∙6∙cos???? − ????+RB∙6∙cosα=0 , (3.3)
Решаем систему из трех уравнений.
Из уравнения (3.1) получаем
????????????=P∙sin 30 = 10∙0,5=5 ????????.
Из уравнения (3.3) получаем
RB=(????∙2cos????+P∙cos????∙4∙cosα−P∙sin????∙4∙sin????+????∙6∙cos????+????)/8∙cosα= (20∙0,866∙2+10∙0,866∙4∙0,866–10∙0,5∙4∙0,5+20∙6∙0,866+10)/8∙0,866=24,33
кН.
Из уравнения (3.2) получаем
????????????=2????+P∙cos????-RB=2 ∙20 +10 ∙0,866–24,33=24,33 кН
Выполняем проверку:
Σ????P(????????)=0 :
-RyA∙4∙cosα+RxA∙4∙sinα+G∙2∙cosα–G∙2∙cosα+RB∙4∙cosα-М=-24,33∙4∙0,866+5∙4∙0,5+20∙2∙0,866-20∙2∙0,866+24,33∙4∙0,866-10=0.
Определяем величину реакции связи ????????
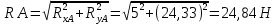
Значения RxA и RyA получились положительными. Это указывает на то, что принятые направления этих сил совпадают с их действительными направлениями.
Направление RA найдем по направляющим косинусам.
cos????=????????????/????????= 5/24,84=0,2012 => ????=78,4°
cos????=????????????/????????=24,33/24,84=−0,9795 => ????=11,6°
О
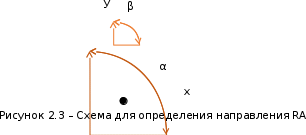
твет: RA = 24,84 H, RB = 24,33 H.
4 Задача 4-С: Плоская система произвольно расположенных сил
Условие: На жесткую раму действуют силы, указанные в таблице 4.1. Схема конструкции рамы представлена на рисунке 4.1. Размеры стержней указаны в м.
Определить реакции связей (опорные реакции) и давление в промежуточном шарнире составной конструкции (система двух тел) с помощью аналитических условий равновесия. Убедиться в правильности решения, выполнив проверку.
Таблица 4.1. Исходные данные.
| № вар. | P1, кН | P2, кН | M, кН·м | q, кН/м |
| 18 | 7 | 16 | 27 | 0,8 |
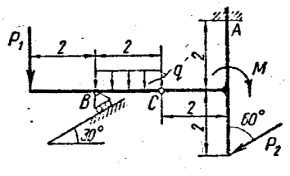
Рисунок 4.1 - Схема конструкции рамы
Решение. Выбираем правую плоскую декартовую систему координат и составляем расчетную схему.
Согласно аксиоме о связях в точках А и В вместо связей изображаем силы реакции связей.
В точке В шарнирно-подвижная опора. Неизвестную силу реакции связи ????В направляем по нормали к опорной поверхности.
В точке А заделка, поэтому неизвестные силы реакции ???????? раскладываем на составляющие, параллельные осям координат. А также там прикладывается момент МВ.
????????=????????????
+???????????? , (4.1)
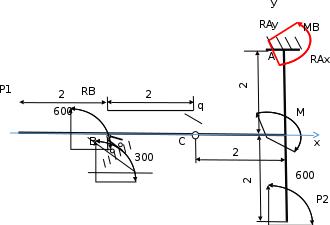
Рисунок 4.2 – Расчетная схема конструкции
Сначала записываем условия равновесия плоской системы в аналитической форме для всей конструкции.
Σ????????????=0 : −RB∙cos60+R????x−P2∙ sin60 =0 (4.1)
Σ????????????=0 : −????1+ RB∙sin60+R????y−q 2−????2∙cos60=0 (4.2)
Σ????????(????????)=0 : ????1∙6−RB∙sin60∙4− RB∙cos60∙2 +????∙2∙3−????−
−????2∙sin60∙4+MB=0 (4.3)
Решить систему не представляется возможным, поэтому разобьем составную конструкцию на две по шарниру (правую (рисунок 4.3) и левую (рисунок 4.4)). Усилие (давление) в шарнире ???????? раскладываем на составляющие, параллельные осям координат.
????????=????????????+???????????? , (4.4)
Усилия ???????????? и ???????????? в шарнире правой части конструкции равны по величине и противоположны по направлению усилиям в левой части конструкции. Если снова соединить две части конструкции, то давление в шарнире будет = 0.
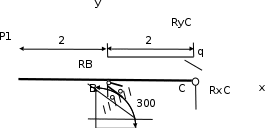
Рисунок 4.3 – Расчетная схема конструкции (левая)
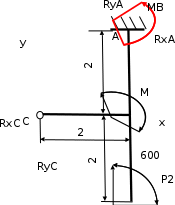
Рисунок 4.4 – Расчетная схема конструкции (правая)
Записываем условия равновесия плоской системы в аналитической форме для левой части конструкции.
Σ????????????=0 : ????????????−????????∙cos60=0 (4.5)
Σ????????????=0 : ????????????−????1+????????∙sin60–q∙2=0 (4.6)
Σ????с(????????)=0 : − ????????∙sin60∙2+????1∙4 + q∙2∙1=0 (4.7)
Из уравнения (4.7) получаем
????В=(–????1∙4 – q∙2∙1)/(2∙0,866)=(–7∙4 – 0,8∙2∙1)/2∙0,866=17,1 кН.
Из уравнения (4.6) получаем
????yC =(−????B sin60+????1+q∙2)= −17,1 0,866+7+0,8∙2=−6,2 кН.
Из уравнения (4.5) получаем
????????????=????????∙cos60=17,1∙0,5=8,55 кН.
Выполняем проверку:
Σ????B(????????)=0 :
P1∙2−q∙2∙1+RyC∙2= 7∙2−0,8∙2 1+(−6,2∙2)=14−1,6−12,4=0.
Возвращаемся к решению уравнения (4.1)
R????x =RB∙cos60+P2∙sin60 =17,1∙0,5+16∙0,866=22,406 кН.
Из уравнения (4.2) получаем
Ry????=????1− RB∙sin60+ q 2+????2∙cos60=7−17,1 0,866+0,8 2+16 0,5=1,7914 кН
Из уравнения (4.3) получаем
MB =−????1∙6+RB∙sin60∙4+RB∙cos60∙2 −????∙2∙3+????+????2