Файл: 1 Задача 1С Плоская система сходящихся сил 3 2 Задача 2С Плоская система произвольно расположенных сил 5.docx
Добавлен: 10.01.2024
Просмотров: 112
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Задача 1-С: Плоская система сходящихся сил
2 Задача 2-С: Плоская система произвольно расположенных сил
3 Задача 3-С: Плоская система произвольно расположенных сил
4 Задача 4-С: Плоская система произвольно расположенных сил
5 Задача 5-С: Пространственная система произвольно расположенных сил
∙sin60∙4= −7∙6+17,1∙0,866∙4+17,1∙0,5∙2−0,8∙2∙3+27+16∙0,866∙4=111,9584 кНм
Выполняем проверку:
Σ????B(????????)=0 :
P1∙2–q∙2∙1 – RxA∙2+RyA∙4+MB–M–P2∙cos60∙4-P2∙sin60∙2=7∙2 – 0,8∙2 – 22,406∙2+1,7914∙4+111,9584 – 27 - 16∙0,5∙4 - 16∙0,866∙2= 0
Определяем величину усилия (давление) в шарнире ????????
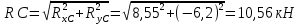
Определяем величину усилия ????А
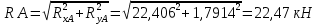
Ответ: Rc=10.56 кН; RA= 22,47 кН;RВ=17,1 кН; МВ=111,9584 кНм.
Плита весом P=3 кН со сторонами AB=3a, BC=2a закреплена в точке А сферическим, а в точке В цилиндрическим шарниром и удерживается в равновесии невесомым стержнем CC’ (Рисунок 5.1). На плиту действует пара сил с моментом М=5 кН·м, лежащая в плоскости плиты, и две силы (номера, величины, направление и точки приложения сил приведены в таблице 5.1). Точки приложения сил D, E, H находятся на серединах сторон плиты, a=0,8 м.
Определить реакции связей (опорные реакции) в точках А, В и С.
Таблица 5.1 Направления и точки приложения сил
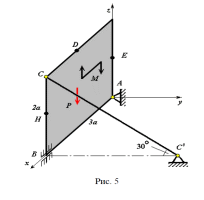
Рисунок 5.1 Схема закрепления плиты
Решение.
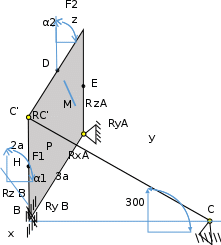
Выбираем правую пространственную декартовую систему координат с началом в точке А и составляем расчетную схему.
Согласно аксиоме о связях в точках А, В и С вместо связей изображаем силы реакции связей. В точке А сферический шарнир, поэтому неизвестную силу реакции связи ???????? раскладываем на три составляющие, параллельные осям координат.
????????=????????????+????????????+???????????? , (5.1)
В точке B цилиндрический шарнир, поэтому неизвестную силу реакции связи ???????? раскладываем на две составляющие, лежащие в плоскости, перпендикулярной оси шарнира.
????????=????????????+???????????? , (5.2)
В точке С невесомый стержень CC’. Неизвестную силу реакции стержня ????С направляем вдоль стержня.
Σ????????????=0 : ????????????−????2∙sin????2 =0 (5.3)
Σ????????????=0 : ????????????+????????????+????1+Rc’∙cos30 =0 (5.4)
Σ????????????=0 : ????????????+????????????−????????∙sin30+????2∙cos????2−????=0 (5.5)
Σ????????????(????????)=0 : −????????∙cos30∙2????−????1∙????=0 (5.6)
Σ????????????(????????)=0 : −????????????∙3????+????????∙sin30∙3????−????2∙cos????2∙1,5????+????∙1,5????−M=0 (5.7)
Σ????????????(????????)=0 : ????????????∙3????+????1∙3????+????????∙cos30∙3????=0 (5.8)
Решаем систему из шести уравнений.
Из уравнения (5.3) получим
????????????=????2∙sin????2 = 6∙sin30=3 кН
Из уравнения (5.6) получим
????????=−????1∙????/(cos30∙2????) = −4∙0,8 /(0,866∙2∙0,8)=2,31 Н
Из уравнения (5.8) получим
????????????=(−????1∙3????−????????∙cos30∙3????)/3???? =−????1−????????∙cos30==−4−2,31∙0,866=−6,0005 кН
Из уравнения (5.7) получим
????????????=(????????∙sin30∙3????−????2∙cos????2∙1,5????+????∙1,5????−M)/3а=(2,31∙0,5∙3∙0,8−6∙0,866∙1,5∙0,8+
+3∙1,5∙0,8−5)/3∙0,8=(2,772−6,2352+3,6−5)/2,4=−2,026 кН
Из уравнения (5.5) получим
????????????=−????????????+????????∙sin30−????2∙cos????2+????=2,026+ 2,31∙0,5−6∙0,866+3=0,985 кН
Из уравнения (5.4) получим
????????????=−????????????−????1−Rc’∙cos30= ????????????=6−4−2,31∙0,866= -0,0005 кН
Чтобы убедиться в правильности нахождения опорных реакций, составим проверочные уравнения. Для этого перенесем начало нашей системы координат в точку, где приложен вес плиты.
Σ????????????(????????)=0 :
????????????∙1,5????−????????????∙1,5????+????????∙sin30∙1,5????−М=0,985∙1,5∙0,8+2,026∙1,5∙0,8+2,31∙0,5∙1,5∙0,8−5= =0,0008≈0
Полученная цифра в четвертом знаке после запятой могла получиться потому, что в процессе расчета полученные значения округлялись.
Поэтому можно сделать вывод что проверка сошлась.
Σ????????????(????????)=0 :
−????????????∙1,5????+????????????∙1,5????+????1∙1,5????+????????∙cos30∙1,5????=0,0005∙1,5∙0,8+(−6,0005)∙1,5∙0,8+
+4∙1,5∙0,8+ 2,31∙0,866∙1,5∙0,8=−0,0004≈0
Проверка сошлась.
Определяем величину и направление реакции связи ????????
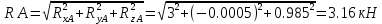
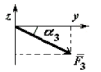
cos????=????????????/????????=3/3,16=−0,949 => ????=18,3°
cos????=????????????/????????=−0,0005/3,16=−0,00015 => ????=90,01°
cos????=????????????/????????=0,985/3,16= 0,312 => ????=71,84°
Определяем величину и направление реакции связи ????B
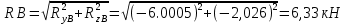
cos????=????????B/????B=−6,0005/6,33=−0,9479 => ????=161,43°
cos????=????????B/????B=−2,026/6,33= −0,32 => ????=108,67°
Ответ: RA = 3,16 kH, RB = 6,33 kH, RС= 2,31 kH.
Плоский механизм состоит из стержней 1 – 4 и ползуна В, соединенных друг с другом и с неподвижными опорами O1 и O2 шарнирами (рис. 6.1). Длины стержней равны: l1=0,4 м, l2=1,2 м, l3=1,4 м, l4=0,8 м. Положение механизма определяется углами α, β, γ, φ, θ (см. таблицу 6.1). Точка D находится в середине соответствующего стержня.
Определить величины указанные в таблице 6.1 в столбце «Найти».
Таблица 6.1.
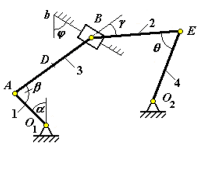
Рисунок 6.1 – Схема плоского механизма
Условие: Пластина (рисунок 7.1) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в таблице 7.1 (при знаке минус направление ω противоположно показанному на рисунке). Ось вращения OO1, лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка М. Закон ее относительного движения задается уравнением S = AM = f(t), (S – в сантиметрах, t – в секундах), приведенным в таблице 6.1. На всех рисунках точка М показана в положении, при котором S = AM > 0 (при S < 0 точка М находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 c.
Таблица 7.1
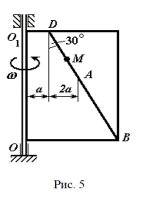
Рисунок 7.1 – Вращающаяся пластина
Решение. Рассмотрим движение точки М как сложное: относительное движение – поступательное движение точки М вдоль прямой BD, переносное движение – вращательное движение точки М вместе с пластиной вокруг неподвижной оси ОО1. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:
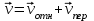, (7.1)
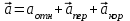, (7.2)
или в развернутом виде
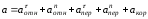. (7.3)
Определим положение точки М на прямой .
S = AM= f(t)=60∙ (t3−2t2), (7.4)
Для этого подставим в уравнение (7.4) относительного движения точки время t=1c. подучим
МSt=1 = AM= 60∙ (13−2∙ 12)= −60 cм.
Так как S < 0, то точка М находится по другую сторону от точки А. в области отрицательных значений на отрезке АВ.Выполняем рисунок с необходимыми построениями.
Рассмотрим относительное движение точки М.
Чтобы найти относительную скорость точки М необходимо продифференцировать перемещение по времени. Для этого возьмем первую производную выражения (7.4).
Получим
????отн=????????/????????=(60∙(????3−2????2))′=60∙(3????2−4????),
При t = 1 c получаем
????отн=60∙(3????2−4????)=60∙(3∙12−4∙1)=−60 см/с,
Знак минус говорит о том, что вектор относительной скорости направляем от точки М к точке В. В область отрицательных значений S. Проверить правильность выбора направления скорости можно, подставив в формулу пути другое время, например t = 1,1 с:
???? ????=1,1 =????????=60∙(????3−2????2)=60∙(1,13−2∙1,12)=−65,34 см.
Модуль относительной скорости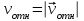
=60 см/с.
Модуль относительного касательного ускорения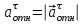
, где
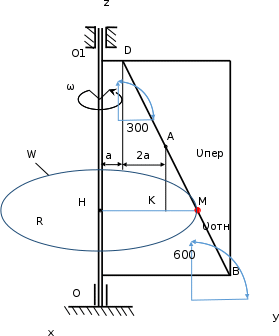
Рисунок 7.2 – Расчетнаясхема
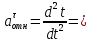(60∙(????3−2????2))′′= 60∙(6????−4).
При t = 1 c получаем
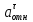=60∙(6????−4)=60∙(6∙1−4)=120 см/с2.
Значит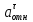 =120 см/с2.
Вектор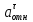 направлен в сторону положительных значений, т.к. знаки скорости и ускорения разные, следовательно, относительное движение точки М замедленное.
Относительное нормальное ускорение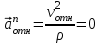
, так как траектория относительного движения – прямая линия (
).
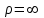Определяем переносную скорость ????e . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO1.
Из точки M опустим перпендикуляр HM на ось OO1.
При переносном движении точка M движется по окружности W (hbceyjr 7/2) радиуса R=HM с центром в точке H.
R=HM = HK + KM = 3a + |AM| sin 30° = 60 + 60·0,5 = 90 см;
Переносное движение:
Переносная скорость точки М перпендикулярна отрезку HМ и равна:
Выполняем проверку:
Σ????B(????????)=0 :
P1∙2–q∙2∙1 – RxA∙2+RyA∙4+MB–M–P2∙cos60∙4-P2∙sin60∙2=7∙2 – 0,8∙2 – 22,406∙2+1,7914∙4+111,9584 – 27 - 16∙0,5∙4 - 16∙0,866∙2= 0
Определяем величину усилия (давление) в шарнире ????????
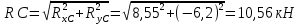
Определяем величину усилия ????А
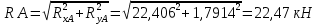
Ответ: Rc=10.56 кН; RA= 22,47 кН;RВ=17,1 кН; МВ=111,9584 кНм.
5 Задача 5-С: Пространственная система произвольно расположенных сил
Плита весом P=3 кН со сторонами AB=3a, BC=2a закреплена в точке А сферическим, а в точке В цилиндрическим шарниром и удерживается в равновесии невесомым стержнем CC’ (Рисунок 5.1). На плиту действует пара сил с моментом М=5 кН·м, лежащая в плоскости плиты, и две силы (номера, величины, направление и точки приложения сил приведены в таблице 5.1). Точки приложения сил D, E, H находятся на серединах сторон плиты, a=0,8 м.
Определить реакции связей (опорные реакции) в точках А, В и С.
Таблица 5.1 Направления и точки приложения сил
| № вар. | Сила | № рис. | ||||||||
 |  |  |  | |||||||
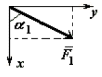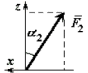| F1 = 4 кН | F2 = 6 кН | F3 = 8 кН | F4 = 10 кН | |||||||
| Точка прил-я | α1,° | Точка прил-я | α2,° | Точка прил-я | α3,° | Точка прил-я | α4,° | |||
| 18 | H | 90 | D | 30 | - | - | - | - | 5 | |
Рисунок 5.1 Схема закрепления плиты
Решение.
Выбираем правую пространственную декартовую систему координат с началом в точке А и составляем расчетную схему.
Согласно аксиоме о связях в точках А, В и С вместо связей изображаем силы реакции связей. В точке А сферический шарнир, поэтому неизвестную силу реакции связи ???????? раскладываем на три составляющие, параллельные осям координат.
????????=????????????+????????????+???????????? , (5.1)В точке B цилиндрический шарнир, поэтому неизвестную силу реакции связи ???????? раскладываем на две составляющие, лежащие в плоскости, перпендикулярной оси шарнира.
????????=????????????+???????????? , (5.2)
В точке С невесомый стержень CC’. Неизвестную силу реакции стержня ????С направляем вдоль стержня.
Σ????????????=0 : ????????????−????2∙sin????2 =0 (5.3)
Σ????????????=0 : ????????????+????????????+????1+Rc’∙cos30 =0 (5.4)
Σ????????????=0 : ????????????+????????????−????????∙sin30+????2∙cos????2−????=0 (5.5)
Σ????????????(????????)=0 : −????????∙cos30∙2????−????1∙????=0 (5.6)
Σ????????????(????????)=0 : −????????????∙3????+????????∙sin30∙3????−????2∙cos????2∙1,5????+????∙1,5????−M=0 (5.7)
Σ????????????(????????)=0 : ????????????∙3????+????1∙3????+????????∙cos30∙3????=0 (5.8)
Решаем систему из шести уравнений.
Из уравнения (5.3) получим
????????????=????2∙sin????2 = 6∙sin30=3 кН
Из уравнения (5.6) получим
????????=−????1∙????/(cos30∙2????) = −4∙0,8 /(0,866∙2∙0,8)=2,31 Н
Из уравнения (5.8) получим
????????????=(−????1∙3????−????????∙cos30∙3????)/3???? =−????1−????????∙cos30==−4−2,31∙0,866=−6,0005 кН
Из уравнения (5.7) получим
????????????=(????????∙sin30∙3????−????2∙cos????2∙1,5????+????∙1,5????−M)/3а=(2,31∙0,5∙3∙0,8−6∙0,866∙1,5∙0,8+
+3∙1,5∙0,8−5)/3∙0,8=(2,772−6,2352+3,6−5)/2,4=−2,026 кН
Из уравнения (5.5) получим
????????????=−????????????+????????∙sin30−????2∙cos????2+????=2,026+ 2,31∙0,5−6∙0,866+3=0,985 кН
Из уравнения (5.4) получим
????????????=−????????????−????1−Rc’∙cos30= ????????????=6−4−2,31∙0,866= -0,0005 кН
Чтобы убедиться в правильности нахождения опорных реакций, составим проверочные уравнения. Для этого перенесем начало нашей системы координат в точку, где приложен вес плиты.
Σ????????????(????????)=0 :
????????????∙1,5????−????????????∙1,5????+????????∙sin30∙1,5????−М=0,985∙1,5∙0,8+2,026∙1,5∙0,8+2,31∙0,5∙1,5∙0,8−5= =0,0008≈0
Полученная цифра в четвертом знаке после запятой могла получиться потому, что в процессе расчета полученные значения округлялись.
Поэтому можно сделать вывод что проверка сошлась.
Σ????????????(????????)=0 :
−????????????∙1,5????+????????????∙1,5????+????1∙1,5????+????????∙cos30∙1,5????=0,0005∙1,5∙0,8+(−6,0005)∙1,5∙0,8+
+4∙1,5∙0,8+ 2,31∙0,866∙1,5∙0,8=−0,0004≈0
Проверка сошлась.
Определяем величину и направление реакции связи ????????
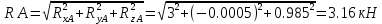
cos????=????????????/????????=3/3,16=−0,949 => ????=18,3°
cos????=????????????/????????=−0,0005/3,16=−0,00015 => ????=90,01°
cos????=????????????/????????=0,985/3,16= 0,312 => ????=71,84°
Определяем величину и направление реакции связи ????B
cos????=????????B/????B=−6,0005/6,33=−0,9479 => ????=161,43°
cos????=????????B/????B=−2,026/6,33= −0,32 => ????=108,67°
Ответ: RA = 3,16 kH, RB = 6,33 kH, RС= 2,31 kH.
6 Задача 6-К: Кинематический анализ плоского механизма
Плоский механизм состоит из стержней 1 – 4 и ползуна В, соединенных друг с другом и с неподвижными опорами O1 и O2 шарнирами (рис. 6.1). Длины стержней равны: l1=0,4 м, l2=1,2 м, l3=1,4 м, l4=0,8 м. Положение механизма определяется углами α, β, γ, φ, θ (см. таблицу 6.1). Точка D находится в середине соответствующего стержня.
Определить величины указанные в таблице 6.1 в столбце «Найти».
Таблица 6.1.
| № вар. | Углы | Дано | Найти | № рис. | |||||||||
| α,° | β,° | γ,° | φ,° | θ,° | ω1, с-1 | ω4, с-1 | υB, м/с | | | ||||
| 18 | 60 | 60 | 60 | 90 | 120 | - | 3 | - | vА, vD, ω3 | 5 | |||
Рисунок 6.1 – Схема плоского механизма
7 Задача 7-К: Сложное движение материальной точки
Условие: Пластина (рисунок 7.1) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в таблице 7.1 (при знаке минус направление ω противоположно показанному на рисунке). Ось вращения OO1, лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка М. Закон ее относительного движения задается уравнением S = AM = f(t), (S – в сантиметрах, t – в секундах), приведенным в таблице 6.1. На всех рисунках точка М показана в положении, при котором S = AM > 0 (при S < 0 точка М находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 c.
Таблица 7.1
| № вар. | ω, c-1 | a, cм | S = AM = f(t), см | № рис. |
| 18 | 4 | 20 | 60∙ (t3−2t2) | 5 |
Рисунок 7.1 – Вращающаяся пластина
Решение. Рассмотрим движение точки М как сложное: относительное движение – поступательное движение точки М вдоль прямой BD, переносное движение – вращательное движение точки М вместе с пластиной вокруг неподвижной оси ОО1. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:
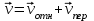, (7.1) 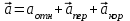, (7.2)или в развернутом виде
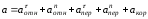. (7.3)Определим положение точки М на прямой .
S = AM= f(t)=60∙ (t3−2t2), (7.4)
Для этого подставим в уравнение (7.4) относительного движения точки время t=1c. подучим
МSt=1 = AM= 60∙ (13−2∙ 12)= −60 cм.
Так как S < 0, то точка М находится по другую сторону от точки А. в области отрицательных значений на отрезке АВ.Выполняем рисунок с необходимыми построениями.
Рассмотрим относительное движение точки М.
Чтобы найти относительную скорость точки М необходимо продифференцировать перемещение по времени. Для этого возьмем первую производную выражения (7.4).
Получим
????отн=????????/????????=(60∙(????3−2????2))′=60∙(3????2−4????),
При t = 1 c получаем
????отн=60∙(3????2−4????)=60∙(3∙12−4∙1)=−60 см/с,
Знак минус говорит о том, что вектор относительной скорости направляем от точки М к точке В. В область отрицательных значений S. Проверить правильность выбора направления скорости можно, подставив в формулу пути другое время, например t = 1,1 с:
???? ????=1,1 =????????=60∙(????3−2????2)=60∙(1,13−2∙1,12)=−65,34 см.
Модуль относительной скорости
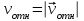=60 см/с.Модуль относительного касательного ускорения
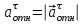, где Рисунок 7.2 – Расчетнаясхема
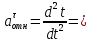(60∙(????3−2????2))′′= 60∙(6????−4).При t = 1 c получаем
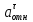=60∙(6????−4)=60∙(6∙1−4)=120 см/с2.Значит
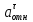=120 см/с2.Вектор
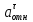направлен в сторону положительных значений, т.к. знаки скорости и ускорения разные, следовательно, относительное движение точки М замедленное.Относительное нормальное ускорение
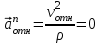, так как траектория относительного движения – прямая линия ( ).Определяем переносную скорость ????e . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO1.
Из точки M опустим перпендикуляр HM на ось OO1.
При переносном движении точка M движется по окружности W (hbceyjr 7/2) радиуса R=HM с центром в точке H.
R=HM = HK + KM = 3a + |AM| sin 30° = 60 + 60·0,5 = 90 см;
Переносное движение:
Переносная скорость точки М перпендикулярна отрезку HМ и равна: