ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 81
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
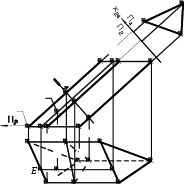
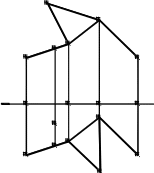
). На развертку призмы нанесена точка К, принадлежащая грани АВВ′А′. Для построения на развертке точки Kиспользована вспомогательная прямая EE′, проходящая через точку Kи парал-лельная ребрам призмы.
14 24 A′ C′
34
A′2 E′2 A′ Σ2B′2C′2
E′ B′
A′
K212A2
E2 B2A111
K′11
22
32C2 A′1
C131
E′1
Σ 1 2 3 1
C
K
C′1 A EB A
A
B1 21 B′1
а) б) Рис. 13.2
Кроме способа нормального сечения, для построения развертки поверхности приз-мы может быть использован способраскатки(частный случай способа нормальных сечений) или способтриангуляции, когда каждая грань призмы делится диагональю на два треугольника [6].
13.2. Построение разверток кривых развертывающихся поверхностей
Напомним, что различают точныеи приближенныеразвертки развертывающихся поверхностей. Точнаяразверткастроится графоаналитическим способом по известным размерам поверхности с использованием ее уравнения. Например, точная развертка бо-ковой поверхности прямого кругового цилиндра высотой Hи радиусом основания r имеет форму прямоугольника с размерами сторон Hи 2πr.
Приближеннаяразверткастроится графическим способом с использованием чер-тежа поверхности. Чтобы построить приближенную развертку какой-либо разверты-вающейся поверхности, надо ее заменить (аппроксимировать) многогранной поверхно-стью. Точную развертку этой многогранной поверхности принимают за приближенную развертку данной развертывающейся поверхности.
13.2.1. Точная развертка поверхностипрямого кругового конуса
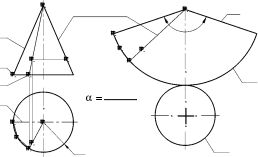
Точная развертка поверхности прямого кругового конуса, образующая которого равна lи радиус основания r(рис. 13.3, а), имеет форму кругового сектора с радиусом l и центральным углом α=360°
r/l(рис. 13.3, б).
Задача. НаповерхностиконусаотмеченаточкаK.ПостроитьточкуKнараз-вертке конуса.
Через точку Kна поверхности конуса проведем его образующую S-3(см. рис. 13.3, а). Найдем положение образующей S-3на развертке конуса. Для этого дугу 1-3круго-вого основания конуса заменяем ломаной линией 123. Участки этой ломаной линии от-кладываем от точки 1на развертке конуса (вдоль дуги кругового сектора). Получаем на развертке точку 3, через которую проходит образующая S-3.
S2 |SK|=|S2K′2| S l l21 α
12 K2 K′2 23 K
32
l1
11 S1
2πr3600 r
l
2131K1 r 2πr
а) б) Рис. 13.3
Расстояние SKот вершины Sдо искомой точки Kопределено на рис. 13.3, аспосо-бом вращения вокруг проецирующей прямой: мысленно вращаем отрезок SKвокруг горизонтально-проецирующей оси конуса (см. п. 5.5). Вращение отрезка заканчивается в тот момент, когда он займет положение фронтали (совместится с фронтальной проек-цией очерковой образующей конуса). Фронтальная проекция S2K2′повернутого отрезка определяет натуральную величину отрезка SK. Расстояние SKна развертке равно рас-стоянию S2K2′ на фронтальной проекции конуса.
Заметим, что построение точки Kна развертке выполнено приближенным графиче-ским способом: дуга 1-3кругового основания конуса заменена ломаной линией 123. Хотя развертка конуса была построена точно, но точка Kна развертке найдена прибли-женно, поэтому решение задачи в целом следует считать приближенным.
13.2.2. Точная развертка поверхности усеченного кругового цилиндра
714 34
1 5
74
54 22=(42)
12=(52)
62=(82)
32 3 4 синусоида
1 2 5 1
6 8
72 Σ2
7
61 51 41 2πr
71 31 r
81 21 11
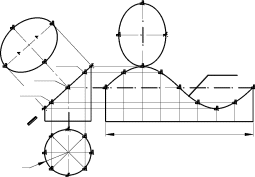
Рис. 13.4
На рис. 13.4 представлена развертка косорассеченного цилиндра. Верхняя часть ци-линдра вращения “срезана” наклонной плоскостью Σ. Фигура косого сечения представ-ляет собой эллипс. На развертке цилиндра этот эллипс “пере-
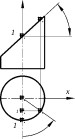
ходит” в синусоиду, в чем можно убедиться следующим обра- y
зом. A2 βПусть по наклонному сечению цилиндра (эллипсу) дви-
жется точка A (рис. 13.5). Координата xAточки Aравна отрезку 2 A1P1и вычисляется по формуле xArsin, где r– радиус
A
цилиндра. Высота zAточки A, отсчитываемая от уровня точки 1, определяется формулой zAxAtg. Подставляя во вторую формулу вместо координаты xее выражение из первой фор-мулы, получаем: zAksin, где krtg. Таким образом,
высота точки, движущейся по линии наклонного сечения ци- P A1
линдра, пропорциональна синусу угла поворота φточки A.
При изменении угла φот 0°до 360°точка A“пробегает” всю 1 φлинию сечения (эллипс), а на развертке цилиндра получается
полная волна синусоиды. Рис. 13.5
13.2.3. Приближенная развертка поверхностипрямого кругового конуса
Напомним, что для построения приближенной развертки развертывающейся по-верхности надо ее аппроксимировать (приближенно заменить) многогранной поверхно-стью. Заменим поверхность конуса поверхностью вписанной в него пирамиды.
На рис. 13.6, апоказана правильная 12-угольная пирамида, вписанная в прямой круговой конус. Основание пирамиды – правильный 12-угольник, вписанный в круго-вое основание конуса. Поверхность конуса приближенно заменена двенадцатью одина-ковыми треугольниками (гранями пирамиды, вписанной в конус). Это геометрическое
действие (аппроксимация криволинейной поверхности сеткой треугольников) называ-ют триангуляцией.
14 24 A′ C′34
A′2 E′2 A′ Σ2B′2C′2
E′ B′
A′
K212A2
E2 B2A111 K′1122
32C2 A′1
C131
E′1Σ 1 2 3 1
C
K
C′1 A EB A
A
B1 21 B′1
а) б) Рис. 13.2
Кроме способа нормального сечения, для построения развертки поверхности приз-мы может быть использован способраскатки(частный случай способа нормальных сечений) или способтриангуляции, когда каждая грань призмы делится диагональю на два треугольника [6].
13.2. Построение разверток кривых развертывающихся поверхностей
Напомним, что различают точныеи приближенныеразвертки развертывающихся поверхностей. Точнаяразверткастроится графоаналитическим способом по известным размерам поверхности с использованием ее уравнения. Например, точная развертка бо-ковой поверхности прямого кругового цилиндра высотой Hи радиусом основания r имеет форму прямоугольника с размерами сторон Hи 2πr.
Приближеннаяразверткастроится графическим способом с использованием чер-тежа поверхности. Чтобы построить приближенную развертку какой-либо разверты-вающейся поверхности, надо ее заменить (аппроксимировать) многогранной поверхно-стью. Точную развертку этой многогранной поверхности принимают за приближенную развертку данной развертывающейся поверхности.
13.2.1. Точная развертка поверхностипрямого кругового конуса
Точная развертка поверхности прямого кругового конуса, образующая которого равна lи радиус основания r(рис. 13.3, а), имеет форму кругового сектора с радиусом l и центральным углом α=360°
r/l(рис. 13.3, б).
Задача. НаповерхностиконусаотмеченаточкаK.ПостроитьточкуKнараз-вертке конуса.
Через точку Kна поверхности конуса проведем его образующую S-3(см. рис. 13.3, а). Найдем положение образующей S-3на развертке конуса. Для этого дугу 1-3круго-вого основания конуса заменяем ломаной линией 123. Участки этой ломаной линии от-кладываем от точки 1на развертке конуса (вдоль дуги кругового сектора). Получаем на развертке точку 3, через которую проходит образующая S-3.
S2 |SK|=|S2K′2| S l l21 α12 K2 K′2 23 K
32
l1
11 S1
2πr3600 r
l
2131K1 r 2πr
а) б) Рис. 13.3
Расстояние SKот вершины Sдо искомой точки Kопределено на рис. 13.3, аспосо-бом вращения вокруг проецирующей прямой: мысленно вращаем отрезок SKвокруг горизонтально-проецирующей оси конуса (см. п. 5.5). Вращение отрезка заканчивается в тот момент, когда он займет положение фронтали (совместится с фронтальной проек-цией очерковой образующей конуса). Фронтальная проекция S2K2′повернутого отрезка определяет натуральную величину отрезка SK. Расстояние SKна развертке равно рас-стоянию S2K2′ на фронтальной проекции конуса.
Заметим, что построение точки Kна развертке выполнено приближенным графиче-ским способом: дуга 1-3кругового основания конуса заменена ломаной линией 123. Хотя развертка конуса была построена точно, но точка Kна развертке найдена прибли-женно, поэтому решение задачи в целом следует считать приближенным.
13.2.2. Точная развертка поверхности усеченного кругового цилиндра
714 341 5
74
54 22=(42)
12=(52)
62=(82)
32 3 4 синусоида
1 2 5 1
6 8
72 Σ2
7
61 51 41 2πr
71 31 r
81 21 11
Рис. 13.4
На рис. 13.4 представлена развертка косорассеченного цилиндра. Верхняя часть ци-линдра вращения “срезана” наклонной плоскостью Σ. Фигура косого сечения представ-ляет собой эллипс. На развертке цилиндра этот эллипс “пере-ходит” в синусоиду, в чем можно убедиться следующим обра- y
зом. A2 βПусть по наклонному сечению цилиндра (эллипсу) дви-
жется точка A (рис. 13.5). Координата xAточки Aравна отрезку 2 A1P1и вычисляется по формуле xArsin, где r– радиус
A
цилиндра. Высота zAточки A, отсчитываемая от уровня точки 1, определяется формулой zAxAtg. Подставляя во вторую формулу вместо координаты xее выражение из первой фор-мулы, получаем: zAksin, где krtg. Таким образом,
высота точки, движущейся по линии наклонного сечения ци- P A1
линдра, пропорциональна синусу угла поворота φточки A.
При изменении угла φот 0°до 360°точка A“пробегает” всю 1 φлинию сечения (эллипс), а на развертке цилиндра получается
полная волна синусоиды. Рис. 13.5
13.2.3. Приближенная развертка поверхностипрямого кругового конуса
Напомним, что для построения приближенной развертки развертывающейся по-верхности надо ее аппроксимировать (приближенно заменить) многогранной поверхно-стью. Заменим поверхность конуса поверхностью вписанной в него пирамиды.
На рис. 13.6, апоказана правильная 12-угольная пирамида, вписанная в прямой круговой конус. Основание пирамиды – правильный 12-угольник, вписанный в круго-вое основание конуса. Поверхность конуса приближенно заменена двенадцатью одина-ковыми треугольниками (гранями пирамиды, вписанной в конус). Это геометрическое
действие (аппроксимация криволинейной поверхности сеткой треугольников) называ-ют триангуляцией.