Файл: Учебнометодический комплекс по дисциплине электрооборудование фармацевтического производства для специальности 5В074800 Технология фармацевтического производства.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 210

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Министерство образования и науки Республики Казахстан

Караганда

Тема 7 Импульсные и цифровые устройства Импульсная техника – раздел электроники, предметом которого является разработка теоретических основ, практических методов и технических средств генерирования, преобразования и измерения параметров электрических импульсов, а также исследование импульсных процессов в электрических цепях. Наиболее часто в импульсных электронных устройствах используются импульсы прямоугольной (рис. 34,а), трапецеидальной (рис. 34,б), треугольной (рисунок 34,в) и экспоненциальной (рис. 34,г) формы. Импульсы, формы которых приведены на рис. 34,а…г, являются идеализированными. Форма реальных импульсов не является геометрически правильной из-за нелинейности характеристик полупроводниковых приборов и влияния реактивных сопротивлений в схемах. Поэтому реальные прямоугольные импульсы, наиболее часто используемые в практических импульсных схемах, имеют форму, приведенную на рис. 34,д.Участки быстрого нарастания и спада напряжения или тока называются фронтом и срезом импульса, а интервал, на котором напряжение или ток изменяются сравнительно медленно,- вершиной импульса.Активные длительности фронта τфа и среза τса определяются между уровнями 0,1Um и 0,9Um, где Um – амплитуда импульса. Активная длительность вершины τа оценивается на уровне 0,5Um. Импульс, показанный на рис. 34,д, имеет обратный выброс с амплитудой Um обр. Кроме того, на его вершину наложены затухающие синусоидальные колебания, который, как правило, возникают из-за наличия в схеме паразитных колебательных цепей, образованных распределенными индуктивностями и емкостями. Рисунок 34Упрощенная форма реального прямоугольного импульса показана на рис. 34,е. Спрямленные отрезки ab, bc, cd отображают соответственно фронт, вершину и срез импульса, а отрезки de и ef – нарастание и спад обратного импульса. Скорость нарастания напряжения или тока на рис. 34,е характеризуется крутизной фронта импульса, а убывание напряжения или тока на вершине относительным снижением.Одним из важнейших показателей импульсных сигналов является длительность импульсов. Помимо указанного параметра τа, определяющего активную длительность вершины на уровне 0,5Um, длительность импульса характеризует время tи, определяемое либо на уровне 0,1Um, либо по основанию импульса (рис. 34,е).К основным параметрам импульсов относится период повторения импульсов Т – интервал времени между началом двух соседних однополярных импульсов. Величину, обратную периоду повторения, называют частотой следования импульсов ν. Часть периода Т занимает пауза tп – отрезок времени между окончанием и началом двух соседних импульсов tп = T – tи.Отношение длительности импульса к периоду повторения называется коэффициентом заполненияВеличина, обратная коэффициенту заполнения, называется скважностью импульсовКачество работы импульсных устройств во многом определяется временем восстановления импульса tвос (рис. 34,е). Чем меньше tвос, тем надежнее работает схема, тем выше ее быстродействие.Мультивибраторы. Одним из наиболее распространенных генераторов импульсов прямоугольной формы является мультивибратор, представляющий собой двухкаскадный резистивный усилитель с глубокой положительной обратной связью. Одна из наиболее простых и типичных схем мультивибратора приведена на рис. 35. Элементы схемы подобраны так, чтобы обеспечить идентичность каждого из усилительных каскадов, собранных на однотипных транзисторах VТ1, VT2. При R1 = R4, R2 = R3, C1 = C2 и одинаковых параметрах транзистора мультивибратор называется симметричным. Рисунок 35На рис. 36 приведены временные диаграммы токов, протекающих в транзисторах, и напряжений на коллекторах и базах транзисторов. Исходный момент t0 соответствует тому случаю, когда транзистор VT1 заперт, а транзистор VT2 открыт. Моменты t1, t2, t3 соответствуют переключению схемы. Рисунок 36Базовые логические элементы. Применение двоичной системы счисления в цифровой электронике обеспечивает более высокую скорость выполнения операций и более высокую надежность электронной аппаратуры, т.к. элементной базой для ее построения служат элементы с двумя устойчивыми состояниями. Для описания алгоритмов работы цифровых устройств используется соответствующий математический аппарат, получивший название булевой алгебры или алгебры логики. Каждую конкретную комбинацию значений аргументов называют набором. При n аргументах существует 2n наборов. Для краткости набор записывается в виде двоичного числа, цифрами которого являются значения переменных, расположенных в определенном порядке. Двоичное число, представляющее набор, называется номером набора и обозначается α.. При n аргументах совокупность всех значений функции на 2n наборах содержит 2n нулей и единиц. Каждой функции соответствует своя комбинация этих 2n значений. Общее количество всех возможных функций n аргументов определяется числом .Логические функции одной переменной приведены в таблице 1,Таблица 1

Тематика рефератов:

Тема 2 Цепи при гармоническом воздействии

Электрические цепи однофазного переменного тока.


Основные формулы:

(18)

Рисунок 3
. (19)

. (20)

. (21)

. (22)

Расчет электрических цепей однофазного переменного тока.


Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление (входная проводимость) вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.

Резонанс в цепи с последовательно соединенными элементами (резонанс напряжений).

Для приводимой цепи в зависимости от соотношения величин и возможны три различных случая.

1. В цепи преобладает индуктивность, следовательно, этому режиму соответствует векторная диаграмма.

2. В цепи преобладает емкость. Этот случай отражает векторная диаграмма.

3. В цепи имеет место равенство реактивных сопротивлений - случай резонанса напряжений.

Условие резонанса напряжений.

При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания.

Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.

Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае, и условие резонанса выполняется для эквивалентных значений L
Э и CЭ.

Как показывает анализ, уравнения режима резонанса можно добиться путем изменения параметров L и C, а также частоты.

Резонансными кривыми называются зависимости тока и напряжения от частоты.

Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению, и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания.

Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью.

Резонанс в цепи с параллельно соединенными элементами (резонанс токов).

Для приводимой цепи в зависимости от соотношения величин, как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.

В цепи преобладает индуктивность, следовательно, этому режиму соответствует векторная диаграмма.

В цепи преобладает емкость, значит, этот случай иллюстрирует векторная диаграмма.

В цепи имеет место равенство реактивных сопротивлений - случай резонанса токов.

Условие резонанса токов.

При резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности, при отсутствии в цепи резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.

Основная литература: [1, 3];

Дополнительная литература: [9, 11].
Тема 3 Методы анализа сложных электрических цепей

Расчет сложных электрических цепей постоянного тока.


Метод узловых и контурных уравнений. Метод контурных токов.

а) Метод наложения (суперпозиции).

Метод наложения может быть применен ко всем электрическим процессам, описываемым линейными уравнениями.

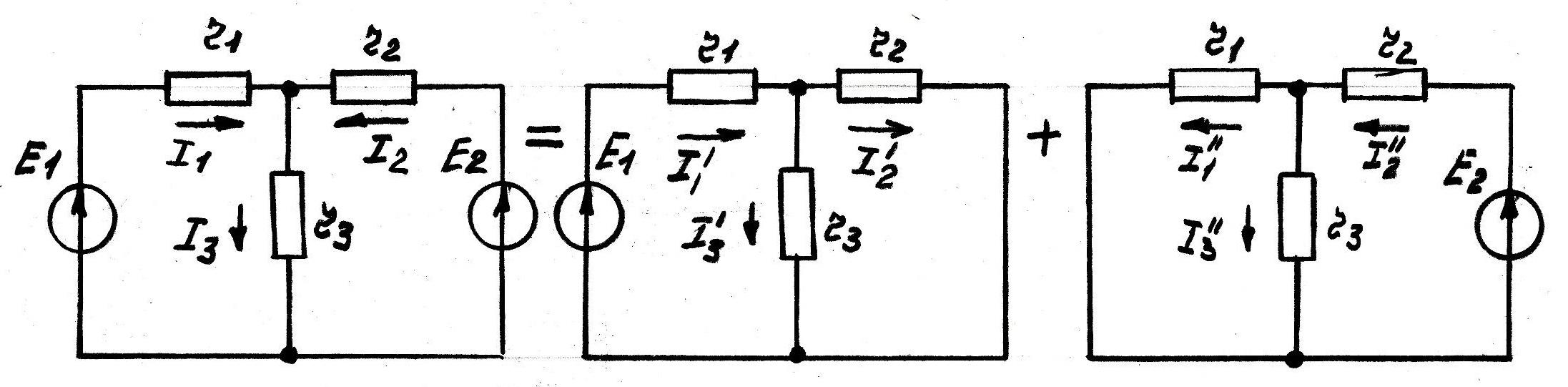
Рисунок 4
Суть метода заключается в определении токов при действии источников ЭДС раздельно, а затем алгебраическом сложении полученных значений. После исключения Е2 получается смешанное соединение резистивных элементов. Тогда

;
; .

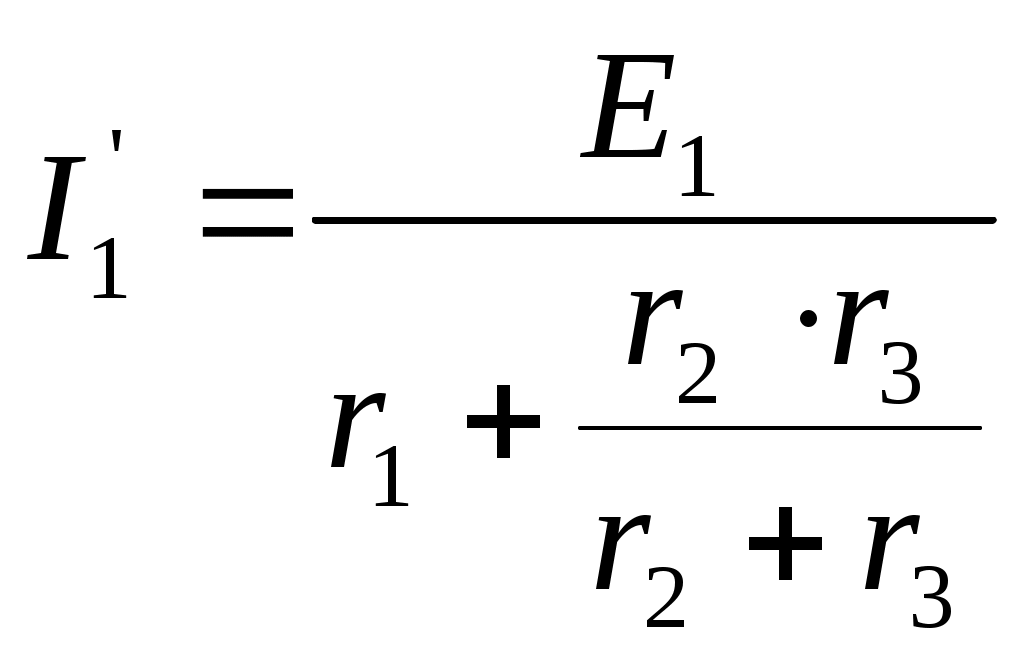Затем исключается Е1 и рассчитываются токи

; ; .

По методу наложения

; ; ;

Если у источников имеются внутренние сопротивления, то при расчете источники заменяются соответствующим резистивными элементами.

в) Метод контурных токов.

Метод может быть применен для расчета любой линейной цепи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Кирхгофа.

Независимые контуры выбираются для сложной электрической цепи так же, как и при составлении уравнений по второму закону Кирхгофа (I, II, III). Затем в каждом из контуров произвольно выбирается положительное направление контурного тока (I11; I22; I33). Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих токов.

Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС (ЕКК), т.е.

; ; .

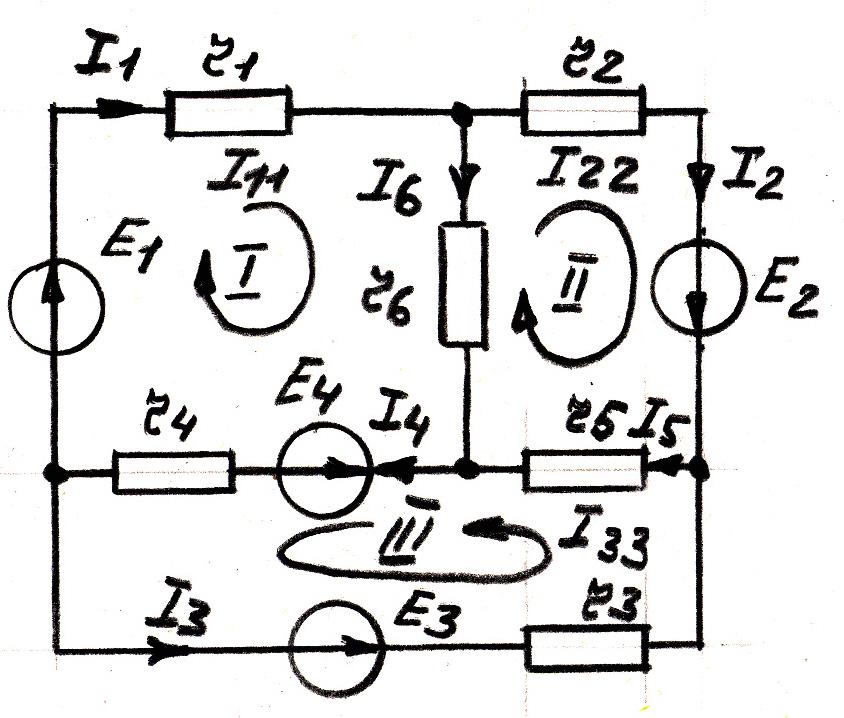
Рисунок 5
Арифметическая сумма сопротивлений всех резистивных элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением (rКК).

; ; .

Арифметическая сумма сопротивлений резистивных элементов, находящихся в общих ветвях двух контуров m и l называется общим сопротивлением этих контуров (r
ml = rlm).

; ; .

Для контурных токов должен выполняться второй закон Кирхгофа. Тогда







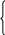
Решение полученной системы уравнений может быть записано для контурных токов в общей форме с введением определителей



В рассматриваемом примере







Определитель системы





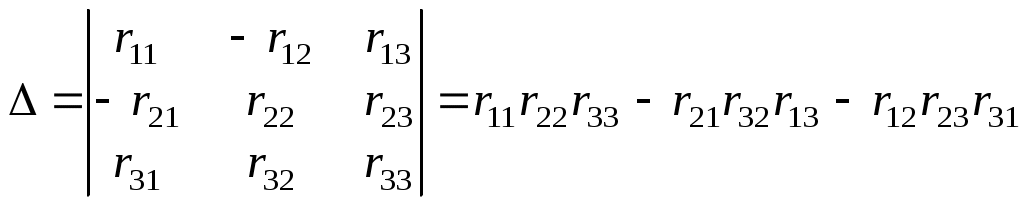
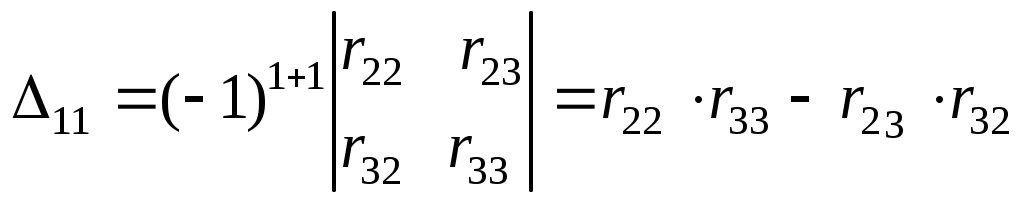
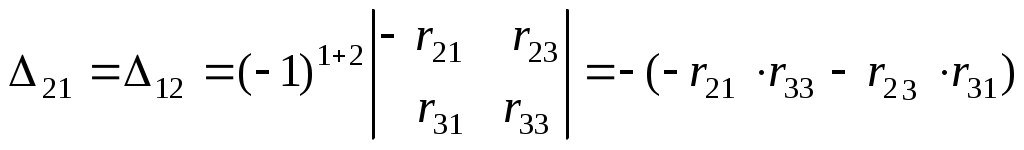
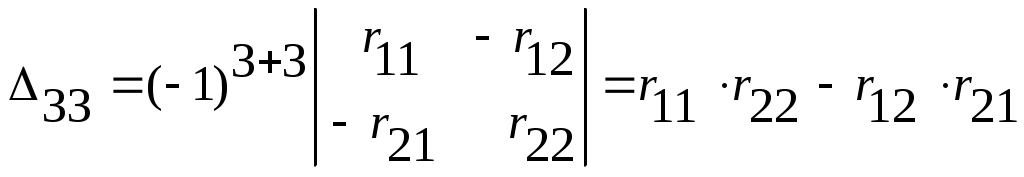- алгебраические дополнения, получаемые из определителя Δ посредством вычеркивания К-й строки и Р-го столбца и умножением полученного определителя на (-1)К+Р.





.







.

.

Вычислив значение контурных токов
, определим по первому закону Кирхгофа токи во всех ветвях цепи:

, , , , ,

Метод контурных токов применим и для расчета цепи, если ее схема содержит источники тока. В этом случае ток каждого контура, который содержит источник тока, известен и равен току источника. Поэтому для таких контуров составлять уравнения не нужно.

Электрические цепи трехфазного тока.


Три синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые по фазе на , образуют трёхфазную симметричную систему. Аналогично получаются трёхфазные системы напряжений и токов.

В настоящее время трёхфазные системы получили широкое распространение, что объясняется главным образом следующими причинами: 1) при одинаковых условиях питание трёхфазным током позволяет получить значительную экономию материала проводов по сравнению с тремя однофазными линиями; 2) при прочих равных условиях трёхфазный генератор дешевле, легче и экономичнее, чем три однофазных генератора такой же общей мощности; то же относится к трёхфазным двигателям и трансформаторам; 3) трёхфазная система токов позволяет получить вращающееся магнитное поле с помощью трёх неподвижных катушек, что существенно упрощает производство и эксплуатацию трехфазных двигателей; при равномерной нагрузке трёхфазный генератор создаёт на валу приводного двигателя постоянный момент в отличие от однофазного генератора, у которого мощность и момент на валу пульсируют с двойной частотой.

При симметричной нагрузке, когда все три нагрузочных сопротивления равны по значению и имеют одинаковый характер, синусоиды напряжений и токов изображаются графиками, аналогичными графику ЭДС. При этом начальные фазы токов определяются характером нагрузки, токи

Смотрите также файлы