Файл: Умноженной на множитель в форме показательной функции W.docx

8. Линейные дискретные системы (ЛДС) с постоянными параметрами. Понятие о разностном уравнении. Порядок разностного уравнения. Связь разностного уравнения и структуры ЛДС, пример. Рекурсивные и нерекурсивные ЛДС, структурные схемы. Понятие КИХ и БИХ систем. Связь КИХ и БИХ систем с рекурсивными и нерекурсивными системами. Устойчивость КИХ и БИХ систем.

Рекурсивные и нерекурсивные линейные дискретными системы

Линейная дискретная система называется рекурсивной, если хотя бы один из коэффициентов_k разностного уравнения (1.15) не равен нулю:

хотя бы для одного из значений k.

Порядкомрекурсивной ЛДС называют порядок РУ (1.15), т. е. .

Согласно (1.15) реакция y(n)рекурсивнойЛДС в каждый момент времениnопределяется:

• 
  текущим отсчетом воздействия x(n);
  
• 
  предысторией воздействия  ;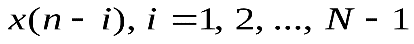
  
• 
  предысторией реакции  .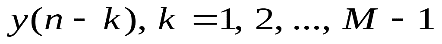
  

Примеры разностных уравнений рекурсивной ЛДС:

• 
  первогопорядка
  

; (1.16)

• 
  второгопорядка
  

.(1.17)

Линейная дискретная система называется нерекурсивной, если все коэффициенты разностного уравнения (1.15) равны нулю:

,  .

Для нерекурсивной ЛДС разностные уравнения (1.14)–(1.15) принимают вид соответственно

---

; (1.18)

. (1.19)

Порядокнерекурсивной ЛДС равен .

Согласно РУ (1.19) реакция  нерекурсивнойЛДС в каждый момент времениnопределяется:

• 
  текущим отсчетом воздействия  ;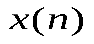
  
• 
  предысторией воздействия  .
  

Пример РУ нерекурсивной ЛДС второго порядка:

. (1.20)

---

1.3.4. Ких- и бих-системы

Рассмотрим особенности импульсныххарактеристикрекурсивных и нерекурсивных ЛДС. С этой целью приведем примеры вычисления ИХ по заданному разностному уравнению, решая его методом прямой подстановки при нулевых начальных условиях.

Пример 1.3.Вычислить импульсную характеристикунерекурсивнойЛДС второго порядка, соотношение вход/выход которой описывается разностным уравнением (1.20):

.

Решение.Согласно определению ИХ – этореакцияна цифровой единичный импульс (рис. 1.6), поэтому, выполнив замену

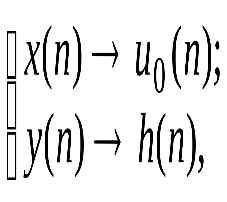 (1.21)

перепишем РУ в виде



и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях (см. п. 1.3.2):

;

;

;

;

при  .

Распространяя полученные результаты на ИХ нерекурсивной ЛДС произвольного порядка, можно сделать следующие выводы:

- импульсная характеристика нерекурсивной ЛДС имеет конечную длительность;

- значения отсчетов ИХ равны коэффициентам разностного уравнения

, при  .

Поэтому нерекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ-системами).

Пример 1.4.

---

Вычислить импульсную характеристикурекурсивнойЛДС первого порядка, соотношение вход/выход которой описывается разностным уравнением

.

Решение.Выполнив замену (1.21), перепишем РУ в виде



и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях:

;

;

;

.

Вычисления можно продолжать бесконечно по формуле

, 

Распространяя полученные результаты на ИХ рекурсивнойЛДС произвольного порядка, можно сделать вывод: импульсная характеристикарекурсивнойЛДС имеетбесконечнуюдлительность.

Поэтому рекурсивные ЛДС называют системами с бесконечной импульсной характеристикой (БИХ-системами).

Устойчивость линейных дискретных систем

ЛДС называется устойчивой, если при ограниченном воздействии

,

где  – любое, сколь угодно большое положительное число, не равное бесконечности, и произвольных, но ограниченных начальных условиях реакция также ограничена

,

где  – любое сколь угодно большое положительное число, не равное бесконечности.

Оценка устойчивости по импульсной характеристике

---

Существуют два критерияустойчивости ЛДС. Один из них позволяет оценить устойчивость ЛДС по ее импульсной характеристике во временной области, другой – поz-изображению этой характеристики вz-области (см. п. 1.4). Выбор критерия зависит от удобства его практического использования.

Критерий, позволяющей оценить устойчивость ЛДС по ее импульсной характеристике, формулируется следующим образом: для того чтобы ЛДС была устойчива, необходимо и достаточно выполнения условия абсолютной сходимости ряда

. (1.21а)

Данный критерий устойчивости свидетельствует о том, что нерекурсивныеЛДС (КИХ-системы)всегдаустойчивы, поскольку их импульсная характеристика конечна.

Прежде чем делать вывод об устойчивости рекурсивных ЛДС, рассмотрим простой пример.

Пример 1.5. Определить, устойчива ли рекурсивная ЛДС, импульсная характеристика которой описывается дискретной экспонентой (1.6)



Решение. Подставив данную ИХ в правую часть критерия (1.21а), получим ряд

,

представляющий собой сумму бесконечной геометрической прогрессии

,  .

Как известно, сумма такого ряда в области сходимости, т. е. при  , имеет конечный предел, равный

.

В этом случае импульсная характеристика представляет собой затухающуюэкспоненту (см. рис. 1.3), а ЛДС согласно критерию (1.21а) является устойчивой.

Вне указанной области, т. е. при 

---