Файл: Умноженной на множитель в форме показательной функции W.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 452
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
, сумма бесконечной геометрической прогрессии не имеет конечного предела, ряд является расходящимся
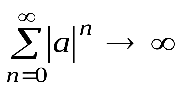 ,
,
а ЛДС по критерию (1.21а) – неустойчивой.
В общем случае относительно устойчивости БИХ-систем можно сделать следующие выводы:
- рекурсивные ЛДС (БИХ-системы) требуют проверки на устойчивость,
- импульсная характеристика устойчивой ЛДС имеет характер затухающей функции времени.
9. Линейные дискретные системы (ЛДС) с постоянными параметрами. Понятие о передаточной функции ЛДС. Связь передаточной функции ЛДС с ее структурой, примеры. Нули и полюса передаточной функции линейной дискретной системы, определение. Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции. Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия.
* Систему называют линейной, если она удовлетворяет принципам суперпозиции (реакция на сумму воздействий равна сумме реакций на данные воздействия) и однородности (воздействию, умноженному на весовой коэффициент, соответствует реакция, умноженная на тот коэффициент).
* Систему называют дискретной, если она преобразует дискретное воздействие x(n) в дискретную реакцию y(n), где n – порядковый номер отсчёта (индекс элемента входной или выходной числовой последовательности), отмеряющий момент времени в интервалах дискретизации T.
Передаточная функция ЛДС - отношение z-изображения реакции к z-изображению воздействия при нулевых начальных условиях (ННУ):
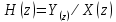
Соотношение можно получить, выполнив z-преобразование разностного уравнения (РУ):
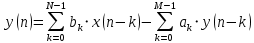
ak, bk - вещественные коэффициенты
k – значения задержек воздействия и реакции
(N - 1), (M - 1) – константы, определяющие максимальные задержки
Связь передаточной функции ЛДС с ее структурой, примеры.
Структура ЛДС отображает алгоритм вычисления реакции по РУ и определяется видом передаточной функции.
Для рекурсивных звеньев 2-ого порядка с передаточной функцией:
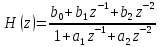
и разностным уравнением
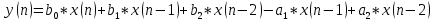
поддерживаются следующие структуры
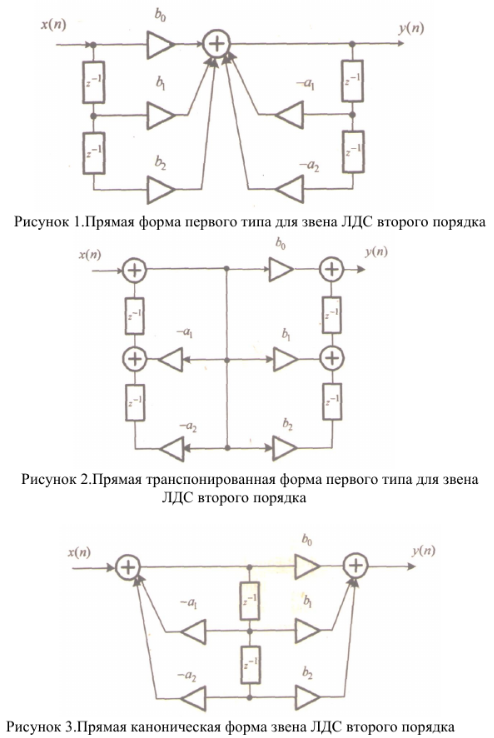
* Прямая форма первого типа – Direct-Form Ⅰ (Рисунок 1)
* Прямая транспонированная - Direct-Form Ⅰ Transposed (Рисунок 2)
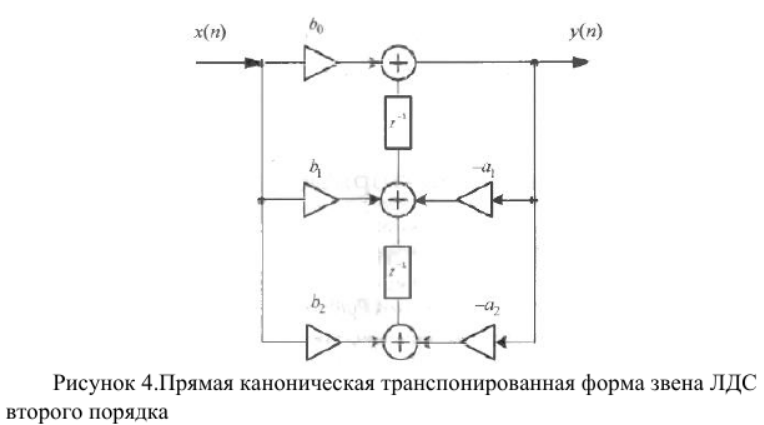
* Прямая каноническая - Direct-Form Ⅱ (Рисунок 3)
*Прямая каноническая транспонированная - Direct-Form Ⅱ Transposed (Рисунок 4)
Нули и полюса передаточной функции линейной дискретной системы, определение.
Нули – значения z на комплексной плоскости при которых функция равна нулю.
Полюса (особые точки) – значения z при которых знаменатель функции равен нулю.
Карта нулей и полюсов – z плоскость с нанесённой единичной окружностью и символически изображёнными нулями и полюсами.
Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции.
По карте нулей и полюсов можно сделать вывод об устойчивости ЛДС: полюсы располагаются внутри единичного круга с центром в начале координат.
Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия.





ЛДС с постоянными параметрами (из его электронной доски)
Делятся на:
- устойчивые
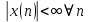
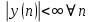
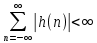
-не устойчивые
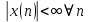
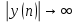
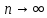
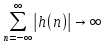
Предварительно можно оценить по графику
Если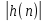 убывающая, то
убывающая, то 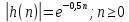
Если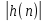 возрастающая, то
возрастающая, то 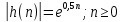
Также ЛДС с постоянными параметрами делятся на:
-Физически реализуемая
Не нарушает принцип причинности т.е. реакция на выходе цепи не опережает воздействие.
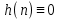
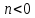
-Физически нереализуемая
Контр. пример
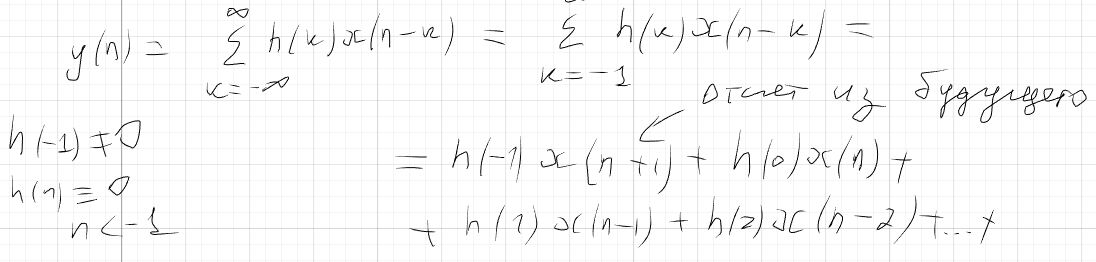
y(n) – отчет реакции в данный момент времени
2. (материал из методички) Основной характеристикой ЛДС в частотной области является частотная характеристика (ЧХ)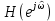 – Фурье-изображение ИХ h(n) :
– Фурье-изображение ИХ h(n) :
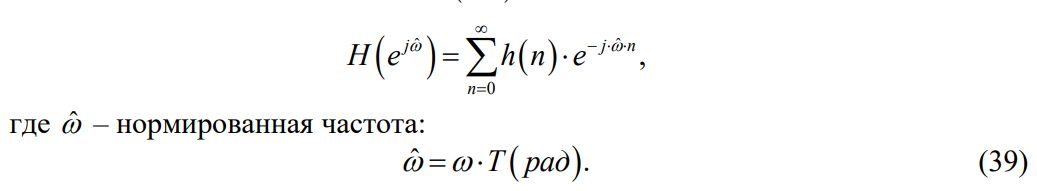
Частотная характеристика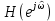 связана с передаточной функцией H z соотношением:
связана с передаточной функцией H z соотношением:
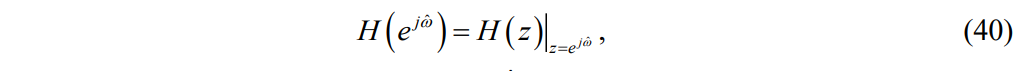
что позволяет путем подстановки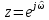 в (32) получить ее в виде:
в (32) получить ее в виде:
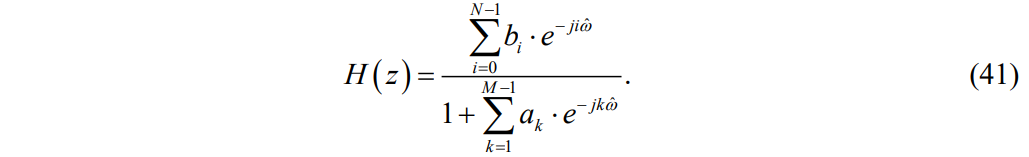
Про формулу 32.
Передаточной функцией ЛДС называют отношение z-изображения реакции к z-изображению воздействия при ННУ:
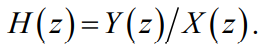
Данное отношение легко получить, выполнив Z-преобразование РУ (30). Передаточная функция рекурсивной ЛДС имеет вид дробно-рациональной функции:
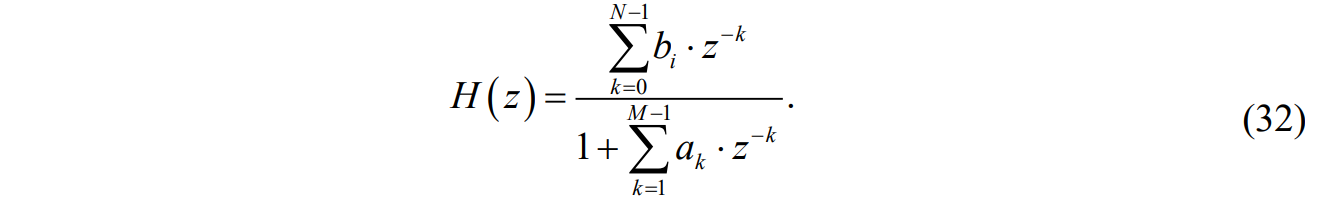
Показатель степени z-k соответствует задержкам воздействия b задержкам реакции; коэффициенты ak передаточной функции и РУ (30) имеют противоположные знаки.Соотношение вход/выход ЛДС, однозначно связанное с его основной характеристикой в z-области – передаточной функцией, имеет вид линейного математического преобразования в виде разностного уравнения (РУ):
Про формулу 30 из его электронной доски.
Разностное уравнение
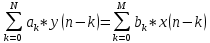
x(n) – воздействие
y(n) – реакция
k – значения задержек воздействия и реакции
ak, bk – вещественные коэффициенты (параметры) РУ
N, M – константы, определяющие максимальные задержки
R = max(N, M) – порядок ЛДС (порядок фильтра)
РУ задаёт алгоритм для нахождения y(n)
3. (материал из методички) Амплитудно-частотная характеристика (АЧХ) отображает частотную зависимость отношения амплитуды реакции к амплитуде гармонического воздействия в установившемся режиме.
Фазочастотная характеристика (ФЧХ) отображает частотную зависимость разности фаз реакции и гармонического воздействия в установившемся режиме.
АЧХ и ФЧХ – периодические функции с периодом 2π в шкале частот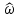 или fд в шкале частот f (Гц).
или fд в шкале частот f (Гц).
АЧХ – четная, а ФЧХ – нечетная функция частоты.
АЧХ и ФЧХ рассчитываются в основной полосе частот [0; π] в шкале частот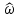 или [0; fд
или [0; fд
/2 ] в шкале частот f (Гц).
а ЛДС по критерию (1.21а) – неустойчивой.
В общем случае относительно устойчивости БИХ-систем можно сделать следующие выводы:
- рекурсивные ЛДС (БИХ-системы) требуют проверки на устойчивость,
- импульсная характеристика устойчивой ЛДС имеет характер затухающей функции времени.
9. Линейные дискретные системы (ЛДС) с постоянными параметрами. Понятие о передаточной функции ЛДС. Связь передаточной функции ЛДС с ее структурой, примеры. Нули и полюса передаточной функции линейной дискретной системы, определение. Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции. Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия.
* Систему называют линейной, если она удовлетворяет принципам суперпозиции (реакция на сумму воздействий равна сумме реакций на данные воздействия) и однородности (воздействию, умноженному на весовой коэффициент, соответствует реакция, умноженная на тот коэффициент).
* Систему называют дискретной, если она преобразует дискретное воздействие x(n) в дискретную реакцию y(n), где n – порядковый номер отсчёта (индекс элемента входной или выходной числовой последовательности), отмеряющий момент времени в интервалах дискретизации T.
Передаточная функция ЛДС - отношение z-изображения реакции к z-изображению воздействия при нулевых начальных условиях (ННУ):
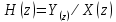
Соотношение можно получить, выполнив z-преобразование разностного уравнения (РУ):
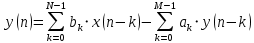
ak, bk - вещественные коэффициенты
k – значения задержек воздействия и реакции
(N - 1), (M - 1) – константы, определяющие максимальные задержки
Связь передаточной функции ЛДС с ее структурой, примеры.
Структура ЛДС отображает алгоритм вычисления реакции по РУ и определяется видом передаточной функции.
Для рекурсивных звеньев 2-ого порядка с передаточной функцией:
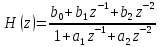
и разностным уравнением
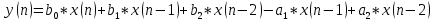
поддерживаются следующие структуры
* Прямая форма первого типа – Direct-Form Ⅰ (Рисунок 1)
* Прямая транспонированная - Direct-Form Ⅰ Transposed (Рисунок 2)
* Прямая каноническая - Direct-Form Ⅱ (Рисунок 3)
*Прямая каноническая транспонированная - Direct-Form Ⅱ Transposed (Рисунок 4)


Нули и полюса передаточной функции линейной дискретной системы, определение.
Нули – значения z на комплексной плоскости при которых функция равна нулю.
Полюса (особые точки) – значения z при которых знаменатель функции равен нулю.
Карта нулей и полюсов – z плоскость с нанесённой единичной окружностью и символически изображёнными нулями и полюсами.
Условие устойчивости ЛДС, выраженное через требование к полюсам ее передаточной функции.
По карте нулей и полюсов можно сделать вывод об устойчивости ЛДС: полюсы располагаются внутри единичного круга с центром в начале координат.
Передаточные функции рекурсивных и нерекурсивных ЛДС, отличия.






- Линейные дискретные системы (ЛДС) с постоянными параметрами. Частотная характеристика линейной дискретной системы и ее связь с передаточной функцией ЛДС. Амплитудно- и фазочастотная характеристики ЛДС. Связь нулей и полюсов передаточной функции с положениями локальных минимумов и максимумов амплитудно-частотной характеристики на частотной оси.
ЛДС с постоянными параметрами (из его электронной доски)
Делятся на:
- устойчивые
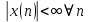
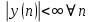
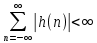
-не устойчивые
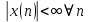
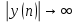
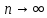
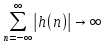
Предварительно можно оценить по графику
Если
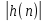 убывающая, то
убывающая, то 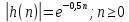
Если
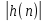 возрастающая, то
возрастающая, то 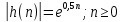
Также ЛДС с постоянными параметрами делятся на:
-Физически реализуемая
Не нарушает принцип причинности т.е. реакция на выходе цепи не опережает воздействие.
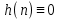
-Физически нереализуемая
Контр. пример
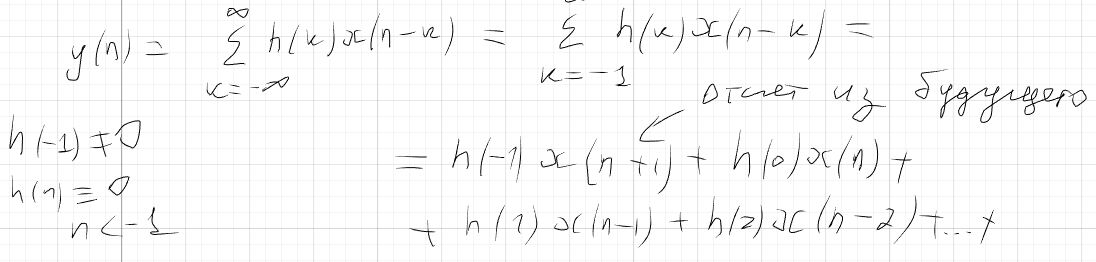
y(n) – отчет реакции в данный момент времени
2. (материал из методички) Основной характеристикой ЛДС в частотной области является частотная характеристика (ЧХ)
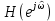 – Фурье-изображение ИХ h(n) :
– Фурье-изображение ИХ h(n) : 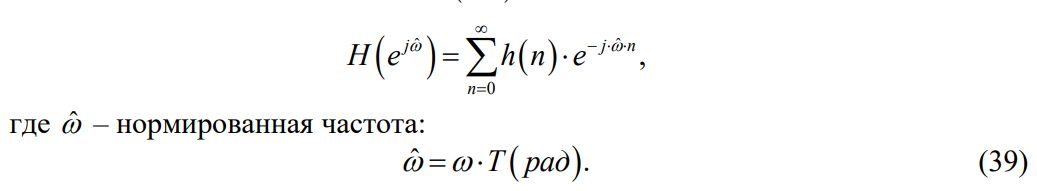
Частотная характеристика
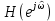 связана с передаточной функцией H z соотношением:
связана с передаточной функцией H z соотношением:
что позволяет путем подстановки
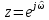 в (32) получить ее в виде:
в (32) получить ее в виде: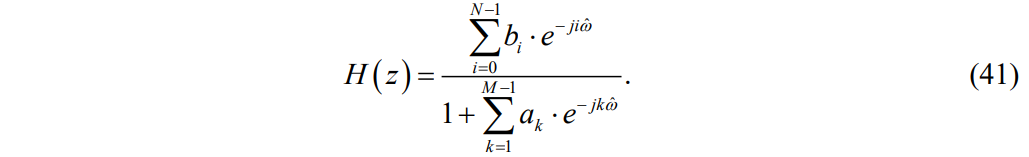
Про формулу 32.
Передаточной функцией ЛДС называют отношение z-изображения реакции к z-изображению воздействия при ННУ:
Данное отношение легко получить, выполнив Z-преобразование РУ (30). Передаточная функция рекурсивной ЛДС имеет вид дробно-рациональной функции:
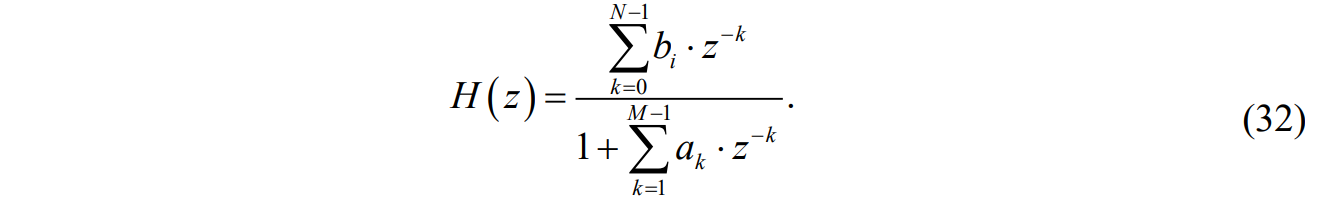
Показатель степени z-k соответствует задержкам воздействия b задержкам реакции; коэффициенты ak передаточной функции и РУ (30) имеют противоположные знаки.Соотношение вход/выход ЛДС, однозначно связанное с его основной характеристикой в z-области – передаточной функцией, имеет вид линейного математического преобразования в виде разностного уравнения (РУ):
Про формулу 30 из его электронной доски.
Разностное уравнение
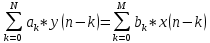
x(n) – воздействие
y(n) – реакция
k – значения задержек воздействия и реакции
ak, bk – вещественные коэффициенты (параметры) РУ
N, M – константы, определяющие максимальные задержки
R = max(N, M) – порядок ЛДС (порядок фильтра)
РУ задаёт алгоритм для нахождения y(n)
3. (материал из методички) Амплитудно-частотная характеристика (АЧХ) отображает частотную зависимость отношения амплитуды реакции к амплитуде гармонического воздействия в установившемся режиме.
Фазочастотная характеристика (ФЧХ) отображает частотную зависимость разности фаз реакции и гармонического воздействия в установившемся режиме.
АЧХ и ФЧХ – периодические функции с периодом 2π в шкале частот
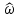 или fд в шкале частот f (Гц).
или fд в шкале частот f (Гц).АЧХ – четная, а ФЧХ – нечетная функция частоты.
АЧХ и ФЧХ рассчитываются в основной полосе частот [0; π] в шкале частот
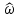 или [0; fд
или [0; fд
/2 ] в шкале частот f (Гц).