Файл: Автоматтандыру адамды технологиялы рдістерді басару міндеттерін тікелей орындаудан босатып, бл міндеттерді автоматты рылылара артумен сипаттайтын кешенді механикаландыру кезеі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 417
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, бастапқыдан алыстап кетеді.
Сондықтан реттеуішті таңдау дұрыстығын негізінен реттеуіштің параметрлерін анықтау үшін есептік, қажет болса эксперименттік мәндермен нақтылайды. Сонымен қатар, бұл мәндерді тек (орныққан) режим үшін ғана емес, динамикалық (өтпелі) үрдістер үшін де алады.
Жүйенің динамикалық қасиеттерін оқып игергенде оған кіретін барлық элементтерді динамикалық саласы бойынша қарастырады.
Автоматты жүйенің өтпелі үрдісі бүтін немесе бөлек буындарында сызықты немесе бейсызықты дифференциалды теңдеулермен жазылады. Жүйенің жалпы теңдеуін бөлек буындар теңдеуімен құрастырады.
Талдау және синтездеу кезінде қажет болатын бөлек элементтердің және нақты жүйенің жұмыс принципін, жүйе жұмысын ауызша түсіндіруге болады.
Бірақ ауызша сипаттама жүйенің жұмыс сапасының сандық бағасын бермейді. Сондықтан жүйенің жұмыс істеу принципі және мақсаты бойынша әр түрлі жүйелерді бағалау және салыстыру мүмкін болу үшін математикалык модель деп аталатын математикалык сипаттама қолданылады. Модельдер түпнұсқаның маңызды қасиеттерін көрсетеді. Қандай да бір нақты зерттеулерге аз әсер ететін маңызьі жоқ факторлар ескерілмейді. Сондықтан бір нысанды әр түрлі зерттеуде әр түрлі модельдермен ұсынуға болады.
Элементтік сипаттамада сигналдың физикалық қасиеттері негізінде элементтерді жүйеге біріктірілетін жүйеге бөлік кіретін құрылымдық және фуңкционалдық элементтер мен байланыстарға теңдеу алады. Теңдеудің сол бөлігіне элементтердің физикалық шығыс айнымалыларын немесе олардың уақыт бойынша туындысын қосады, оң бөлігі - элементке әсерін және физикалық кіріс айнымалылар. Бөлек айнымалылар бір элементке кіріс болса, бір элементке шығыс болады. Мұндай сипаттамада айнымалылар саны басқарылатын айнымалылар санынан көп болуы мүмкін, себебі аралық айнымалыларға ие. Мұндай сипаттамалар жүйенің әр элементінің әсерін бөлек зерттей отырып, сол бойынша жүйенің жұмысын бағалайды.
Барлық жүйенің математикалық сипаттамасы қажет емес аралық сипатгамаларды шығарып тастап теңдеудің сол бөлігіндегі басқарылатын шамалар және оның туындылары ғана оң бөліктегі жүйеге басқарылатын әсерлерді алады. Барлық жүйенің сипаттамасы әр элемент жұмысын бөлек-бөлек талдау арқылы емес, жұмысты толығымен сипаттауга мүмкіндік береді.
Қазіргі зерттеулерде жүйенің динамикалық күйін бағалауға екі әдіспен бірге жүйенің динамикалық қасиетін жазықтықта бейнелейтін декарт координатасын ғана қолданып қана қоймай, кеңінен жүйенің динамикадағы жағдайын жазықгықта жағдай айнымалылары және жағдай жазықтығы деген түсініктерді пайдалана отырып бейнелейді.
Дифференциалды теңдеулерді құрастыруды тұрақты ток генераторы теңдеуін құру мысалында қарастырамыз.
Генератор үшін басқарылатын шама ретінде якорь қысқыштарындағы кернеуді қабылдаймыз, басқару әсері қоздыру орамына келіп түсетін кернеу болады. Жүктеме - ауытқу ретінде якорь тоғын немесе жүктеме параметрлерін (кедергі, индуктивтілік) қабылдаймыз. Генератор жылдамдықтан тұрақты, орам температурасы өзгермейді, гистерезис болмайды, якорь рөакциясы компенсацияланатын, якорь индуктивтілігі және жүктеме аз (оларды ескермеуге болады) деп есептейміз. Айтылғандарды ескергенде генератор якорь тізбегінің теңдеуі келесідей жазылады: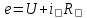
,
мұндагы e - генератордың ЭҚК;
U - басқарылатын кернеу:
R - якорь орамының кедергісі;
i - жүктеме тогы.
Ауытқуда
.
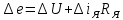Генератордың ЭҚК қоздыру тогының бейсызықты функциясы болып табылады (6.1-сурет), сондықтан жанама әдісі бойынша генератор бос жүріс сипапаманың сызықтылығын
6.1 -сурет. Генөратордың бос жүріс сипаттамасы
жасаймыз. Жұмыс нүктесі ретінде А қабылданады, мұнда і – і , сонда аламыз
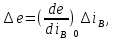
мұнда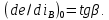
ӘҚК қоздыру ормының Ф магнит ағынына пропорционалды деп қабылдаймыз, сонда
е=cФ,
мұндағы с – генератордың құрылысына және айналу жылдамдығына тәуелді болатын тұрақты.
Ауытқуда
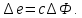
Қоздыру тізбегі
,
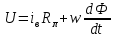мұндағы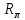
- қоздыру орамының кедергісі; Ф – оның магниттік ағыны; w-орам саны.
Ауытқуда
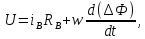
Яғни, тұрақты ток генераторы төрт теңдеулі жүйемен жаэылатындығын аламыз. Аралық айнымалылар
Ф, іш
,
е мүшелер топтамасын жойғаннан кейін генератордағы үрдісті сипаттайтын бір дифференциалдық тендеу аламыз
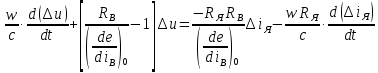(6.1)
6.1-теңдеу өте үлкен, ондағы айнымалылар кернеу және ток көлеміне ие. Мұндай теңдеуді қолданған ыңғайсыз. сондықтан уақыттан басқа теңдеуге кіретін барлық айнымалы шамалар жазбаның шексіз формасын қабылдайды. Мұндай формаға ауыстыру үшін теңдеудің әрбір қосылғышын осы қосылғышқа кіретін айнымалы шамасына тең тұрақты шамаға бөлу және көбейту қажет. Мұндай шама ретінде әдетте айнымалының номиналды орныққан мәнін санайды. (6.1) теңдеуі өлшемсіз формада келесідей жазылады.
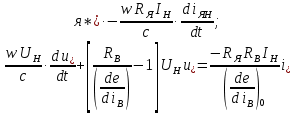
мұндағы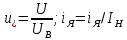
өлшемсіз шамалар.
(6.1) теңдеу коэффициент төмен туынды кезінде бірге тең болған жағдайда стандартты формаға келтіріледі. Стандартты форманы алу үшін (6.1) теңдеудің сол және оң бөлігін төменгі туынды кезіндегі
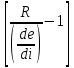U,коэффициентке бөлеміз.
T1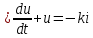
*
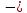T2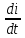
,(6.2)
Мұнда
T1=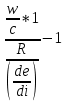
;
k=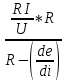
;
T2=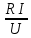
T1
(6.2)теңдеу генератордағы үрдістер сипатын анықтауға мүмкіндік береді және генератор кернеуіне барлық параметрлердің әсер етуін орнатады.
Стандартты жазу формасымен берілген операциялық қолданады. Әдеттегіден еш айырмашылығы жоқ, тек жинақы болып келеді.
A3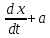
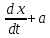2 1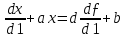
0 ƒ (6.3)
Операторлық түрде
(a3 p3+a2 p2+a1p+a0)x(1)=(b1p+b0)ƒ(t) (6.4)
Операторлық теңдеу (6.4) дифференциалдық теңдеу болып табылады , онда p әріпі дифференциалдау операторын білдіреді, ал x(t) және f(t) айнымалылары уақытының шынайы функциясы болып табылады.
6.2 Лаплас түрленуі
Автоматикалық жүйелердің есептеулерінде және зерттеулерінде аппас түрлерінуі де аталатын математикалық әдіСке жиі сүйенеді. Бұл әдіс бір айнымалының x(t) функциясын басқа айнымалының x(р) функциясына келесідей байланыс арқылы түрлендіруге мүмкіндік береді.
X(p)=ƒx(1)e-pt dt (6.5)
мұндағы р=a+jb – еркін комплексті шама
Әдеттегіден еш айырмашылығы жоқ, тек жинақы болып келеді.
Егер(6.2) түрдегі стандартты кіретін шамаларды u.. i тағы басқа белгілесек жіәне дифференциалдану операторының символын енгізсек
d/dt=p; d2/dt2=p2; d3/ dt3=p3 …
Онда элементтің немесе жүйенің дифференциалдық теңдеуі
A3
2 1
0 ƒ (6.3)
Операторлық түрде
(a3 p3+a2 p2+a1p+a0)x(1)=(b1p+b0)ƒ(t)(6.4)
Операторлық теңдеу (6.4) дифференциалдық теңдеу болып табылады , онда p әріпі дифференциалдау операторын білдіреді, ал x(t) және f(t) айнымалылары уақытының шынайы функциясы болып табылады.
x(t) функциясы түп нұсқа, ал x(р)-бейне деп аталады.
Лапас түрленуіне қысқартылған түрде келесідей
X(p)=Ʌ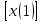
(6.6)
Лаплас түрленуіне дифференциалдық теңдеудің алгебралануын орындауға мүмкіндік береді, яғни дифференциалдау мен интегралдау операцияларын алгебралық көбейту және бөлу операцияларымен алмастыру. Бұл жағдайда x-тен бірінші туынды рx(р) бейнесіне ие болады, екінші- р2x(р), үшінші – р3x(р), n-ретті туындыны x(р) бейнесіне n-дәрежелі р операторының туындысы ретінде көрсетеді.
Ʌ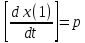
n x(p) (6.7)
X-тен интегралды алымында x(р),ал бөлімінде р бейнеленетін бөлшекпен алмастырады.
Ʌ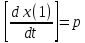 n x(p)(6.8)
Егер Лаплас түрленуіне дифференциалды теңдеуде қолданылса,онда Нөлдік бастапқы шартта ол келесідей жазылады:
( a0 pn+a1pn-1+…an-1p+a)y(p)=
=(b0pm+b1pmm-1+…am-1p+bm)x(p)(6.9)
Диффренциалды теңдеудің мұндай жазылу формасы операциялық деп аталады. Нөлдік бастапқы шарт деп басқару жүйесі тұратын буындардың шығыс шамалары бастапқы моментте нөлдік мәнге ие болуын айтады,егер олар бірінші ретті теңдеулермен жазылса, бірінші туындының қосымша нөлдік мәніне ие, егер олар 2- ретті теңдеумен жазылса және т.б
6.3 Статистикалық қасиеттер
Жүйенің статистикалық қасиеттерін сипаттамасы бойынша бағалайды. Жүйенің немесе буынның статистикалық сипаттамасы деп у басқарылаиын шаманың x кіріс шамадан тәуелділігін айтады, онда жүйе сызықтық болады және у=kx
Бейсызықты тәуелділікте жүйені бейсызықты деп есептейді.
Беріліс коффиценті жүйенің немесе буынның жұмысын орныққан режимде сипаттайтын негізгі параметрі болапы табылады. Беріліс коэффицентінің мәні статистикалық сипаттадан шығыс және кіріс өслерінің қатынасы арқылы табылады:
Жүйеге кіретін буындар тізбектей немсе параллельді жалғана алады.
Тізбектей жалғанылған жағдайда жүйенің жалпы беріліс коэффиценті k оның бөлек буындарының беріліс коэффиценттерінің k1,k2,k3… арына тең k= k1*k2*k3… .
Параллель жалғанған жағдайда жалпы беріліс коэффиценті әрбір буынның беріліс коэффиценттерінің қосындысына тең : k=k1+k2+k3+…kn
Бейсызықты жүйелер үшін беріліс коэффицентін беймызықты объектінің беріліс коффицентіндей анықтайды.
Статистикалық режимдегі жүйе жұмысының маңызды сапалы көрсеткіші болып табылады.
Статистикалық қателіктерді ажыратылған және тұйықталған автоматты жүйелер үшін деп бөледі. Егер, ажыратылған үйеде салыстырмалы статистикалық қателік тең болса, онда k3 беріліс коэффиценті бар тұйықталған статистикалық жүйеде статистикалық қателік 1+ k3 есе азаяды, яғни
Y=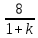
(6.10)
Жүйеге ергілікті кері байланыспен қамтылған буын кіргенде k3 бұл буынның беріліс коэффиценті келесідей есептеледі.
K3=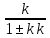
(6.11)
Мұндағы kp-буынның беріліс коэффиценті; kо.с-жергілікті кері байланыстың беріліс коэффиценті;
Теңдеуде (+) таңбасы теріс кері байланысқа жатады, ал(-) таңбасы оң. Буынды теріс ергідікті кері байланыспен қамтыған жағдайда беріліс коэффиценті азаятындығы (k3 < kр) және оң болған жағдайда – көбейтіндігін (k3 > k0) теңдеу көрсетеді. Автоматты жүйенің тиімділігі дәлдік дәрежесімен бағаланады-автоматтандырылмаған басқару обьектісінің (реттеуші жоқ) статистикалық қателігінің x0, автоматты жүйенің статистикалық қателігіне x қатынасымен (6.2-сурет) Неғұрлым дәлдік дәрежесі жоғары болса, соғұрлым жүйе тиімді жұмыс істейді.
Астатикалық жүйе үшін статистикалық қателіктің мәні және статистизм қателігі нөлге тең, ал дәлдік дәрежесі-шексіздікке.
Жүйенің немесе әрбір буынның статикалы сипаттамасын экспериментті түрде алуға немесе есептуге болады.
Сондықтан реттеуішті таңдау дұрыстығын негізінен реттеуіштің параметрлерін анықтау үшін есептік, қажет болса эксперименттік мәндермен нақтылайды. Сонымен қатар, бұл мәндерді тек (орныққан) режим үшін ғана емес, динамикалық (өтпелі) үрдістер үшін де алады.
Жүйенің динамикалық қасиеттерін оқып игергенде оған кіретін барлық элементтерді динамикалық саласы бойынша қарастырады.
Автоматты жүйенің өтпелі үрдісі бүтін немесе бөлек буындарында сызықты немесе бейсызықты дифференциалды теңдеулермен жазылады. Жүйенің жалпы теңдеуін бөлек буындар теңдеуімен құрастырады.
Талдау және синтездеу кезінде қажет болатын бөлек элементтердің және нақты жүйенің жұмыс принципін, жүйе жұмысын ауызша түсіндіруге болады.
Бірақ ауызша сипаттама жүйенің жұмыс сапасының сандық бағасын бермейді. Сондықтан жүйенің жұмыс істеу принципі және мақсаты бойынша әр түрлі жүйелерді бағалау және салыстыру мүмкін болу үшін математикалык модель деп аталатын математикалык сипаттама қолданылады. Модельдер түпнұсқаның маңызды қасиеттерін көрсетеді. Қандай да бір нақты зерттеулерге аз әсер ететін маңызьі жоқ факторлар ескерілмейді. Сондықтан бір нысанды әр түрлі зерттеуде әр түрлі модельдермен ұсынуға болады.
Элементтік сипаттамада сигналдың физикалық қасиеттері негізінде элементтерді жүйеге біріктірілетін жүйеге бөлік кіретін құрылымдық және фуңкционалдық элементтер мен байланыстарға теңдеу алады. Теңдеудің сол бөлігіне элементтердің физикалық шығыс айнымалыларын немесе олардың уақыт бойынша туындысын қосады, оң бөлігі - элементке әсерін және физикалық кіріс айнымалылар. Бөлек айнымалылар бір элементке кіріс болса, бір элементке шығыс болады. Мұндай сипаттамада айнымалылар саны басқарылатын айнымалылар санынан көп болуы мүмкін, себебі аралық айнымалыларға ие. Мұндай сипаттамалар жүйенің әр элементінің әсерін бөлек зерттей отырып, сол бойынша жүйенің жұмысын бағалайды.
Барлық жүйенің математикалық сипаттамасы қажет емес аралық сипатгамаларды шығарып тастап теңдеудің сол бөлігіндегі басқарылатын шамалар және оның туындылары ғана оң бөліктегі жүйеге басқарылатын әсерлерді алады. Барлық жүйенің сипаттамасы әр элемент жұмысын бөлек-бөлек талдау арқылы емес, жұмысты толығымен сипаттауга мүмкіндік береді.
Қазіргі зерттеулерде жүйенің динамикалық күйін бағалауға екі әдіспен бірге жүйенің динамикалық қасиетін жазықтықта бейнелейтін декарт координатасын ғана қолданып қана қоймай, кеңінен жүйенің динамикадағы жағдайын жазықгықта жағдай айнымалылары және жағдай жазықтығы деген түсініктерді пайдалана отырып бейнелейді.
Дифференциалды теңдеулерді құрастыруды тұрақты ток генераторы теңдеуін құру мысалында қарастырамыз.
Генератор үшін басқарылатын шама ретінде якорь қысқыштарындағы кернеуді қабылдаймыз, басқару әсері қоздыру орамына келіп түсетін кернеу болады. Жүктеме - ауытқу ретінде якорь тоғын немесе жүктеме параметрлерін (кедергі, индуктивтілік) қабылдаймыз. Генератор жылдамдықтан тұрақты, орам температурасы өзгермейді, гистерезис болмайды, якорь рөакциясы компенсацияланатын, якорь индуктивтілігі және жүктеме аз (оларды ескермеуге болады) деп есептейміз. Айтылғандарды ескергенде генератор якорь тізбегінің теңдеуі келесідей жазылады:
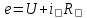,мұндагы e - генератордың ЭҚК;
U - басқарылатын кернеу:
R - якорь орамының кедергісі;
i - жүктеме тогы.
Ауытқуда
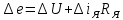.Генератордың ЭҚК қоздыру тогының бейсызықты функциясы болып табылады (6.1-сурет), сондықтан жанама әдісі бойынша генератор бос жүріс сипапаманың сызықтылығын
6.1 -сурет. Генөратордың бос жүріс сипаттамасы
жасаймыз. Жұмыс нүктесі ретінде А қабылданады, мұнда і – і , сонда аламыз
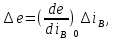
мұнда
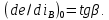
ӘҚК қоздыру ормының Ф магнит ағынына пропорционалды деп қабылдаймыз, сонда
е=cФ,
мұндағы с – генератордың құрылысына және айналу жылдамдығына тәуелді болатын тұрақты.
Ауытқуда
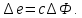
Қоздыру тізбегі
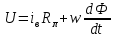,мұндағы
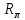- қоздыру орамының кедергісі; Ф – оның магниттік ағыны; w-орам саны.Ауытқуда
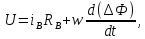
Яғни, тұрақты ток генераторы төрт теңдеулі жүйемен жаэылатындығын аламыз. Аралық айнымалылар
Ф, іш
,
е мүшелер топтамасын жойғаннан кейін генератордағы үрдісті сипаттайтын бір дифференциалдық тендеу аламыз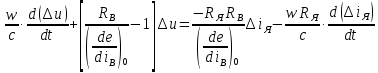 (6.1)6.1-теңдеу өте үлкен, ондағы айнымалылар кернеу және ток көлеміне ие. Мұндай теңдеуді қолданған ыңғайсыз. сондықтан уақыттан басқа теңдеуге кіретін барлық айнымалы шамалар жазбаның шексіз формасын қабылдайды. Мұндай формаға ауыстыру үшін теңдеудің әрбір қосылғышын осы қосылғышқа кіретін айнымалы шамасына тең тұрақты шамаға бөлу және көбейту қажет. Мұндай шама ретінде әдетте айнымалының номиналды орныққан мәнін санайды. (6.1) теңдеуі өлшемсіз формада келесідей жазылады.
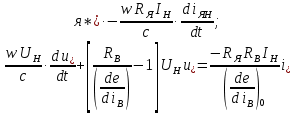
мұндағы
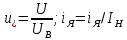өлшемсіз шамалар.(6.1) теңдеу коэффициент төмен туынды кезінде бірге тең болған жағдайда стандартты формаға келтіріледі. Стандартты форманы алу үшін (6.1) теңдеудің сол және оң бөлігін төменгі туынды кезіндегі
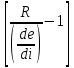U,коэффициентке бөлеміз.T1
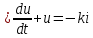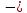* T2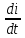 ,(6.2)Мұнда
T1=
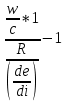;k=
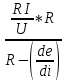;T2=
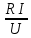T1(6.2)теңдеу генератордағы үрдістер сипатын анықтауға мүмкіндік береді және генератор кернеуіне барлық параметрлердің әсер етуін орнатады.
Стандартты жазу формасымен берілген операциялық қолданады. Әдеттегіден еш айырмашылығы жоқ, тек жинақы болып келеді.
A3
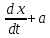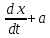2 1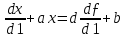 0 ƒ (6.3)Операторлық түрде
(a3 p3+a2 p2+a1p+a0)x(1)=(b1p+b0)ƒ(t) (6.4)
Операторлық теңдеу (6.4) дифференциалдық теңдеу болып табылады , онда p әріпі дифференциалдау операторын білдіреді, ал x(t) және f(t) айнымалылары уақытының шынайы функциясы болып табылады.
6.2 Лаплас түрленуі
Автоматикалық жүйелердің есептеулерінде және зерттеулерінде аппас түрлерінуі де аталатын математикалық әдіСке жиі сүйенеді. Бұл әдіс бір айнымалының x(t) функциясын басқа айнымалының x(р) функциясына келесідей байланыс арқылы түрлендіруге мүмкіндік береді.
X(p)=ƒx(1)e-pt dt (6.5)
мұндағы р=a+jb – еркін комплексті шама
Әдеттегіден еш айырмашылығы жоқ, тек жинақы болып келеді.
Егер(6.2) түрдегі стандартты кіретін шамаларды u.. i тағы басқа белгілесек жіәне дифференциалдану операторының символын енгізсек
d/dt=p; d2/dt2=p2; d3/ dt3=p3 …
Онда элементтің немесе жүйенің дифференциалдық теңдеуі
A3
2 1 0 ƒ (6.3)Операторлық түрде
(a3 p3+a2 p2+a1p+a0)x(1)=(b1p+b0)ƒ(t)(6.4)
Операторлық теңдеу (6.4) дифференциалдық теңдеу болып табылады , онда p әріпі дифференциалдау операторын білдіреді, ал x(t) және f(t) айнымалылары уақытының шынайы функциясы болып табылады.
x(t) функциясы түп нұсқа, ал x(р)-бейне деп аталады.
Лапас түрленуіне қысқартылған түрде келесідей
X(p)=Ʌ
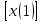
(6.6)
Лаплас түрленуіне дифференциалдық теңдеудің алгебралануын орындауға мүмкіндік береді, яғни дифференциалдау мен интегралдау операцияларын алгебралық көбейту және бөлу операцияларымен алмастыру. Бұл жағдайда x-тен бірінші туынды рx(р) бейнесіне ие болады, екінші- р2x(р), үшінші – р3x(р), n-ретті туындыны x(р) бейнесіне n-дәрежелі р операторының туындысы ретінде көрсетеді.
Ʌ
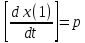n x(p) (6.7)X-тен интегралды алымында x(р),ал бөлімінде р бейнеленетін бөлшекпен алмастырады.
Ʌ
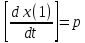n x(p)(6.8)Егер Лаплас түрленуіне дифференциалды теңдеуде қолданылса,онда Нөлдік бастапқы шартта ол келесідей жазылады:
( a0 pn+a1pn-1+…an-1p+a)y(p)=
=(b0pm+b1pmm-1+…am-1p+bm)x(p)(6.9)
Диффренциалды теңдеудің мұндай жазылу формасы операциялық деп аталады. Нөлдік бастапқы шарт деп басқару жүйесі тұратын буындардың шығыс шамалары бастапқы моментте нөлдік мәнге ие болуын айтады,егер олар бірінші ретті теңдеулермен жазылса, бірінші туындының қосымша нөлдік мәніне ие, егер олар 2- ретті теңдеумен жазылса және т.б
6.3 Статистикалық қасиеттер
Жүйенің статистикалық қасиеттерін сипаттамасы бойынша бағалайды. Жүйенің немесе буынның статистикалық сипаттамасы деп у басқарылаиын шаманың x кіріс шамадан тәуелділігін айтады, онда жүйе сызықтық болады және у=kx
Бейсызықты тәуелділікте жүйені бейсызықты деп есептейді.
Беріліс коффиценті жүйенің немесе буынның жұмысын орныққан режимде сипаттайтын негізгі параметрі болапы табылады. Беріліс коэффицентінің мәні статистикалық сипаттадан шығыс және кіріс өслерінің қатынасы арқылы табылады:
Жүйеге кіретін буындар тізбектей немсе параллельді жалғана алады.
Тізбектей жалғанылған жағдайда жүйенің жалпы беріліс коэффиценті k оның бөлек буындарының беріліс коэффиценттерінің k1,k2,k3… арына тең k= k1*k2*k3… .
Параллель жалғанған жағдайда жалпы беріліс коэффиценті әрбір буынның беріліс коэффиценттерінің қосындысына тең : k=k1+k2+k3+…kn
Бейсызықты жүйелер үшін беріліс коэффицентін беймызықты объектінің беріліс коффицентіндей анықтайды.
Статистикалық режимдегі жүйе жұмысының маңызды сапалы көрсеткіші болып табылады.
Статистикалық қателіктерді ажыратылған және тұйықталған автоматты жүйелер үшін деп бөледі. Егер, ажыратылған үйеде салыстырмалы статистикалық қателік тең болса, онда k3 беріліс коэффиценті бар тұйықталған статистикалық жүйеде статистикалық қателік 1+ k3 есе азаяды, яғни
Y=
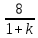(6.10)Жүйеге ергілікті кері байланыспен қамтылған буын кіргенде k3 бұл буынның беріліс коэффиценті келесідей есептеледі.
K3=
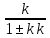(6.11)Мұндағы kp-буынның беріліс коэффиценті; kо.с-жергілікті кері байланыстың беріліс коэффиценті;
Теңдеуде (+) таңбасы теріс кері байланысқа жатады, ал(-) таңбасы оң. Буынды теріс ергідікті кері байланыспен қамтыған жағдайда беріліс коэффиценті азаятындығы (k3 < kр) және оң болған жағдайда – көбейтіндігін (k3 > k0) теңдеу көрсетеді. Автоматты жүйенің тиімділігі дәлдік дәрежесімен бағаланады-автоматтандырылмаған басқару обьектісінің (реттеуші жоқ) статистикалық қателігінің x0, автоматты жүйенің статистикалық қателігіне x қатынасымен (6.2-сурет) Неғұрлым дәлдік дәрежесі жоғары болса, соғұрлым жүйе тиімді жұмыс істейді.
Астатикалық жүйе үшін статистикалық қателіктің мәні және статистизм қателігі нөлге тең, ал дәлдік дәрежесі-шексіздікке.
Жүйенің немесе әрбір буынның статикалы сипаттамасын экспериментті түрде алуға немесе есептуге болады.