Файл: Автоматтандыру адамды технологиялы рдістерді басару міндеттерін тікелей орындаудан босатып, бл міндеттерді автоматты рылылара артумен сипаттайтын кешенді механикаландыру кезеі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 415
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6.2 сурет.
1 және 2- автоматтандырылмаған басқару обьектінің және автоматты жүйенің статистикалық сипаттамалары.
Статикалық сипаттаманы эксперименттік анықтауда жүйенің немесе буынның кіріс шамасына кезекпен әр түрлі мен беріп тұрады және өтпелі процестің жойылуына қажет уақыт өткен сайын шығыс шаманың мәнін жазып алып отырады. Алынғын нүктелер ретін сызықтап байланыстырып, үйенің немесе буынның статикалық сипаттамасын тұрғызады(6.3 сурет) Егер У шығыс шамасы тек кіріс x
Шамасына ғана емес, сонымен қатар h кейбір шамаларынан да тәуелді болса, онда статикалық сипаттамалар қатарын алады. Статикалық сипаттамалар бойынша әрбір x әсер беретін шамадан тәуелділігін көрсететін теңдеуге әкеледі, яғни сипаттаманың математикалық теңдеуін анықтайды. Есептеудің аналитикалық әдісі жүйенің кез келген параметрінің процеске әсерін көрсететін статикалық сипаттамалар теңдеулерін анықтауға мүмкіндік береді; алынған теңдеулерге параметрлерінің нақты бір мәнін немесе берілген мәндердің қойылуына жүгінбей берілген басқару процесінің жалпы заңдылықтарын анықтауға тамаларды есептеудің аналитикалық әдісі тек сызықтық және сызықталған жүйелерде ғана қолданылады.
Графоаналитикалық тәсілде сызықтық және бейсызықты жүйелерді талдау үшін жеке элементтердің статикалық сипаттамасын жеке элементке жазылған аналитикалық теңдеулер негізінде тұрғызылатын графиктер түрінде көрсетеді. Кейін аралық тәуелді айнымалыларды графикалық түрде жояды. Кеоі байланыспен қамтылған элементтер сипаттамаларын да графикалық тұрғызулармен табады.
6.4.Динамикалық қасиеттер.
Автоматты жүйелердің динамикалық қасиеттерін бағалау әр түрлі әдістермен орындалады. Бұл мақсатта дифференциалды теңдеулерді, беріліс функцияларын, кақыттық және жиіліктік сипаттамалрды қолданады.
Жүйені сипаттайтын дифференциалды теңдеулерді шешу кіріс әсерге (ауытқу) жүйенің реакциясымен түсіндіріледі. Кіріс әсерлер сипатына және шамасына қарай әр түрлі болатындықтан, теңдеудің шешімі де әр түрлі болады.
Мұндай кіріс әсер дара сатылы функция болып табылады.(6,4а-сурет). Дара сатылы функция немесетиптік әсер лездік қосылумен немесе ішкі сигналдың өшірілуімен түсіндіріледі. Ол 1 символымен белгіленеді және қгосылғанда келесідей жазылады.
6.4-сурет
Дара сатылы функциямен қатар кіріс сигнал импульс түрінде берілсе дара импульсті функция қолданылады. Өтпелі процесс теңдеулері, яғни жүйенің типтік әсерге реакциясын графикалық түрде бейнелеуін уақыттық немес екпіндеу сипаттамасы деп атайды. Ол нөлдік шарттарда дара кіріс әсері бірдей ішкі әсер үшін жүйе қозғалысы немее элементі дифференциалдық еңдеуінің шешімін көрсетеді.
Жүйенің динамикалық қасиеттерін операциялық теңдеулерден алынатын беріліс функциясы арқылы да бағалайды.
Жүйенің немесе элементтің беріліс функциясы шығыс шаманың Лаплас бейнесінің сәйкес нөлдік бастапқы шартта кіріс шаманың Лаплас бейнесіне қатынасымен түсіндіріледі,яғни әлеуметтік немесе жүйе тыныш күйде болуы қает шартта.
Жалпы түрде жүйенің беріліс функциясы операциялық теңдецмен келесідей
теңдеуінің бөлігі болып табылады. Беріліс функциясымен қатар жүйе динамикасын амплитуда және фазаның жүйе немесе буын арқылы өтетінсинусоида тербелістерінің жиілігінен тәуелділігін көрсететін жиіліктік сипаттамалармен бағалайды. Жиіліктік сипаттамалрды алу үшін жүйе немесе буын кірісіне типтік әсер ретінде периодты түрде өзгеріп отыратын кіріс сигналын беріп отырады. Шығысында кіріс сигналына тәуелді басқа фазалы және амплитудалы бірақ бастапқы жиіліктегі сигнал пайда болды. Жүйе немесе буын кірісіне тұрақты амплитудалы және әр түрлі жиілікті гармоникалық әсерлер бере отырып, шығысында бұрышына ығысқан, және басқа амплитудалы синусоидалы тербелістер пайда болады. Алынған әр түрлі жиіліктер үшін х және у мәндерә бойынша жиіліктік сипаттамалрды алады: амплитудалы, фазалы және амплитудалы-фазалы.
Амплитудалы жиілікті сипаттама шығыстағы гармоникалық әчер тербелісі амплитудасының оның кірістегі теобеліс жиілігінен тербеліс амплитудасына қатынасы.
Фазалы жиілікті сипаттамасы(ФЖС) тербеліс жиілігінен кіріс және шығыс тербелістер арасындағы фазалар айырмашылығынң тәуелділігін көрсетеді.
Кіріс гармоникалық әсерге түрлі жиіліктерді бере отырып, нәтижесцнде жиілікті сипаттамалрды тұрғызатын нүктелер сериясын алады.
Амплитудалы-фазалы жиіліктік сипаттаманы (АФЖС) амплитудалы және фазалы сипаттамалар негізіндн тұрғызады. ОСы мақсатпен (ФЖС) графигінде нақты жиілік үшін фаза мәнін анықтайды, оны көлденең осьтен бұрыш түрінде алады. Тура осылай (АФЖС) қисығын алатын басқа жиіліктер үшін нүктелер анықталады. Жиіліктік сипаттамаларды экспериментті анықтаудың жолы осылай.
Егер ажыратылған жүйенің немесе буынның беріліс функциясының теңдеуіне қойсақ, онда комплексті жазықтықтағы жорамал және заттық бөліктерінің геометриялық қосындысы түрінде келтірілген немесе жиіліктік функциясының теңдеуін аламыз.
6.5. Типтік динамикалық буындар.
Автоматты жүйелерде оқып игеренде элементтердің функционалды белгілері боцынша жіктелуімен бірге олардың динамикалық қасиеттері бойынгша іктелуі кеңінен қолданылады. Динамикалық буын немесе буын деп автоматикалық жүйенің нақты динамикалық қасиеттеріне ие бөлігін түсіне отырып, автоматты жүйелер тұратын физикалық қондырғылардың әртүрлілігін салыстырмалы түрде көрсетуге мүмкіндік береді.
Типтік буындар күшейткіш, инерциясыз,апериодты,дифференциалдаушы,интегралдаушы,тербеліс және кешігу буындары болып бөлінеді.
Күшейткіш инерциясыз буында шығыс шама у кез келген уақыт моментінде кіріс шамаға х тікелей пропорционалды Мұндай буын теңдеуі
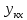(6.19)Мұнда к-буынның беріліс коэффиценті.
Бұл буынның динамика теңдеуі оның статикалық теңдеуімен сәйкес келеді.
Оның кірісіне дара әсер берілуімен алынатын буынның уақыттың сипаттамасы суретінде көрсетілген.
6.5- сурет.
Буынның беріліс коэффиценті (6.5, а-сурет)
W(p)
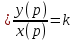(6.20)Жиіліктік функция немесе инерциясыз буынынң АФЖС W (jῳ ) = k. (6.5,е – сурет ) заттық ось бойынша Р (ῳ) координата басынан к арақашықтығында орналасқан нүктемен түсіндіріледі. (6.19) теідеуінен х = Anx sinwt кіріс теңдеуінде шығыс сигнал тең болады
y = Aкір sinῳt (6.21)
Инерциясыз буында шығыс және кіріс сигналдар фазада болады (6.5, г-сурет)
Φ(ɷ) = 0, (6.22)
ал, шығыс сигналының амплитудасы (6.5, д – сурет) кіріс сигналының амплитудасынан k есеге өзгеше.
K(ɷ)= k (6.23)
Инерциясыз буынның жиілікті сипаттамалары жиіліктен тәуелсіз екендігін (6.22) және (6.23) көрсетіп тұр. Инерциясыз буынға мысал ретінде электронды тұрақты ток күшейткіштерін, редукторларды, үйкеліссіз түрлі типті тетіктер, датчиктерді жатқызуға болады.
Апериодты буын бірінші және екінші ретті бола алады, сонымен қатар екінші жағдайда оны бірінші ретті екі апериодты буынның тізбектей қосылуы ретінде көрсетуге болады. Бірінші ретті апериодты буындарда кірісіне дара функция түрінде сигнал бергенде шығыс шама жаңа орныққан мәнге жетіп апериодты өзгереді. Мұндай буынды жиі инерциялық, бір сыйымдылықты немесе статикалық деп атайды.
Бірінші ретті апериодты буын келесідей дқифференциалды теңдеумен жазылады.
T
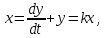(6.24)мұнда k – беріліс коэффициенті; T – уақыт тұрақтысы.
Беріліс функциясы
W(p)
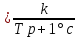(6.25)Апериодты буынның АФЖС
W(jῳ )
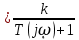(6.26)Амплиутудалы және фазалық сипаттамарды (6.25) теңдеуін шешу арқылы алуға болады. Бірақ теңдеуді шешу арқылы емес, АФЖС қолдану арқылы табу оңай.
(6,26) тедеуінде нақты және жалған бөліктерін ерекшелейміз, сол үшін теңдеу бөлімін кездесетін санға көбейтіп, түрленуден кейін нақты
P (ɷ )
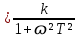(6.27)Q (ɷ )
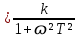(6.28)жиіліктік сипаттамаларды табамыз.
(6.27) және (6.28) теңдеулерін қолдану арқылы амплитудалық және фазалық сипаттамалрды табамыз.
амплитудалы
K (ɷ)=
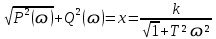(6.29)және фазалы
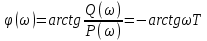(6.30)Периодты буын сүзгі қасиетіне иес, яғни кіші жиілікті сигналды жақсы және үлкен жиілікті сигналдарды нашар өткізеді сондықтан К (
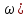жиіліктің өсуімен азаяды (6.6, в – сурет), сонымен қатар шығыс сигналының амплитудасы да азаяды.Фазалық жиілікті сипаттама (6.29) шығыс сигналдар кіріс сигналдан фаза бойынша қалып отыратындығын көрсетеді. Қалу шамасы 0
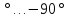аралығында болады. Жиілік 
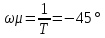сыну жиілігі деп аталады. Уақыт тұрақтысы Т буынның инерциялық өлшемін сипаттайды.Өтпелі процесс t = (4…5)T уақытында аяқталады. Т мәні неғұрлым көп болған сайын, соғұрлым апериодтық буын өз қасиеті бойынша инерциясыздыққа жақын болады. 6.6 – суретте бірінші ретті апериодты буынның сипаттамалары және шартты белгіленулері көрсетілген. Мұндай буынға электр машиналарының қоздыру орамдарын, магнитті күшейткіштердің басқару орамдарын жатқызуға болады.
Екінші ретті периодты буын дифферециалды теңдеулер арқылы жазылады.
T
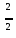
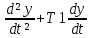+y=kx. (6.31)T1
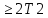болғанда буындағы қуат шығыны өте көп және онда тербелістер пайда болмайды. Мұндай буын (6.28) теңдеуімен жазылатын екі тізбектей қосылған бірнеше апериодты буындар түрінде көрсетіледі.Буынның беріліс функциясы
W (p) =
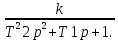(6.32)Амплитудалы – фазалы жиіліктік сипаттама
W(jῳ) =
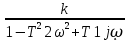. (6.33)Амплитудалы сипаттама
K(
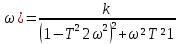
(6.34)
6.6 – сурет. Бірінші ретті апериодты буын:
а – шартты белгіленуі; б- уаққытты сипаттама; в- амплитудалы сипаттама; г- фазалы сипаттама; д- амплитудалы- фазалы сипаттама; е- буын мысалы
Фазалы сипаттама
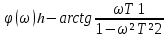(6.35)Шартты белгіленулер, уақыттық және амплитудалы- фазалы, жиілікті сипаттамалары 6.7 – суретте көрсетілге.
Екінші ретті апериодты буынға жылытқыш қондырғылар, жылыжай, кептіргіш агрегаттар және т.б жатады.
Дифференциалды буында кіріс шамадан уақыт бойынша туындыға пропорционалды шығыс шама, басқаша айтқанда, шығыс шама кіріс шаманың өзгеру жылдамдығына пропорционалды. Идеалды және реалды дифференциалдаушы буындар болып бөлінеді.
Идеалды дифференциалдаушы буын теңдеуі
y=k
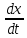(6.36)Жиіліктік сипаттамалар: амплитудалы – фазалы және фазалы:
W(jῳ) = kjῳ; K (
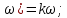(6.37)Реалды дифференциалдаушы бун теңдеуі
T
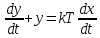(6.38)Беріліс функциясы
W (p)=
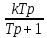(6.39)6.7 – сурет.
Жиіліктік сипаттамалар: амплитудалы- фазалы, амплитудалы және фазалы
W(jῳ) =
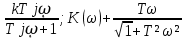; (6.40)
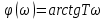.Идеалды буынның шартты белгілнулері, уақыттық және жиіліктік сипаттамалары 6.8 – суретте көрсетілген. Мұндай буынды шығыс кедергісі нөлге тең сұлба түрінде көрсетуге болады. Буын шығысындағы кіріс шамалы секірмелі түрде өзгергенде, теориялық шексіз үлкен амплитудаға ие болатын лездік шығыс импульсі пайда болады.
Реалды буынның уақыттық және АФЖС 6.8, ж, 3- суреттерде көрсетілген. Мұндай буынды R және С элементтері бар төрт полюстік түрінде көрсетуге болады (6.8, и- сурет). (6.36) теңдеуін қанағаттандыратын идеалды буынды жасап шығару мүмкін емес. (6.40) теңдеуінде көрсетілгендей неғұрлым Т аз және Л көп болса, сғұрлым реалды дифференциалдаушы буын идеалдыға жақын болады.
Неғұрлым Е көп болса, соғұрлым дифференциалдаушы буын кұшейткіштікке жақын, ал Т =
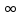болғанда күшейткітікке айналады. Уақыт тұрақтысының Е мәнін жанама әдісі арқылы анықтауға болады Т=RC.