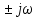Файл: Автоматтандыру адамды технологиялы рдістерді басару міндеттерін тікелей орындаудан босатып, бл міндеттерді автоматты рылылара артумен сипаттайтын кешенді механикаландыру кезеі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 412
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Интегралдаушы буында шығыс шама кіріске берілетін шамның уақыт бойынша интегралына пропорционалды. Ол келесі теңдеумен жазылады
y (t)= k
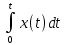 (6.41)
(6.41)Егер теңдеудің оң және сол біліктерін дифференциалдасақ, онда (6.41)
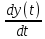 =kx(t) (6.42)
=kx(t) (6.42)(6.40) теңдеуі интегралдаушы буынның шығыс шамасының өзгеру жылдамдығы кіріс шамаға пропорционалды екендігін көрсетеді. Беріліс коэффициенті к бірлік шаманың дара
6.8- сурет.
Мәнінде шығыс шаманың өзгеру жылдамдығына тең. Егер кіріс және шығыс шамалар бірдей бірлікке өлшенсе, беріліс коэффициентінің өлшем бірлігі с1. Мұндай жағдайларды беріліс коэффицентін емес интегралдаушы буынның Т= 1/k уақыт тұрақтысын қолданады. Онда (6.42) теңдеу келесідей түрде болады.
T
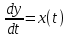 (6.43)
(6.43)Беріліс функциясы
W(p)=
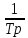 (6.44)
(6.44)Жиіліктік сипаттамалар: амплитудалы-фазалы, амплитудалы және фазалы .
W(jῳ)=
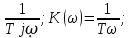 (6.45)
(6.45)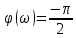
Интегралдаушы буынның шарты белгіленулері, уақыттық және жиіліктік сипаттамалары 6.8 – суретте көрсетілген. 6.8, б- суретте және (6.41) теңдеуінен көрініп тұрғандай, буын кірісіне тұрақты әсер бергенде оның шығысында
6.9- сурет.
уақыт өтуімен сызықты өсетін шама пайда болады. Бұл буын есте сақтау болмысының қасиетіне ие, яғни кіріс әсердің жоқ болып кеткен уақыттағы болған шығыс шаманың мәнін сақтап қалады. Мұндай буынға мысал ретінде электромагнитті және электромеханикалық уақыт тұрақтысын ескермегенде тұрақты ток қозғалтқыштарын сыйымдылықты интегралдаушы кондурды (6.9, е-сурет) келтіруге болады. Буынның амплитудалық сипаттамасы жиіліктің өсуімен азаяды сондықтан шығыс шаманың амплитудасы да азаяды. Буын жиіліктен тәуелсіз 90° тең теріс Фаза ығысуын енгізеді.
Тербеліс буыны деп кірісіне дара әсер бергенде шығыс шама гармоникалық иербелістер жасай отырып орныққан мәнге жететін буынды есептейді.
Тербеліс буынының дифференциалдық теңдеуі
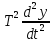 + 2T
+ 2T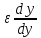 + y = kx (6.46)
+ y = kx (6.46)Мұндағы
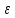 – өшу коэффиценті T – уақыт тұрақтысы.
– өшу коэффиценті T – уақыт тұрақтысы.Тербеліс буынына мысал ретінде электр тізбектерін (6.10 с-сурет) келтіруге болады. Кірісінде
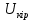 кернеуі болғанда сыйымдылық С электр өрісінің энергиясының (потенциалды энергия) жинайды, ал индуктивтілік L – электромагниттік өріс энергиясын (кинетикалық энергия) жинайды. Сондықтан тербеліс буынын әр түрлі энегрия түрін жинау қасиетіне ие тізбектей қосылған екі элемент түрінде қарастыруға болады. Энергиялар алмасқанда өзара алмасу болып жатқан арнада қайтарылымсыз шығындар пайда болады (электр тізбегі үшін R кедергісінде). Бұл шығындардың өлшемі өшу коэффиценті
кернеуі болғанда сыйымдылық С электр өрісінің энергиясының (потенциалды энергия) жинайды, ал индуктивтілік L – электромагниттік өріс энергиясын (кинетикалық энергия) жинайды. Сондықтан тербеліс буынын әр түрлі энегрия түрін жинау қасиетіне ие тізбектей қосылған екі элемент түрінде қарастыруға болады. Энергиялар алмасқанда өзара алмасу болып жатқан арнада қайтарылымсыз шығындар пайда болады (электр тізбегі үшін R кедергісінде). Бұл шығындардың өлшемі өшу коэффиценті
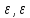 көп болса, энергия шығыны дакөп болады. Егер 1 >
көп болса, энергия шығыны дакөп болады. Егер 1 > >0, онда өтпелі процесс тербелмелі сөнбелі және
>0, онда өтпелі процесс тербелмелі сөнбелі және  көп болса, соғұрлым тербеліс тез басылады. Мұндай буынды орнықты деп атайды. Тербеліс буынының уақыт тұрақтысы оның резонансты жиілігі
көп болса, соғұрлым тербеліс тез басылады. Мұндай буынды орнықты деп атайды. Тербеліс буынының уақыт тұрақтысы оның резонансты жиілігі 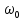 арқылы анықталады T = 1/
арқылы анықталады T = 1/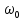 және ол резонансты тербелістер периодынан 2
және ол резонансты тербелістер периодынан 2 есе аз
есе аз 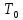 =2Л/
=2Л/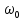 = 2
= 2 Т
ТБуынның беріліс функциясы
W(p)=
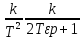 (6.47)
(6.47)Жиіліктік сипаттама
Тербелмелі буынның жиіліктік сипаттамалары
 коэффицентінен тәуелді. Егер тербеліс кезінде буындағы энергия қоры азаймай көбейетін болса, онда тербеліс амплитудасы өсетін болады, мұндай буын орнықсыз деп аталады.
коэффицентінен тәуелді. Егер тербеліс кезінде буындағы энергия қоры азаймай көбейетін болса, онда тербеліс амплитудасы өсетін болады, мұндай буын орнықсыз деп аталады.Тұрақсыз тербелмелі буынның динамика теңдеуі
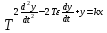 (6.48)
(6.48)6.10-суретте орнықсыз тербелмелі буынның шартты белгіленуі, уақыттық және амплитудалы-фазалы жиіліктік сипаттамалары бейнеленген.
Егер
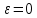 онда мұндай буын гармоникалық тербелмелі (консервативті) буын деп аталады.
онда мұндай буын гармоникалық тербелмелі (консервативті) буын деп аталады.6.10-сурет.
6.11-сурет.
6.12-сурет.
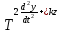 (6.50)
(6.50)Консервативті буынның беріліс, жиіліктік, амплитуалды және фазалы сипаттамалары келесідей түрге ие
Бұл сипаттамалардың графикалық бейнеленуі 6.12-суретте көрсетілген.
Кешігу буыны кіріс әсерді бұрмалаусыз береді, бірақ сонымен қатар оны кейбір тұрақты шамаға кешіктіреді, яғни шығыс шама кіріс шамаға қатысты t тұрақты шамаға кешігеді. Мұндай қасиеттерге құбырлар, шығынсыз электр желілері, транспортерлер және т.б. ие.
Кешігу буыны келесі теңдеумен жазылады
y(t)=(t-

)x (6.51)
Буынның беріліс функциясы, жиіліктік, амплитудалы, фазалы сипаттамалары келесідей жазылады
W(p) =
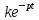 ; W(j
; W(j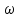 )=
)=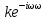 ; (6.52)
; (6.52)K(
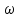 ) = k;
) = k; 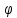 =-
=-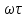
Бұл буындардың амплитудалы сипаттамалары бірдей және фазалы сипаттамалары әр түрлі. Бұл буын амалсыз тербелістердің жиілігінен тәуелді теріс фаза ығысуын жасайды.
6.6 Сызықты жүйелердің орнықтылығын талдау
Жұмыс істеп тұрған автоматты жүйеге әр түрлі тұрақты сыртқы қоздырулар әсер етуі себебінен реттелетін шығыстық шаманың мәні жиі өзгеріп отырады. Жүйенің автоматты реттеуші осы реттелетін шаманы тапсырылған мәнге келтіруге ұмтылады. Бірақ тұтастай алғанда жүйеде инерциялық массалар, реактивті элементтер (индуктивтік, сыйымдылық) болатындықтан оның орнықты қалпына келуі немесе қалыптасқан бір күйден келесісіне өтуі лезде емес, белгілі түрде кешігіп жүзеге асады. Жүйеде өтпелі процесс туындйды. Бұл жағдайда егер жүйе қоздыру әрекеті тоқталғаннан кейін қалыптасқан күйге оралса, ол орнықты. Егер оралмаса, онда орнықсыз. Орнықсыз жұмыс кері байланыспен қамтылған АРЖ-ның барлығында туындауы ықтимал.
Қазіргі автоматты жүйелерде мынадай үш талаптар орындалуы қажет: орнықтылық шарты, өтпелі процеске және қалыптасқан режимге қойылатын талаптар. АРЖ-ның орнықтылығын анықтау мәселесі басты болып саналады, өйткені орнықсыз жүйелер іс жүзінде жарамсыз. Орнықтылықты зерттеудің жалпы әдісі АРЖ-ның g(t) жоспарлау (басқарушы) және f(t) қоздыру әсерлері тудыратын y(t) реттелетін шаманың өзгеруі үшін жазылған
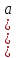 )y(t) =
)y(t) ==
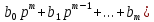 g(t)
g(t)дифференциал теңдеуін талдаумен тұжырымдалады. g(t). f(t) мәндерін және олардың туындыларын нөлге тең деп алсақ сипаттама теңдеуі
G(p)=
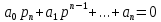 (6.53)
(6.53)болатын біртектес
(
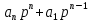
+…+
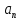 ) y(t)=0 (6.54)
) y(t)=0 (6.54)Диффренциал теңдеуін аламыз.
АРЖ-ның орнықты екендігін (6.59) теңдеуін шешу арқылы анықтауға болады. Оның шешімі өтпелі процесті сипаттайды
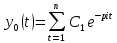 (6.55)
(6.55)мұндағы
 – интегралдау тұрақтысы, ол бастапқы шарттан анықталады;
– интегралдау тұрақтысы, ол бастапқы шарттан анықталады; 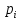 – сипаттамалық теңдеудің түбірлері.
– сипаттамалық теңдеудің түбірлері. 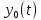 өтпелі процесс саны
өтпелі процесс саны 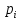 түбірлер санымен анықталатын құраушылар қосындысынан тұрады.
түбірлер санымен анықталатын құраушылар қосындысынан тұрады.Жүйе орнықты түрде болуы үшін (6.60)-нің шешімі мына шартты қанағаттандыруы тиіс:
lim
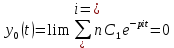 (6.61)
(6.61)Бұл өрнек орнықтылық шартының аналитикалық өрнегі болады. Жалпы жағдайда
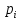 түбірлері комплекстік болып келеді. Оған қоса олар түйіндес
түбірлері комплекстік болып келеді. Оған қоса олар түйіндес 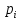 ,
, 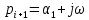 түбірлердің жұбын түзейді. Егер түбірлер айғақты болса (p=
түбірлердің жұбын түзейді. Егер түбірлер айғақты болса (p=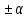 ) онда
) онда 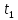 уақыт мезетінде ықпал берілгеннен кейінгі өтпелі процестің сипаты экспоненциалды түрде болады. Түбір шамасы p= +
уақыт мезетінде ықпал берілгеннен кейінгі өтпелі процестің сипаты экспоненциалды түрде болады. Түбір шамасы p= + болғанда өтпелі процесс тарап кетеді де, жүйе орнықсыз болады, алp=-
болғанда өтпелі процесс тарап кетеді де, жүйе орнықсыз болады, алp=- кезінде процесс өшіп, жүйе орнықты болады. p=
кезінде процесс өшіп, жүйе орнықты болады. p=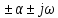 комплекс түбір болғанда өтпелі процесс тербелмелі болады, яғни
комплекс түбір болғанда өтпелі процесс тербелмелі болады, яғни 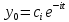 sin (
sin (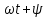 ). Егер түбірдің айғақты (нақты) бөлігі теріс болса (p=-
). Егер түбірдің айғақты (нақты) бөлігі теріс болса (p=-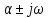 ) онда тербеліс өтпелі яғни жүйе орнықты болады. p=
) онда тербеліс өтпелі яғни жүйе орнықты болады. p=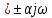 түбірдің айғақты бөлігі оң болғанда процесс тарап кетеді де жүйе орнықсыз болады.
түбірдің айғақты бөлігі оң болғанда процесс тарап кетеді де жүйе орнықсыз болады.Егер түбір p=