Файл: Автоматтандыру адамды технологиялы рдістерді басару міндеттерін тікелей орындаудан босатып, бл міндеттерді автоматты рылылара артумен сипаттайтын кешенді механикаландыру кезеі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 407
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
7.2. Өтпелі үрдіс қисығын тұрғызу әдістері
Өтпелі үрдіс көрсеткіштерінің сандық мәнін анықтайтын уақыттық немесе өтпелі функцияның графигін модельдеу және есептеу жолдары арқылы экспериментті түрде алуға болады.
Өтпелі үрдістің қисығын экспериментті түрде анықтағанда автоматты жүйе болуы қажет, яғни басқару обьектісі және реттеуіш. Басқарылатын шама y(t) өзгерісін кірісте жалғыз қоздыру болғанда 1(t) уақыт бойынша тіркей отырып, өтпелі үрдіс қисығын алады. Мұндай әдісті жүйенің сол немесе басқа бөлігінің болмауынан немесе сынақ жасау мүмкін болмағандықтан кез келген жағдайда іске асыру мүмкін емес.
Модельдеу әдісі. Бұл мақсаттар үшін барлық шешілетін тапсырмаларды қамтитын интегралды бағдарламалық жүйелер және бағдарламалар пакеттері қолданылады. Соның ішінде математикалық есептерді автоматтандыруға арналған Reduce, Derive, TK Solver, Mathcad, Mathematica, MapleV, MATLAB және т.б. MATLAB математикалық есептерді автоматтандыру жүйесі осы аймақтағы ең көнесі болып табылады. MATLAB жүйесі математикалық, инженерлік, ғылыми және техникалық есептемелер үшін жоғары дәрежелі бағдарлама тілі ретінде MathWorks, Inc фирмасымен жасалып ұсынылған болатын. Жүйе даму үрдісінде әр түрлі қосымша пакеттермен ұлғайып отырды, яғни жүйе мүмкіндіктері жоғарылай түсті. Бірақ сонымен қатар оны бірінші кезеңде меңгеру қиындығы ұлғайды.
Басқа да компьютерлік бағдарламалар сияқты MATLAB жүйесінің артықшылықтарымен қатар кемшіліктері де бар. Жүйенің артықшылықтары анық және жоғарыда аталып, өткен, тек бұл жүйеде бағдарламалар жазылуының жеңілдігін атап өту қажет. Жүйенің кемшіліктеріне формулалар мен өрнектердің сызықты жазылуын жатқызуға, мысалы Mathcad жүйесімен салыстырғанда оқуға ыңғайсыздау және алғашқы кезеңде оқып игеруге қиындық туғызатын жүйенің үлкенділігін жатқызуға болады.
Қазіргі кезде MATLAB жүйесіне арналған әдебиеттер үлкен көлемде.бірақ осы әдебиеттер бағдарламаның барлық мүмкіндіктерін қамти алмайды.
Есептік әдіске дифференциалдық теңдеулерді шешуге және жиіліктік әдіске негізделген әдістерді жатқызады. Дифференциалдық теңдеулерді аз қолданылатын және кейбір қиындықтарды туғызатын классикалық және операциялық әдсіпен шешуге болады. Дифференциалдық теңдеуді операциялық әдіспен шешу белгілі сурет бойынша функцияның түпнұсқасын табуға әкеледі, яғни Лапластың кері түрлендіруі жолымен.
У(t) өтпелі функциясын оның F (p) бейнесі бойынша келесі теңдеуден табады.
Y (t) =
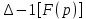(7.2)F (p)бейнесін W3(p) тұйық контурдың беріліс функциясы теңдеуінен табуға болады.
Y (p) =W3 (p) x(p). (7.3)
Егер x(t) =I(f) қабылдасақ , онда шығыста Y(t) ие боламыз. Жалғыз сатылы функция бейнесі 1/p тең,онда
F (p) =
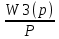(7.4)Онда
Y (t) =
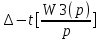(7.5)Бейне кестелерін қолдана отырып, түпнұсқа мәнін табады.
Амплитудалы-фазалы және жиіліктік сипаттамалар қасиеттеріне негізделген жиіліктік әдісті өтпелі үрдіс қисықтарын тұрғызуда басқаларға қарағанда жиі қолданады. Оның басты артықшылығы, затты сипаттаманы қолдана отырып салыстырмалы қарапайым әдіс бойынша басқару өтпелі үрдісінің жақындатылған қисығын тұрғызуға болады және сол бойынша үрдіс көрсеткіштері анықталады.
7.3. Сапаны жанама бағалау.
Өтпелі үрдіс шешімі күрделі және үлкен тапсырмалардан тұратын бір қатар параметрлер мен сипатталады. Практикалық тапсырмаларды шешекенде сапаның барлық көрсеткіштері қажет етілмейді. Сондықтан басқару сапасын зерттеу үшін өтпелі үрдіс қисығын тұрғызбау үшін өтпелі үрдісті бағалаудың жанама әдісі қолданылады. Өтпелі үрдістің бөлек қасиеттерін оны тұрғызбай сипаттайтын шамаларды жанама баға деп атайды. Өтпелі үрдіс сапасының бірнеше жанама бағасы бар: жиелікті сипаттама бойынша баға, интегралды баға, түбірлі әдіс және т.б. Көп тарағаны жиеліктік сипаттама бойынша баға. 7.2- суретте тұйықталған автоматты жүйенің амплитудалы К(
) және фазалы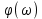 
жиіліктік сипаттамалары көрсетілген. Амплитудалық сипаттамада бірнеше сипаттық аймақтарды ерекшелеуге болады: ab аймағында шығыс сигналының амплитудасы кіріс сигналының амлитудасына тең, яғни К (ω)=1; bc аймағында резонансты жиелік нүктесінде амплитуда максималды мәңге ие А max , жиілік одан әрі жоғарылаған сайын жүйе өзінің интелсиялылығының әсерінен үлкен жиелік тербелістеріне әсер етіп үлгере алмайды және К(ω) лезде төмендейді –de аймағына. Шығыс сигнал кіріс сигналдан фаза бойынша қалып отырады, сондықтан фазалық сипаттама кері. 
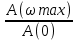= M қатынасын тербеліс коэффиценті деп атайды. М жоғары болған сайын өтпелі үрдіс тербелмелі болып келеді. Жалпы М =1,2...1,5. Аз М - ға реттеудің үлкен уақыты сәйкес келеді, жүйе қобалсыз әсер теуге әсер етеді. М үлкен болғанда қайта реттеу ұлғаяды және жүйе орнықтылық шегіне жақындай бастайды.
АЖС үшін ω max жиілігімен қатар ω с3 және ωа жиілікті сипатта болып келеді. ω с3 жиілігін тұйықталған жүйенің қию жиілігі деп атайды және оның мәнін шығыс және кіріс тербелістері амплитудалары өзара тең болғанда К(ω)= 1 деңгейінде анықтайды.
ω n жиілігі тұйықталған жүйенің өткізу жолы деп аталады және А (0)/= 0,707 ретінде анықталады. Ол жүйенің дәлдігімен тез әрекеттілігіне әсер етеді, оның өсуімен жүйенің тез әрекеттілігі де өседі, ω n көп болған сайын кіріс сигналының көптеген спектрі бұрмалаусыз беріледі, яғни соғұрлым жүйе жұмысының дәлдігі жоғарылайды.
Тұйықталған жүйенің М тербелмелігі және ω n өткізу жолы өтпелі үрдіс сапасының жанама көрсеткіштері болып табылады және сол бойынша жүйе жұмысын сипаттауға болады.
Басқару сапасының бағасын логарифмді жиілікті сипаттама бойынша орындауға болады. Ол үшін ашық жүйенің ЛАЖС енгізілген. Басқару үрдісінің көрсеткіштері мен типтік ЛАЖС параметрлері арасындағы санды байланыс алдын ала анықталған және номограмма түрінде болады. Солар бойынша жанама және тікелей көрсеткіштерді анықтайды. Интегралды және тамырлық әдістер арқылы жүйенің сапа көрсеткіштерін анықтау туралы арнайы әдебиеттерден оқып танысуға болады.
7.2-сурет. Автоматты жүйенің жиіліктік сипаттамалары а-амплитудалы және фазалы , б-логарифмды.
7.4. Орныққан қателіктерді анықтау.
Басқарудың автоматты жүйесі жұмыс үрдісінде оның кірісіне түскен сигналдары беруі және жүргізуі қажет. Ол сигналдардың жүргізу дәлдігі жүйе қателіктерімен бағаланады. Қателіктерді ажыратады: берілген әсер бойынша,
E(t)= x(t)-y(t), (7.6)
яғни, кіріс әсер x(t) және басқарылатын шама y(t) арасындағы айырмашылығын көрсететін әсер бойынша және басқарылатын шама өзгерісіне сәйкес келетін қобалжу әсер бойынша
E(t)-y(t), (7.7)
Орныққан қателік шамасы t=
уақыт мәні үшін есептелеі , яғни E(t)орн=lime(t) (7.8)
Орныққан қателіктер мәнін анықтаудың бірнеше әдістері бар, қарапайым түрде ол қателіктің беріліс функциясы көмегімен анықталады.
E(p)=W o (p)x(p) (7.9)
Уақыт функциясы ретінде қателікті анықтау үшін кері Лаплас түрленуін жасайды және t
ұмтылғанда E(t)=
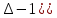(7.10)Берілген әсерден орныққан қателік мәнін Лапластың кері түрленуін қолданбай анықтауға болады.
E(t)= limр W o(p)x(p) (7.11)
Қателіктің беріліс коэффициенті
Wо(p)=
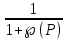(7.12)Сонда
E (F) = lim
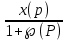(7.13)статикалық жүйе үшін W(0)=K, ал жеке типті әсердің x(t)= x0
E(t)=
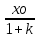(7.14)Мұнда к-тұйықталмаған жүйенің беріліс коэффициенті.
Қобалжу әсерінен орныққан қателікті келесі теңдеу бойынша анықтайды.
E ((t) орн=limWf(p))F(p) (7.15)
Мұнда Wf (p)- қобалжу бойынша беріліс коэффициенті
Wf(p)=
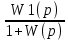(7.16) Онда қобалжу әсерінен орныққан қателік
E(t)орн=limp
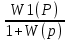F(p) (7.17)Статикалық обьект және статиткалық реттеуіш үшін W1 (0) =k0 және W (0) =k0 К p Секірмелі қобалжу болғанда F (t)=Fo онда F (p) = Fо/ p және орныққан қателік
E(t)орн=
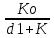Fo (7.18)Мұнда К = КоКp-ашық жүйенің беріліс коэффициенті
(7.18) теңдеуінің Fо түрлі мәніне орныққан қателіктің түрлі мәндері сәйкес келетіндігін көруге болады.
8.1. Жалпы мағлұматтар
Бейсызықты жүйелілерді зерттеу үшін жоғарыда қарастырылаған бейсызықты сипаттамаларды сызықтау әдістеріне негізделген гармониялық баланс, статистикалық сызықтау және фазалық траекториялар әдістері қолданады.
Құрамына бейсызықты статикалық сипаттамасының бір элементі кіретін автоматты басқару жүйесін бейсызқты автоматты жүйесі деп аталады. Жеке элементтердің статикалық сипаттамаларының бейсызықтылығын әр түрлі себептермен түсіндіруге болады.
Құрастырылып отырған жүйелерді зерттеу кезінде және элементтің де және толық жүйенің де статикалық сипаттамаларының линеризациялауға ұмтылады. Бірақ біраз бейсызықты элементтері бар жүйелердің әсерінен олардың қозғалысын сызықты немесе линерезация теңдеуі арқылы жазуға келмейтін жүйелерде кездемеді. Сондықтан динамикалық сипаттамалары бейсызықты дифференциялық теңдеумен жазылатын алдында қаралған тәсілдерді бейсызықты жүйелерді талдауға қолдануға келмейді, себебі мұндай теңдеулерді шешетін тәсілдер жоқ.
Бейсызықты автоматты жүйе басқару параметрінің аз ауытқуында орнықты болуы мүмкін және үлкен ауытқуда орнықсыз болуы немесе барлық кезде орнықсыз болуы мүмкін.
Бейсызықты жүйелердің математикалық моделін сызықты жүйелерді құрайды. Автоматты басқару жүйесінің негіздік, міндеттік және алгоритмді құрылымдық сұлбаларын құрастырады. Әр флемент үшін бсқарылатын парметрлер сипаттамаларын табады. Егер бейсызықты өтпелі үрдістің сипатына аз әсер етсе, оны линеризациялайды , бейсызықты таза білінсе сақтайды. Осыған байланысты кейбір бейсызықты беріліс функциясы бар және зфенолардың бейсызықты сипаттамасы бар алгоритмдік құрылымдық сұлбаны алады.
Автоматты бейсызықты жүйенің жеке құрамын талдау үшін жақын тәсілдер реті ұсынылған, соның ішінде фазалық жазықтық, гармоникалық баланс және математикалық модельдеу тәсілодері кеңінен тарлған. Бейсызықты жұйелерді зерттеуде ең маңызды тапсырма –автотербеліс режимі құрылатын және оның параметрін бағалау жағдайын анықтау болып табылады. Бейсызықты жүйелердің автотербелісі сыртқы әсердің нәтижесінен пайда боламайды, оның айрықша динамикалық құрамынан пайда болады. Бейсызықты жүйелерді талдаудың жеке тәсілдерін қарастырамыз.
8.2.Фазалық траектория.
Автоматтандыру жүйесінің күйі сандармен сипатталуы мүмкін. Олар кеңістіктегі кейбір нүктелердің координаттары дер қарауға рұқсат етілген, соның ішінде осы кеңістіктің кез келген нүсктесіне жүйенің бір нақты күйі сәйкес келеді. Уақыттың өтуіне байланысты параметрлер өзгереді, сонымен қатар кеңістікте нүкте координаттары да өзгереді. Осыған байланысты, нүктелердің қозғалысы бойынша автоматты басқару жүйесінің тәртібін түсінуге болады. Жүйенің тәртібін сипаттайтын нүктені бейнелейтін нүкте деп, ал оның траекториясын - фазалық траектория деп, ал кеңістігін фазалық кеңістік деп атайды. Екінші ретті бейсызықты автоматты жүйені зерттеу үшін фазалық кеңістік фазалық жазықтыққа қосылады.
Демек, фазалық траектория және фазалық кеңістік жүйеде болатын динамикалық үрдіс туралы геометриялық көзқарасты көрсетеді.
Абцисса осі бойынша фазалық жазықтықта берілген мәннен басқарылатын шаманың у ауытқуын ординат осінде –оның өзгеру жылдамдығын орнатады. Екінші ретте теңдеумен жазылатын жүйе күйі кез-келген уақытта және мәндерімен анықталады. Өтпелі режимде және мәндері өзгереді және бейнелейтін нүкте фазалық жазықтықта әр түрлі жағдайда орны алады.
Берілген міннен басқарылатын шаманың ауытқуы сөнбейтін синусоидеалды гармоникалық тербелістерді көрсетеді делік. Оны фазалық жазықтықта және координаттарында бейнелейік. Уақыт моментінде синусоидалды тербелістер мәніне ие және А нүстесімен сипатталады деп есептелік. Өтпелі ұрдістің АВ учаскесінде параметрінің ауытқуы ұлғаяды, ал оның жылдамдығы
іздеген теңдеуді табамыз.
+
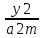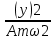= 1Бұл А және ωА жартылай осьті эллипс теңдеуі екеніне көз жеткізу қиын емес. Фазалық жазықтықта А әр түрлі мәндері кезінде қиылыспайтын және орталық деп аталатын ортақ нүсктеге ие эллипстің құрамдастарын аламыз. Период өткеннен соң автоматты жүйедегі өтпелі үрдіс F нүктесінде және А нүктесінде фазалық жазықтықта қатарласады . Соның салдарынан фазалық траекторияға арналған теңдеуді алуға болады, егер басқару шамасының ауытқуының өзгеру жылдамдығын тапса