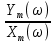
W(jω) = 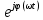= A(ω) 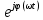(6.76)

А (ω) мен φ (ω) мәндері жиілікке тәуелді. А (jω) жиіліктік беріліс функциясын ω өзгергенде комплекс айнымалылар жазықтығында осы вектордың годографы, яғни амплитудалы-фазалы сипаттама (АФС) түрінде кескіндеуге болады.

Зерттелетін ашық жүйенің беріліс функциясын біле отырып және ондағы р операторды jω-ға алмастырып, жиіліктік сипаттаманы (АФС) алады. Тәжірибе жүзінде немесе есептеумен алынған АФС-ның түрі бойынша жүйе орнықты ма, жоқ па, соны анықтайды.

Орнықтылықтың Найквист критерийі былайша тұжырымдалады: егер тұйықталмаған күйдегі АРЖ орнықты болса, онда ол тұйықталған күйде де орнықты болуы үшін тұйықталмаған жүйенің амплитудалық-фазалық сипаттамасы координаты (-1,j0) нүктесін қамтымауы (айналып өтпеуі) қажетті әрі жеткілікті.

Орнықтылықтың қарастырылған тұжырымы тұйықталмаған жүйе орнықты болып, АФС теңдеуіндегі бөлшектің алымындағы полином дәрежесінен кем болғанда ғана дұрыс болады.

Тұйықталмаған жүйе орнықты және бейтарап буындардан құралғанда ғана орнықты болады. Бұл жүйенің құрылымдық схемасынан құрылған буындар құрамын қарастырғанда тағайындалады.
6.19-сурет.
АФС координаты (-1,j0) нүктені қамти ма, жоқ па соны анықтау үшін осы нүктеден АФС-ның арлық нүктелеріне вектор тұрғызылады. Егер жүйе орнықты болса,онда векторының қорытындысы нөлге тең. Ал орнықсыз жүйе үшін ол нөлге тең болмайды. Бұл бұрыш π/2 -ге тең. 2-қисық астатикалық жүйенің АФС-на сәйкес келеді. Астатикалық жүйенің беріліс функциясының көбейткіші 1/р, ал АФС-ын теңдеінікі 1/jω болады. Мұндай жүйенің АФС-ын салғанда ω → 0 болса, онда ол шексіздікке кетеді. 2-қисық (-1,j0) координаты бар нүктені қамти ма, жоқ па, сосын анықтау үшін оның -қисықтық айналық кескінін салады. Содан кейін 2 және қисықтарымен қиылысқанға дейін үлкен радиусты, центрі координат басында болатын m доғаны тұрғызады.

Егер [1 + W(jω)] векторының соңы o-q-a-b-m-n-a-r-o тұйықталған қисықпен өтсе, әрі (-1,j0) нүктесінің төңірегінде оның бұылысының қорытынды бұрышы нөлге тең болса, онда жүйе орнықты болады.

АФЖ-ның нақты осьтің теріс бағытымен қиылысу нүктесінде фаза бойынша ығысу 180º-қа тең, олай басқа шығыстық сиганл кіріспен қарсы фазада болады. Егер қиылысу нүктесі координаты (-1,j0) нүктенің сол жағында болса, онда шығыстық сигналы амплитудасының кіріске қатынасы бірден үлкен екенін білдіреді. Кері байланыс тізбегі тұйықталғанда жүйенің кірісіне амплитудасы мен фазасы ұлғайған сигнал келеді. Жүйе арқылы өте отырып, ол тағы да ұлғаяды. Демек, жүйе орнықсыз.

---

Мысал, Найквист критерийімен статикалық АРЖ-ны орнықтылыққа тексеру қажет.

Тұйықталмаған АРЖ-ның беріліс функциясы

W(p) =
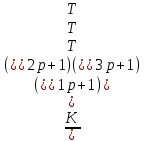
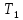= 90 с; 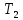= 10 с; 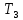= 3 с; 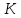= 20 кезінде 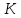= 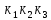р-ны ω-ға алмастырып, жиіліктік беріліс функциясын алады.
W(jω) =
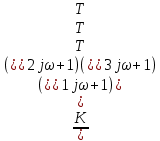
Формуладағы бөлшектің алымы мен бөлімін, соңғысына түйіндес комплекс санға көбейтіп, оны айғақты және жорамал бөлікке ажыратып алады.
6.20-сурет.

Формулаға буындардың уақыт тұрақтыларының мәндері мен тұйықталмаған мәндері мен тұйықталмаған жүйенің К күшейту коэффициентінің мәнін қойып, айғақты және жорамал бөліктерінің мәнін алады.

W(jw)=20[(1-1200₍₁₎²)-103 jm(1-26,2w²)] ;

[(1+8100w²) (1+100w²) (1+9w²)]

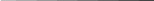U (w)= 20 ( 1-1200₍₁₎²) ;

[( 1+8100w²) ( 1+100w² ) (1+9w²)]

V (w)= - 20:103 jm (1-26,2₍₁₎²)] .

[(1+8100₍₁₎²) ( 1+100w²) ( 1+9 w²)]

U () мен V (w)- ның әр түрлі w үшін табылған мәндері 6.2- кестеге енгізілген. Кестедегі деректер бойынша АФС салынады. Жүйе орнықты, өйткені (-1,j0) нүкте қисықтың сол жағында қалады.

6.2- кесте

w. c-1	0	0,005	0,016	0,08	0,195	0,5	8
U (w)	20	16,2	4,4	-1,46	-0,5	-0,35	0
V (w)	0	-8,6	-10,4	-1,5	0	0,3	0

---

6.8. Орнықтылық қоры туралы түсінік
Автоматты басқару жүйесі екі себепке байланысты орнықсыз болуы мүмкін; динамикалық звенолардың сәйкес емес құрамы және звено параметрлерінің сәйкес емес мәні. Бірінші себеп бойынша АБЖ құрылымды орнықсыз деп аталады. Бұл АБЖ параметрлерін өзгерту арқылы оның орнықтылығына қол жеткізу мүмкін еместігін аңғартады, оның құрылымын өзгерту керек. Мысалы, егер АБЖ кез келген мәндегі инерациялық және тербелмелі звенолардан тұрады, амплитудалы- фазалы жиіліктік сипаттамалы тұйықталмаған контуры бар болса, 6.22- суретте көрсетілгендей.

АБЖ күшейту коэффициенті күшейген кезде оның АФЖС әр нүктесі ( К ) координат басынан алыстайды, АФЖС кейбір К _крит мәні кезінде (-1,j0) нүктесін кесіп өтпейінше. К ары қарай ұлғаюы кезінде АБЖ орнықсыз болады. Және керісінше, К кішіреюі кезіндегі АБЖ орнықты етуге болады,сондықтан оны құрылымды орнықты деп атайды. Егер АБЖ астатикалық болса, онда оның ажырауы кезінде сипаттамалық теңдеуі нөлдік түбірге ие, сондықтан w→ 0 кезінде, АБЖ к∞ ұмтылады. Мысалы,Wp ( p)= P(Tp+1)K болса, астатизм реті v=1, АБЖ тұйықталмаған АФЖС болады.
6.22-сурет.
6.23-сурет.
Алымы бөлімінен көп болғандықтан, w→0 кезінде P (w)→-∞,Q (w)→ - j∞ болады. Мұндай АФЖС 6.22- суретте келтірлген. АФЖС үзік болғанына байланысты оның (-1,j0) нүктесін қиып өтетіні туралы айту қиын. Мұндай жағдайда келесі тәсілді қолданады; егер АФЖС үзік болса,w→0 кезінде шексіздікке ұмтылса, онда оны ойша шексіз радиустағы жартылай шеңбермен толтырады, ол оң жартылай осьтен басталып, АФЖС теріс бағытымен жалғасады. Содан соң Найквист критерийін қолдануға болады. Суретте көрсетілгендей бір интегралды звеносы бар АБЖ құрылымды орнықты болып табылады.

Егер АБЖ екі интегралды звеносы бар болса (астатизм реті v=2), онда АФЖС екінші шаршыда шексіздікке ұмтылады.(6.24- сурет).

6.24 – сурет.

w→0 кезінде P(w)→∞,Q (w)→+j∞ тең болады. Мұндай АБЖ параметрлерінің кез келген мәндерінде орнықты болмайды, яғни ол құрылымды орнықсыз.

Құрылымды орнықсыз АБЖ орнықты етуге болады, ол үшін оған түзетуші звено қосу керек ( мысалы, дифференциялаушы немесе тездетуші) немесе АБЖ құрылымын өзгерту арқылы, мысалы, жергілікті кері байланыс арқылы.

---

Эксплуатациялау жағдайында жүйе параметрлері небір себептерге байланысты белгілі бір шектерде өзгеруі мүмкін ( ескіру, температуралық тербеліс және т.б). Мұндай тербелістер жүйенің орнықтылығын жоғалтуға әкеліп соғуы мүмкін, егер ол орнықтылық шегіне жақын жерде жұмыс істеп тұрса. Сондықтан АБЖ орнықтылық шегінен қашық жерде жұмыс істейді деп жобалауға тырысады. Мұндай алыстату дәрежесін орнықтылық қоры деп атайды. Найквист критерийіне сәйкес шекті нүктеден АФЖС неғұрлым қашық болса (-1, j0), соғұрлым орнықтылық қоры көп болады. Орнықтылық қорын модуль бойынша және фаза бойынша деп екіге бөледі. Модуль бойынша орнықтылық қоры тұйықталмаған АБЖ АФЖС годографының ось бағытындағы шекті нүктеден жоғалуын сипаттайды және шекті нүктеден абцисса осінде годографтен түйісу нүктесіне дейінгі арақашықтықпен h анықталады.( 6.25- сурет).

6.25- сурет.

Фаза бойынша орнықтылық қоры годографтың шекті нүктеден бір радиустағы шеңбер доғасы бойынша жоғалуын сипаттайды және координат басынан шеңберлі годограф түйіскен кері бағытты жартылай осьтің және сәуленің арасындағы бұрышпен анықталады. Тұйықталмаған АБЖ беріліс коэффициенті өскен сайын АФЖС әр нүктенің модулі өседі және K = K _кр кейбір мәндерінде АФЖС шекті нүктеден өтеді де орнықтылық шекарасына түседі,ал K > K_kp кезінде тұйықталған АБЖ орнықсыз болады.

Әдетте АБЖ құруда қажетті орнықтылық қорлары h және ⱷ беріледі, ол деңгейден аспауы керек. Бұл деңгейлер сектор түріндеқойылады және тұйықталмағаниАБЖ АФЖС кірмейтін шекті нүктенің сыртында сызылады.


W(jm)= К = K = Kw² T- jKw = P(w) +jQ(w)

jm (jwT-1) jw-w² T w₂w⁴ T²

7.1. Сапа көрсеткіштер
Автоматты басқару жүйесі тек орнықты болып қана қоймай, сонымен қатар басқару үрдісінің сапасын қамтамасыз ету қажет.Басқару жүйелерінің жұмысын бағалауға мүмкіндік беретін басқару сапасына қойылатын талабы басқару үрдісінің көрсеткіштері деп аталады. Олар өтпелі үрдістегі жүйенің жағдайын сипаттайды. 7.1, а- суретте жүйенің кіріске берілген жеке қобалжуы кезіндегі өтпелі үрдістің қисығы көрсетілген.

---

Бұл жерде сапа көрсеткіштері реттеу уақыты, қайта реттеу, үрдістің тербелмелілігі, орныққан қателік, өтпелі үрдістің өшу сипаты, орнықтылық қоры болып табылады. Әр көрсеткішті бөлек қарастырамыз.

Реттеу уақыты t_p жүйенің тез әрекет етуін сипаттайды және басқарылатын шаманың реттеуіштің сезгіш емес аймағына кіруінің өту уақыты периодына сәйкес келеді

.

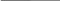a= y_max-y₀ 100%

y₀

Қайта реттеу деп - басқарылатын шаманың бастапқы мәннен у0 максималды ауытқуы ymax,пайызды түрде келесі өрнекте келтірілген.Қайта реттеу жүйе жаңа орныққан күйге А нүктесіне жанама иілу бұрышының тангенсімен анықталатын белгілі бір жылдамдықпен келетіндіктен пайда болады. Жылдамдық көп болған сайын қайта реттеу соғұрлым көп болады және оны азайту үшін басқарылатын шама жылдамдығының өсуін төмендету қажет. Бірақ жылдамдықты төмендету қажет. Бірақ жылдамдықты төмендету уақытының өсуіне алып келеді. Сондықтан қайта реттеу 20...30% аралығында болғанда оңтайлы деп есептелінеді.

Үрдіс тербелмелілігі басқарылатын шаманың реттеу уақытындағы тербеліс санымен сипатталады. Тербелмелілік санды түрде өшудің логарифмді декрементімен бағаланады. Өшудің логарифмді декременті неғұрлым жоғары болған сайын, өтпелі үрдістің өшуі соғұрлым тез болады.

Орныққан қателік орныққан режимдегі басқару дәлдігін көрсетеді. Ол басқарылатын шаманың бастапқы мәнімен номиналды жүктеме кезіндегі орныққан мәні арасындағы айырмашылық.

Өтпелі үрдістің өшу сипаты басқару жүйесіндегі өтпелі үрдістерді жіктеуге мүмкіндік береді және солардың ішінен негізгі төрт түрін ерекшелейді тербелмелі үрдіс оған қайта реттеудің бірнеше мәндері жатады- аз тербелмелі үрдіс бір қайта реттеуі бар үрдіс монотонды үрдіс бұл жағдайда басқарылатын шаманың өзгеру жылдамдығы өз таңбасын реттеу уақытында өзгертпейді апериодты үрдіс басқарылатын шама орныққан шамадан t , барлық мәніндегі сезгіш емес аймаққа дейінгі дәлдікпен аз болған жағдайдағы үрдіс.

---

Смотрите также файлы

• Контрольная работа по дисциплине Основы научных исследований и проектирования (вариант 6) Проверил.docx

• Правила внутреннего трудового распорядка работников муниципального казенного общеобразовательного учреждения Ихрекская средняя общеобразовательная школа.pdf

• Программа технической направленности робототехника.docx

• Лекция 22. Элементы физики лазеров 22 Спонтанные и вынужденные переходы.doc

• Мой дед уходил на войну, За Родину шел воевать.docx