Файл: Автоматтандыру адамды технологиялы рдістерді басару міндеттерін тікелей орындаудан босатып, бл міндеттерді автоматты рылылара артумен сипаттайтын кешенді механикаландыру кезеі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 413
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
жорамал болса тербеліс өшпейтін тұрақты амплитудалы болып келеді. Бұл орнықтылық шекарасы тербермелі деп аталады.
Орыс ғалымы, академик А.М.Ляпунов бірінші болып орнықтылықтың дәл анықтамасын тұжырымдап қозғалыстың орнықтылығын зерттеудің жалпы әдісін жасады. Оның теориясы бойынша сызықты АРЖ-ның орнықтылығы сипаттамалық теңдеудің түбірлерімен анықталады. Сызықтық АРЖ-ның орнықтылық шартының аналитикалық тұжырымын А.М.Ляпунов былайша тұжырымдайды: сызықты АРЖ орнықты болуы үшін мынадай шарттар қажетті және жеткілікті: сипаттамалық теңдеудің барлық айғақты түбірлерінің теріс таңбалы болуы, ал комплекс түбірлерінің айғақты бөлігі теріс таңбалы болуы тиіс.
Осылайша түбірлердің комплекс жазықтығында жорамал осі орнықтылық шекарасы болып табылады. Орнықтылық шекарасындағы бейтарап жүйе үшін жорамал осьте орналасқан түбірлердің болуы ал орнықсыз жүйе үшін жорамал осьтің оң жағында екм дегенде бір түбірдің болуы қажет.
Бірінші және екінші ретті жүйелердің сипаттамалық теңдеулерінің барлық коэффиценттері нөлден үлкен болса олар орнықты келеді. Жоғары ретті жүйе үшін бұл шарт тек қажетті ғана, бірақ жеткіліксіз. АРЖ-ның орнықтылығын әдетте орнықтылық критерийлерімен бағалайды. Орнылықтылықтың негізгі Раус - Гурвиц, Михайлов және Найквист критерийлері секілді үш критерийі бар. Олар жеке-жеке қарастырайық.
6.7. Орнықтылықтың алгебралық критерийлері
Раус - Гурвиц критерийі. Кейде алгебралық деп аталатын Раус - Гурвиц критерийінің мәні былайша анықталады:
G (p) =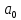
+ 
+ … + 
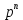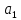
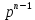= 0. (6.62)
Сипаттамалық теңдеудің түбірлері жорамал осьтің сол жағында жатып және жүйе орнықты болуы үшін Гурвицтің барлық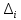
диагональ минорлары сипаттамалық теңдеудің оң коэффициенттері кезінде оң болуы қажетті әрі жеткілікті. Сипаттамалық теңдеуден Гурвицтің бас анықтауышы мынаған тең:
Осы анықтауышты құрағанда диагональ бойымен коэффициенттерді өспелі дәреже бойынша жазады. (6.63)-дегі үзік сызықпен таңбаланған барлық диагональ минорлары
> 0 кезінде оң болуы тиіс. Мысалы, бірінші ретті жүйе үшін
+ 
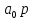= 0 (6.64)
орнықтылық шарты
> 0; > 0.
Екінші ретті жүйе үшін
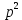+ р + 
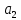= 0
Қажетті және жеткілікті шарт орындалу үшін сипаттамалық теңдеудің барлық коэффициенттері оң болуы тиіс: > 0; 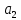> 0; >0.
Үшінші ретті жүйе жүйе үшін
+ 
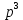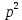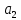+ р +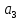
= 0 (6.66)
(6.66) сипаттамалық теңдеуінің барлық коэффициенттері, оған қоса екінші ретті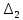
және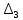 
анықтауыштары оң болуы қажетті әр жеткілікті.
Осылайша, үшінші және төртінші ретті теңдеулер үшін коэффициенттердің оң болуынан басқа (6.66) теңсіздіктерінің орындалуы да қажет.
Михайлов критерийі. Бұл критерийді А.В. Михайлов 1936 жылы жариялаған. Ол сызықты тұйықталған автоматты реттеу жүйелерін зерттеуге арналған. Автоматты жүйелердің орнықтылығын анқтау жүйенің сипаттамалық теңдеуін талдауға негізделген. Осы теңдеудің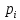
белгілі түрбірлерінде, оны былай жазуға болады:
(p-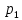 
) (p-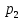
) ... (p- 
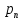) = 0. (6.68)
(6.68)-дегі р-ны jω-мен алмастырса, онда
G (jω) = a (jω -
) (jω - 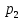) … (jω - 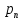) (6.69)
G (jω) сипаттамалық вектордың әр көбейткіші комплекстік сан болып табылады да, басы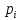
нүктесінде, ал соңы жорамал осьтегі А нүктесінде болатын вектор түрінде беріледі. ω 0-ден ∞-ке дейін өзгерген кезде, сипаттамалық векторды құрайтын векторлардың ұшы жорамал ось бойымен 
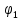аргументі өзгерте отырып ығысады. Егер түбір нақты сандар бойында жорамал осьтің сол жағында орналасса, онда ω өзгерісі кезінде векторы сағат тілінің бағытына қарсы бұрылады, оның аргументі оң, ал шекті мәні π/2-ге тең
lim arg (jω -
) = π/2
егер түбір оң жақта орналасса, онда
lim arg (jω - ) = - π/2
Ал түбірлер түйіндес, комплексті болса, онда әр түрлі векторы π/2 + γ және π/2 - γ бұрыштарына бұрылады, мұндағы γ-түбірдің координат басынан абсцисса осі бойымен жүргізілген вектормен жасайтын бұрышы. Бұл векторлар аргументінің жалпы өсімшесі 0 < ω < ∞-ке дейін өзгергенде мынаған тең болады.
π/2 + γ + π/2 - γ =π
G(jω) сипаттамалық векторы комплекс сандардың көбейтіндісі болып табылады. Оларды көбейткенде аргументтер қосылады. Демек,
arg G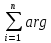(jω) =
(jω - );
0 < ω < ∞ (6.70)
Егер жорамал осьтің оң жағында «l» түбірлер орналасса, онда сол жағында (n - l) түбірлер болады, мұндағы n - теңдеулер дәрежесі. G(jω) вектордың қорытынды аргументі.
arg G(jω) = (n-2l) π/2;
0 < ω < ∞ (6.71)
Барлық түбірлері жорамал осьтің сол жағында орналасатын орнықты жүйеге сәйкес келетін G(jω) векторының шамасы мен бағыты да өзгеріп отырып, оның ұшымен қайсыбір қисық сызылады, оны Михайлов годорафы дейді. Комплексті айнымалы жазықтығында орналасатын бұл қисықтың түрі бойынша орнықты ма, жоқ па екенін анықтайды.
Михайлов қисығын салу үшін сипаттамалық теңдеуіндегі р-ның орнына jω-ны қояды.
G(jω) = (jω)n + 
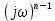+ ... = 0 (6.72)
G(jω) векторын айғақты және жорамл бөліктер түрінде көрсетеді
G(jω) = X (jω) + jY(jω), (6.73)
мұндағы
X(ω) + + 
+ 
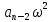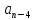
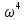- … (6.74)
Y(ω) +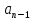
+ 
+ 
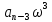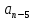
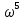- … (6.75)
ω-ға 0-ден ∞-ке дейінгі аралықта әр түрлі мәндер бере отырып, X(ω) мен Y(ω)-ның бірқатар шамасын алады, ол G(jω) векторы ұшының координаттарын білдіреді. Осы нүктелерді өзара қосу арқылы Михайлов годографын аламыз. Бұл қисық ω < кезінде әрқашан оң айғақты осьте X(ω) + , Y(ω) = 0 нүктесінде басталуы тиіс, ал (6.72) шартын сақтау үшін қисық жазықтықтың n квадрантын сағат тілінің бағытына қарсы бірітіндеп, координат басын баспай өтуі тиіс.
6.16-сурет.
Егер зерттелетін жүйе орнықсыз болса, онда бұрылыстың қорытынды бұрышы n π/2-ден кем болып, годограф n квадрантты басып өтпейді.Суретте үзік сызықпен орнықсыз жүйенің Михайлов годорафы көрсетілген, өйткені ол квадранттың бірінен (үшінщісінен) өтпейді.
6.17-сурет.
Орнықты жүйе үшін n-ші квадрантта қисық шексіздікке кетуі тиіс, өйткені тек осы жағдайда ғана (16) шарты орындалады. Сонымен, Михайлов орнықтылығының критерийі былай өрнектеледі: егер n-ші ретті АРЖ орнықты болса, онда сипаттамалық вектор ω 0-ден ∞-ке дейін өзгергенде Михайлов годографы оң айғақты жарты осьтен басталып комплексті жазықтықтың n квадранттар санын сағат тілінің бағытына қарсы қарсы кезектеп өтуі тиіс.
Мысал. Төртінші ретті сипаттамалық теңдеуі бар жүйені орнықтылыққа тексеру керек Р-ны jω-ға алмастырып
G(p) = 3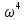 - j5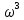 
- 8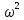
+ j 2ω + 2 = 0
алады.
Вектордың айғақты және жорамал бөлігін (18), (19) формулаларына сәйкес анықтайды.
X(ω) = 2 - 8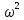 + 3 
Y(ω) = 2 ω - 5
ω-ның әр түрлі мәнін қоя отырып, X(ω) және Y(ω) анықтайды. Олардың мәндері 6.1-кестеге түсірілген.
6.1-кесте
Есептеу нәтижесі бойынша Михайлов қисығын салады. Қисық айғақты осьтің оң бөлігінде ω = 0, = 2 кезінде басталып, содан кейін, сипаттамалық теңдеудің дәрежесіне тең квадранттар санын, яғни төрт квадрантты басып өтіп, төртінші квадрантта шексіздікке кетеді. Демек, жүйе орнықты.
Найквист критерийі. Бұл критерийдің көмегімен ажыратылған жүйенің амплитудалы-фазалы-жиіліктік сипаттамсының түрі бойынша тұйықталған жүйенің орнықтылығын бағалауға болады. Осы критерий қазір оңайлығы, көрнекілігі және тәжірибе жасауға мүмкіншіліқ туғызуына байланысты кең тараған.
Найквист критерийінің көмегімен автоматты жүйенің орнықтылығын тәжірибе арқылы зерттегенде ондағы кері байланысты үзеді.Жүйенің кірісіне амплитудасы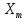
мен жиілігі ωx =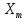 
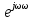тұрақты тербеліс беріледі. Сызықтық жүйе арқылы өткен сигналдың жүйенің шығысындағы жиілігі де сондай, ал амплитудасы мен фазасы өзгеше болады:
y =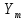
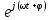
Комплекстік беріліс коэффициенті немесе жиіліктік беріліс функциясы бұлай анықталады.
Орыс ғалымы, академик А.М.Ляпунов бірінші болып орнықтылықтың дәл анықтамасын тұжырымдап қозғалыстың орнықтылығын зерттеудің жалпы әдісін жасады. Оның теориясы бойынша сызықты АРЖ-ның орнықтылығы сипаттамалық теңдеудің түбірлерімен анықталады. Сызықтық АРЖ-ның орнықтылық шартының аналитикалық тұжырымын А.М.Ляпунов былайша тұжырымдайды: сызықты АРЖ орнықты болуы үшін мынадай шарттар қажетті және жеткілікті: сипаттамалық теңдеудің барлық айғақты түбірлерінің теріс таңбалы болуы, ал комплекс түбірлерінің айғақты бөлігі теріс таңбалы болуы тиіс.
Осылайша түбірлердің комплекс жазықтығында жорамал осі орнықтылық шекарасы болып табылады. Орнықтылық шекарасындағы бейтарап жүйе үшін жорамал осьте орналасқан түбірлердің болуы ал орнықсыз жүйе үшін жорамал осьтің оң жағында екм дегенде бір түбірдің болуы қажет.
Бірінші және екінші ретті жүйелердің сипаттамалық теңдеулерінің барлық коэффиценттері нөлден үлкен болса олар орнықты келеді. Жоғары ретті жүйе үшін бұл шарт тек қажетті ғана, бірақ жеткіліксіз. АРЖ-ның орнықтылығын әдетте орнықтылық критерийлерімен бағалайды. Орнылықтылықтың негізгі Раус - Гурвиц, Михайлов және Найквист критерийлері секілді үш критерийі бар. Олар жеке-жеке қарастырайық.
6.7. Орнықтылықтың алгебралық критерийлері
Раус - Гурвиц критерийі. Кейде алгебралық деп аталатын Раус - Гурвиц критерийінің мәні былайша анықталады:
G (p) =
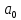
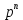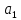
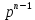+ + … + = 0. (6.62)Сипаттамалық теңдеудің түбірлері жорамал осьтің сол жағында жатып және жүйе орнықты болуы үшін Гурвицтің барлық
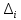диагональ минорлары сипаттамалық теңдеудің оң коэффициенттері кезінде оң болуы қажетті әрі жеткілікті. Сипаттамалық теңдеуден Гурвицтің бас анықтауышы мынаған тең: Осы анықтауышты құрағанда диагональ бойымен коэффициенттерді өспелі дәреже бойынша жазады. (6.63)-дегі үзік сызықпен таңбаланған барлық диагональ минорлары
> 0 кезінде оң болуы тиіс. Мысалы, бірінші ретті жүйе үшін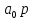 + = 0 (6.64)орнықтылық шарты
> 0; > 0.Екінші ретті жүйе үшін
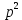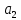+ р + = 0Қажетті және жеткілікті шарт орындалу үшін сипаттамалық теңдеудің барлық коэффициенттері оң болуы тиіс:
> 0; 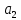> 0; >0.Үшінші ретті жүйе жүйе үшін
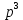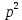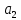+ + р +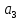 = 0 (6.66)(6.66) сипаттамалық теңдеуінің барлық коэффициенттері, оған қоса екінші ретті
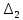және 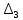анықтауыштары оң болуы қажетті әр жеткілікті.Осылайша, үшінші және төртінші ретті теңдеулер үшін коэффициенттердің оң болуынан басқа (6.66) теңсіздіктерінің орындалуы да қажет.
Михайлов критерийі. Бұл критерийді А.В. Михайлов 1936 жылы жариялаған. Ол сызықты тұйықталған автоматты реттеу жүйелерін зерттеуге арналған. Автоматты жүйелердің орнықтылығын анқтау жүйенің сипаттамалық теңдеуін талдауға негізделген. Осы теңдеудің
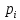белгілі түрбірлерінде, оны былай жазуға болады: (p-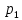
) (p-
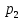) ... (p- 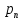) = 0. (6.68)(6.68)-дегі р-ны jω-мен алмастырса, онда
G (jω) = a (jω -
) (jω - 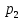) … (jω - 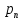) (6.69)G (jω) сипаттамалық вектордың әр көбейткіші комплекстік сан болып табылады да, басы
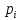нүктесінде, ал соңы жорамал осьтегі А нүктесінде болатын вектор түрінде беріледі. ω 0-ден ∞-ке дейін өзгерген кезде, сипаттамалық векторды құрайтын векторлардың ұшы жорамал ось бойымен 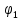аргументі өзгерте отырып ығысады. Егер түбір нақты сандар бойында жорамал осьтің сол жағында орналасса, онда ω өзгерісі кезінде векторы сағат тілінің бағытына қарсы бұрылады, оның аргументі оң, ал шекті мәні π/2-ге теңlim arg (jω -
) = π/2егер түбір оң жақта орналасса, онда
lim arg (jω -
) = - π/2Ал түбірлер түйіндес, комплексті болса, онда әр түрлі векторы π/2 + γ және π/2 - γ бұрыштарына бұрылады, мұндағы γ-түбірдің координат басынан абсцисса осі бойымен жүргізілген вектормен жасайтын бұрышы. Бұл векторлар аргументінің жалпы өсімшесі 0 < ω < ∞-ке дейін өзгергенде мынаған тең болады.
π/2 + γ + π/2 - γ =π
G(jω) сипаттамалық векторы комплекс сандардың көбейтіндісі болып табылады. Оларды көбейткенде аргументтер қосылады. Демек,
arg G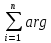(jω) =
(jω - );0 < ω < ∞ (6.70)
Егер жорамал осьтің оң жағында «l» түбірлер орналасса, онда сол жағында (n - l) түбірлер болады, мұндағы n - теңдеулер дәрежесі. G(jω) вектордың қорытынды аргументі.
arg G(jω) = (n-2l) π/2;
0 < ω < ∞ (6.71)
Барлық түбірлері жорамал осьтің сол жағында орналасатын орнықты жүйеге сәйкес келетін G(jω) векторының шамасы мен бағыты да өзгеріп отырып, оның ұшымен қайсыбір қисық сызылады, оны Михайлов годорафы дейді. Комплексті айнымалы жазықтығында орналасатын бұл қисықтың түрі бойынша орнықты ма, жоқ па екенін анықтайды.
Михайлов қисығын салу үшін сипаттамалық теңдеуіндегі р-ның орнына jω-ны қояды.
G(jω) =
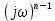(jω)n + + ... = 0 (6.72)G(jω) векторын айғақты және жорамл бөліктер түрінде көрсетеді
G(jω) = X (jω) + jY(jω), (6.73)
мұндағы
X(ω) +
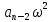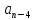
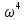+ + - … (6.74)Y(ω) +
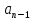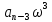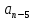
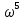+ + - … (6.75)ω-ға 0-ден ∞-ке дейінгі аралықта әр түрлі мәндер бере отырып, X(ω) мен Y(ω)-ның бірқатар шамасын алады, ол G(jω) векторы ұшының координаттарын білдіреді. Осы нүктелерді өзара қосу арқылы Михайлов годографын аламыз. Бұл қисық ω < кезінде әрқашан оң айғақты осьте X(ω) +
, Y(ω) = 0 нүктесінде басталуы тиіс, ал (6.72) шартын сақтау үшін қисық жазықтықтың n квадрантын сағат тілінің бағытына қарсы бірітіндеп, координат басын баспай өтуі тиіс.6.16-сурет.
Егер зерттелетін жүйе орнықсыз болса, онда бұрылыстың қорытынды бұрышы n π/2-ден кем болып, годограф n квадрантты басып өтпейді.Суретте үзік сызықпен орнықсыз жүйенің Михайлов годорафы көрсетілген, өйткені ол квадранттың бірінен (үшінщісінен) өтпейді.
6.17-сурет.
Орнықты жүйе үшін n-ші квадрантта қисық шексіздікке кетуі тиіс, өйткені тек осы жағдайда ғана (16) шарты орындалады. Сонымен, Михайлов орнықтылығының критерийі былай өрнектеледі: егер n-ші ретті АРЖ орнықты болса, онда сипаттамалық вектор ω 0-ден ∞-ке дейін өзгергенде Михайлов годографы оң айғақты жарты осьтен басталып комплексті жазықтықтың n квадранттар санын сағат тілінің бағытына қарсы қарсы кезектеп өтуі тиіс.
Мысал. Төртінші ретті сипаттамалық теңдеуі бар жүйені орнықтылыққа тексеру керек Р-ны jω-ға алмастырып
G(p) = 3
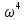- j5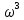
- 8
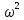+ j 2ω + 2 = 0алады.
Вектордың айғақты және жорамал бөлігін (18), (19) формулаларына сәйкес анықтайды.
X(ω) = 2 - 8
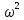+ 3 Y(ω) = 2 ω - 5
ω-ның әр түрлі мәнін қоя отырып, X(ω) және Y(ω) анықтайды. Олардың мәндері 6.1-кестеге түсірілген.
6.1-кесте
| ω, 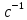 | 0 | 0,3 | 0,5 | 1,0 | 2,0 | 10 |
| X(ω) | 2 | 1,3 | 0,18 | -3 | 18 | 29202 |
| Y(ω) | 0 | 0,465 | 0,375 | -3 | -36 | -4980 |
Есептеу нәтижесі бойынша Михайлов қисығын салады. Қисық айғақты осьтің оң бөлігінде ω = 0,
= 2 кезінде басталып, содан кейін, сипаттамалық теңдеудің дәрежесіне тең квадранттар санын, яғни төрт квадрантты басып өтіп, төртінші квадрантта шексіздікке кетеді. Демек, жүйе орнықты.Найквист критерийі. Бұл критерийдің көмегімен ажыратылған жүйенің амплитудалы-фазалы-жиіліктік сипаттамсының түрі бойынша тұйықталған жүйенің орнықтылығын бағалауға болады. Осы критерий қазір оңайлығы, көрнекілігі және тәжірибе жасауға мүмкіншіліқ туғызуына байланысты кең тараған.
Найквист критерийінің көмегімен автоматты жүйенің орнықтылығын тәжірибе арқылы зерттегенде ондағы кері байланысты үзеді.Жүйенің кірісіне амплитудасы
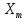мен жиілігі ωx =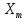 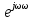тұрақты тербеліс беріледі. Сызықтық жүйе арқылы өткен сигналдың жүйенің шығысындағы жиілігі де сондай, ал амплитудасы мен фазасы өзгеше болады:y =
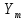
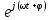
Комплекстік беріліс коэффициенті немесе жиіліктік беріліс функциясы бұлай анықталады.