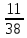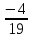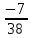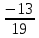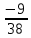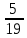ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оптимальный план можно записать так:
y1 = 0, y2 = 3/38, y3 = 1/38
Z(Y) = 1*0 + 1*3/38 + 1*1/38 = 2/19
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
x1=1/19, x2=0, x3=1/19
Это же решение можно получить, применив теоремы двойственности.
Из теоремы двойственности следует, что X = C*A-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
| A = (A2, A5, A3) = |
|
Определив обратную матрицу D = А-1 через алгебраические дополнения, получим:
| D = A-1 = |
|
Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных.
Оптимальный план двойственной задачи равен:
x1 = 1/19, x2 = 0, x3 = 1/19
F(X) = 1*1/19+1*0+1*1/19 = 2/19
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
qi = g*yi; pi = g*xi.
Цена игры: g = 1 : 2/19 = 19/2
p1 = 19/2*1/19 = 1/2
p2 = 19/2*0 = 0
p3 = 19/2*1/19 = 1/2
Оптимальная смешанная стратегия игрока I: P = (1/2; 0; 1/2)
q1 = 19/2*0 = 0
q2 = 19/2*3/38 = 3/4
q3 = 19/2*1/38 = 1/4
Оптимальная смешанная стратегия игрока II: Q = (0; 3/4; 1/4)
Цена игры: v=19/2
Задание 4
Платежная матрица игрока МА:
| -5 | -4 |
| 4 | -13 |
Позиции максимумов в столбцах матрицы МА: (2,1), (1,2)
Платежная матрица игрока МB:
| -3 | -4 |
| 4 | 5 |
Позиции максимумов в строках матрицы МВ: (1,1), (2,2)
C = -5 - (-4) - 4 -13 = -18
α = -13 - (-4) = -9
D = -3 - (-4) - 4 + 5 = 2
β = 5 - 4 = 1
(p–1)(-18q+9) ≥ 0
p(-18q+9) ≥ 0
(q-1)(2p-1) ≥ 0
q(2p-1) ≥ 0
получаем, что:
1) p=1,q ≤ 1/2
p=0, q ≥ 1/2
0 ≤ p ≤ 1, q=1/2
2) q=1,p ≥ 1/2
q=0, p ≤ 1/2
0 ≤ q ≤ 1, p=1/2
Рассматриваемая игра имеет единственную ситуацию равновесия (P*,Q*), где оптимальными стратегиями по Нэшу являются:
P* = (1/2;1/2); Q* = (1/2;1/2).
Она может быть реализована при многократном повторении игры (то есть при многократном воспроизведении описанной ситуации) следующим образом:
игрок I должен использовать чистые стратегии 1 и 2 с частотами 1/2 и 1/2, а игрок II – чистые стратегии 1 и 2 с частотами
1/2 и 1/2. Любой из игроков,
отклонившись от указанной смешанной стратегии, уменьшает свой ожидаемый выигрыш.
Цена игры
Цена игры для первого игрока:
Ha(1/2;1/2) = -9/2
Цена игры для второго игрока:
Hb(1/2;1/2) = 1/2
Ответ:
Смешанная стратегия для первого игрока P* = (1/2;1/2); Смешанная стратегия для второго игрока Q* = (1/2;1/2).
Выигрыш игроков в равновесной ситуации:
f(P*,Q*) = (-9/2;1/2).