ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 73
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Графическое решение
Возьмем участок оси абсцисс единичной длины и проведем через его концы вертикальные прямые a1 и a2 соответствующие нашим стратегиям A1 и A2. Предположим теперь, что игрок "B" будет пользоваться стратегией B1 в чистом виде. Тогда, если игрок "A" будет использовать чистую стратегию A1, то выигрыш составит 4.Отметим соответствующую ему точку на оси a1.
Если будет использовать чистую стратегию A2, то наш выигрыш составит 11. Отметим соответствующую ему точку на оси a2
Если будем применять, смешивая в различных пропорциях стратегии A1 и A2, выигрыш будет меняться по прямой проходящей через точки с координатами (0 , 4) и (1 , 11), назовем ее линией стратегии B1 (на Рис.1 показана красным цветом). Абсцисса любой точки на данной прямой равна вероятности p2 (частоте), с которой мы применяем стратегию A2, а ордината - получаемому при этом выигрышу k (см. Рис.1).
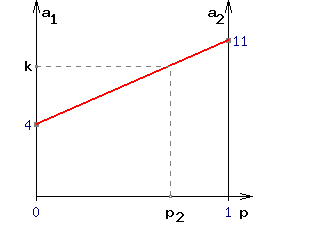
Рисунок 1.
График зависимости выигрыша k от частоты р2, при использовании противником стратегии B1.
игрок "B" будет пользоваться стратегией B3 в чистом виде. Тогда, если игрок "A" будет использовать чистую стратегию A1, то выигрыш составит 8.Если будет использовать чистую стратегию A2, то выигрыш составит -1 (см. Рис. 2). Аналогично, если будем смешивать в различных пропорциях стратегии A1 и A2, наш выигрыш будет меняться по прямой проходящей через точки с координатами (0 , 8) и (1 , -1), назовем ее линией стратегии B3
Абсцисса любой точки на этой прямой равна вероятности, с которой мы применяем стратегию A2, а ордината - получаемому при этом выигрышу, но только для стратегии B3 (см. Рис. 2).
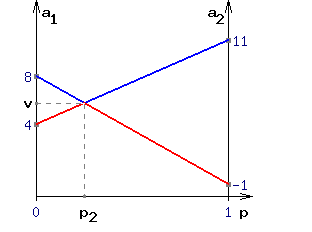
Рисунок 2.
Графическое определение цены игры v и оптимальной частоты р2 для игрока "А".
Самая высокая точка этой ломанной соответствует нашей оптимальной стратегии. В данном случае, это точка пересечения линий стратегий B
1 и B3.
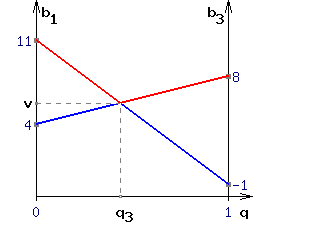
Рисунок 3.
Графическое определение цены игры v и оптимальной частоты q3 для игрока "В".
Значение частоты q1, это длина отрезка [q3 ; 1] на оси абсцисс.
Задание 2
Исходные данные:
| 13 | 12.5 | 13.1 | 12 |
| 12.2 | 13.6 | 11.9 | 12.3 |
| 11.6 | 12.1 | 12.8 | 12 |
| 11.5 | 11.9 | 11.9 | 11.8 |
Критерий Байеса.
По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(aijpj)
∑(a1,jpj) = 13*0.7 + 12.5*0.7 + 13.1*0.7 + 12*0.7 = 35.42
∑(a2,jpj) = 12.2*0.7 + 13.6*0.7 + 11.9*0.7 + 12.3*0.7 = 35
∑(a3,jpj) = 11.6*0.7 + 12.1*0.7 + 12.8*0.7 + 12*0.7 = 33.95
∑(a4,jpj) = 11.5*0.7 + 11.9*0.7 + 11.9*0.7 + 11.8*0.7 = 32.97
| Ai | П1 | П2 | П3 | П4 | ∑(aijpj) |
| A1 | 9.1 | 8.75 | 9.17 | 8.4 | 35.42 |
| A2 | 8.54 | 9.52 | 8.33 | 8.61 | 35 |
| A3 | 8.12 | 8.47 | 8.96 | 8.4 | 33.95 |
| A4 | 8.05 | 8.33 | 8.33 | 8.26 | 32.97 |
| pj | 0.7 | 0.7 | 0.7 | 0.7 | |
Выбираем из (35.42; 35; 33.95; 32.97) максимальный элемент max=35.42
Вывод: выбираем стратегию N=1.
Критерий Лапласа.
Если вероятности состояний природы правдоподобны, для их оценки используют
принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.:
q1 = q2 = ... = qn = 1/n.
qi = 1/4
| Ai | П1 | П2 | П3 | П4 | ∑(aij) |
| A1 | 3.25 | 3.125 | 3.275 | 3 | 12.65 |
| A2 | 3.05 | 3.4 | 2.975 | 3.075 | 12.5 |
| A3 | 2.9 | 3.025 | 3.2 | 3 | 12.125 |
| A4 | 2.875 | 2.975 | 2.975 | 2.95 | 11.775 |
| pj | 0.25 | 0.25 | 0.25 | 0.25 | |
Выбираем из (12.65; 12.5; 12.13; 11.78) максимальный элемент max=12.65
Вывод: выбираем стратегию N=1.
Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min aij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
| Ai | П1 | П2 | П3 | П4 | min(aij) |
| A1 | 13 | 12.5 | 13.1 | 12 | 12 |
| A2 | 12.2 | 13.6 | 11.9 | 12.3 | 11.9 |
| A3 | 11.6 | 12.1 | 12.8 | 12 | 11.6 |
| A4 | 11.5 | 11.9 | 11.9 | 11.8 | 11.5 |
Выбираем из (12; 11.9; 11.6; 11.5) максимальный элемент max=12
Вывод: выбираем стратегию N=1.
Критерий Гурвица.
Рассчитываем si.
s1 = 0.7*12+(1-0.7)*13.1 = 12.33
s2 = 0.7*11.9+(1-0.7)*13.6 = 12.41
s3 = 0.7*11.6+(1-0.7)*12.8 = 11.96
s4 = 0.7*11.5+(1-0.7)*11.9 = 11.62
| Ai | П1 | П2 | П3 | П4 | min(aij) | max(aij) | y min(aij) + (1-y)max(aij) |
| A1 | 13 | 12.5 | 13.1 | 12 | 12 | 13.1 | 12.33 |
| A2 | 12.2 | 13.6 | 11.9 | 12.3 | 11.9 | 13.6 | 12.41 |
| A3 | 11.6 | 12.1 | 12.8 | 12 | 11.6 | 12.8 | 11.96 |
| A4 | 11.5 | 11.9 | 11.9 | 11.8 | 11.5 | 11.9 | 11.62 |
Выбираем из (12.33; 12.41; 11.96; 11.62) максимальный элемент max=12.41
Вывод: выбираем стратегию N=2.
Критерий Ходжа-Лемана.
Для каждой строки рассчитываем значение критерия по формуле:
Wi = u∑aijpj + (1 - u)min(a)ij
Рассчитываем Wi.
W1 = 0.7*35.42 + (1-0.7)*12 = 28.394
W2 = 0.7*35 + (1-0.7)*11.9 = 28.07
W3 = 0.7*33.95 + (1-0.7)*11.6 = 27.245
W4 = 0.7*32.97 + (1-0.7)*11.5 = 26.529
| Ai | П1 | П2 | П3 | П4 | ∑(aijpj) | min(aj) | Wi |
| A1 | 9.1 | 8.75 | 9.17 | 8.4 | 35.42 | | 28.394 |
| A2 | 8.54 | 9.52 | 8.33 | 8.61 | 35 | | 28.07 |
| A3 | 8.12 | 8.47 | 8.96 | 8.4 | 33.95 | | 27.245 |
| A4 | 8.05 | 8.33 | 8.33 | 8.26 | 32.97 | | 26.529 |
| pj | 0.7 | 0.7 | 0.7 | 0.7 | | | |
Выбираем из (28.39; 28.07; 27.25; 26.53) максимальный элемент max=28.39
Вывод: выбираем стратегию N=1.
Обобщенный критерий Гурвица.
Подход пессимиста. λ выбирается из условия невозрастания среднего:
G1 = 0.478*12+(1-0.478)*13.1 = 12.575; G2 = 0.478*11.9+(1-0.478)*13.6 = 12.788; G3 = 0.478*11.6+(1-0.478)*12.8 = 12.227; G4 = 0.478*11.5+(1-0.478)*11.9 = 11.709;
Подход оптимиста. λ выбирается из условия неубывания среднего:
G1 = 0.522*12+(1-0.522)*13.1 = 12.525; G2 = 0.522*11.9+(1-0.522)*13.6 = 12.712; G3 = 0.522*11.6+(1-0.522)*12.8 = 12.173; G4 = 0.522*11.5+(1-0.522)*11.9 = 11.691;
| Ai | П1 | П2 | П3 | П4 | min(aij) | max(aij) | Подход пессимиста | Подход оптимиста |
| A1 | 12 | 12.5 | 13 | 13.1 | 12 | 13.1 | 12.574593495935 | |
| A2 | 11.9 | 12.2 | 12.3 | 13.6 | 11.9 | 13.6 | 12.788008130081 | |
| A3 | 11.6 | 12 | 12.1 | 12.8 | 11.6 | 12.8 | 12.226829268293 | |
| A4 | 11.5 | 11.8 | 11.9 | 11.9 | 11.5 | 11.9 | 11.708943089431 | |
Выбираем из (12.575; 12.788; 12.227; 11.709) максимальный элемент max=12.79
Вывод: выбираем стратегию N=2.
Оптимальные стратегии по обобщенному критерию Гурвица.
b = 47 + 48.5 + 49.3 + 51.4 = 196.2
Показатели эффективности по Гурвицу.
Подход пессимиста