Вычислим критерий Фишера:

при двух степенях свободы:

По статистическим таблицам находим критическое значение критерия

Фишера для рекомендуемого уровня значимости α=0.05 Так как вычисленное значение критерия Фишера превосходит критическое, то будем считать уровень значимости по критерию Фишера удовлетворительным.

Вычислим коэффициент множественной детерминации:

для двух степеней свободы



По статистической таблице для уровня значимости 0,05 находим критическое значение коэффициента множественной детерминации:

Так как вычисленное значение коэффициента множественной детерминации превышает критическое значениe, то полученный результат по данному показателю будем считать удовлетворительным.

Таким образом, все полученные расчётные показатели по оценке качества уравнения регрессии являются удовлетворительными, поэтому будем считать результаты аппроксимации приемлемыми.
Задание 1.4

Пример 1.4.1

Провести оптимизацию графическим методом.





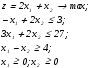
Приравняем целевую функцию нулю, неравенства заменим равенствами и затем представим их функциями х₂отх₁.

х₂=-2х₁;

х₂= 1,5+0,5х₁;

х₂=13,5-1,5х₁;

х₂=-4+х₁

и представим в системе координат на рис.4.1.

у (2)

---

9

8

1. 
   (3)
   

6
4

2

ОДР



1 2 3 4 5 6 7 8 9 х

Целевая функция



Рис.4.1

Область допустимых решений (ОДР) ограничивается осью координат х₁,

ограничением (2) и ограничением (3). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (4;0) а последняя – максимума (9;0). В точке минимума z =8,в точке максимума z=18. Проверим выполнение всех ограничений в найденных точках.

Для точки минимума

-4+0<3 выполняется;

3·4+0<27 выполняется;

4-0=4 выполняется как равенство.

Для точки максимума

-9+0<3 выполняется;

3·9+0=27 выполняется как равенство

---

;

9-0>4 выполняется.

Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным.

Отметим, что если какая-то проверяемая точка превращает неравенство в равенство, то данная точка принадлежит прямой линии, представляющей данное неравенство. В процессе оптимизации может оказаться, что какая-то точка лежит на пересечении двух, или большего количества прямых, то её координаты можно найти решением системы уравнений.

Пример 1.4.2

Если в условиях примера 1.4.1 изменить третье неравенство на х₁+х₂≤4 то постановка задачи примет следующий вид:



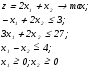
В этом случае произойдёт перемещение области допустимых решений как это показано на рис.4.2.

у (2)

9

8

1. 
   (3)
   

6
4

---

2 ОДР

ОДР



1 2 3 4 5 6 7 8 9 х

Целевая функция



Рис.4.2

Область допустимых решений (ОДР) ограничивается осью координат х₁ и тремя ограничениями (1), (2) и (3). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (0;0) а последняя – точкой максимума (7;3). В точке минимума z =0,в точке максимума z=17. Проверим выполнение всех ограничений в найденных точках.

Для точки минимума

-0+0<3 выполняется;

0+0<27 выполняется;

0-0<4 выполняется.

Для точки максимума

-7+2·3<3 выполняется;

3·7+2·3=27 выполняется как равенство;

7-3=4 выполняется как равенство.

Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным.

Отметим, что если какая-то проверяемая точка превращает неравенство в равенство, то данная точка принадлежит прямой линии, представляющей данное неравенство. В процессе оптимизации может оказаться, что какая-то точка лежит на пересечении двух, или большего количества прямых, то её координаты можно найти решением системы уравнений. В нашем случае точка максимума лежит на пересечении ограничений (2) и (3). Покажем, что в данном случае её координаты можно найти решением уравнения

х₂=13,5-1,5·х₁=-4+х₁;

откуда 2,5·х₁=17,5; х₁=17,5/2,5=7;

х₂=-4+7=3.

Пример 1.4.3

В условиях примера 1.4.2 произведём преобразование, изменив ограничение (2). Тогда постановка задачи оптимизации примет следующий вид:



В этом случае произойдёт перемещение области допустимых решений как это показано на рис.4.3.

у (2)

---

9

8 (3)



6 (1)




4 ОДР



2



1 2 3 4 5 6 7 8 9 10 11 х

Целевая функция



Рис.4.3

Область допустимых решений (ОДР) определяется тремя ограничениями (1), (2) и (3). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (6;4,5) а последняя – точкой максимума (11;7). В точке минимума z =16,5,в точке максимума z=28. Проверим выполнение всех ограничений в найденных точках.

Для точки минимума

-6+2·45=3 выполняется как равенство;

3·6+2·4,5=27 выполняется как равенство;

6-4.5<4 выполняется.

Для точки максимума

-11+2·7=3 выполняется как равенство;

3·11+2·7>27 выполняется;

11-7=4 выполняется как равенство.

Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным.

---

Смотрите также файлы

• Дисциплина Безопасность жизнедеятельности Раздел Теоретические основы безопасности жизнедеятельности Тема Объект, предмет, методология, теория и практика безопасности.doc

• Задание Решите ситуационную задачу, используя предложенную методику.docx

• Тесты для воспитателей и родителей Подобрать и апробировать формы и содержание работы по привлечению родителей к деятельности доу.docx

• Самозащита гражданских прав и меры оперативного воздействия как способы защиты гражданских прав.docx

• Котлекарь кот может безошибочно определить, где у хозяина больное место. Он ложится прямо на больной сустав и начинает его лечить. И ведь действительно помогает. Объясните, что за странное чутье и лекарские способности у котов Ответ.docx