ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 305
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 1 2 3 4 5 6 7 8 9 x
Рис.2.1
Вычислим значение критерия согласия Пирсона (КС c2 ) и по статистическим таблицам определим коэффициент доверия, выдвинутой гипотезе:
c2 ={(5-10)2+(10-10)2+(8-10)2+(10-10)2+(11-10)2+(9-10)2+(13-10)2+(10-10)2++(16-10)2+(8-10)2}/10={25+0+4+0+1+1+9+0+36+4}/10=8,0 приR=7.
По статистической таблице 2.1 находим коэффициент доверия Рр=0,40. Ввиду того, что вычисленное значение КС укладывается в рекомендуемый десяти процентный доверительный интервал делаем заключение что имеющиеся статистические данные не противоречат гипотезе о их подчинении равномерному закону. В таблице 2.1 жирным цветом выделены значения,
c2 при которых гипотеза о подчинении исходных случайных чисел равномерному закону не отвергается, т.е. соблюдается условие: 0.1≤рр≤0.9.
Таблица 2.1
| рр | 0.990 | 0.980 | 0.950 | 0.900 | 0.800 |
| c2 | 1.239 | 1.501 | 2.170 | 2.830 | 3.820 |
| рр | 0.700 | 0.500 | 0.300 | 0.200 | 0.100 |
| c2 | 4.670 | 6.350 | 8.380 | 9.800 | 12.02 |
| рр | 0.050 | 0.020 | 0.010 | 0.001 | 0.000 |
| c2 | 14.07 | 16.62 | 18.48 | 24.30 | ∞ |
Задание 1.3
Провести аппроксимацию пяти пар случайных чисел, представленных в таблице 3.1, линейной зависимостью
.Таблица 3.1
-
х
у
1
1
2
2
3
4
4
7
5
9
Экспериментальные точки, координаты которых представлены в таблице 3.1, представим в системе координат на рис.3.1.
у
9 •
7 • 4 • 2 •
1 •
1 2 3 4 5 х Рис.3.1
Для проведения аппроксимации проведём предварительные вычисления.
Вычислим коэффициент линейной корреляции.
По статистическим таблицам найдём критическое значение критерия Стьюдента tкрит=3,1814 при n-2=5-2=3 степенях свободы и рекомендуемому уровню значимости α=0,05.
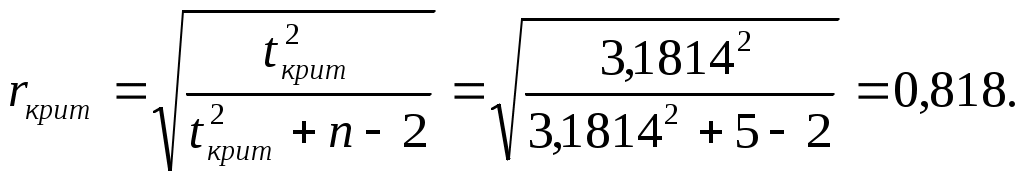
Ввиду того, что
делаем заключение, что корреляционная связь между переменными х и у является существенной и она может быть линейной.Вычислим коэффициенты линейной зависимости по формулам:
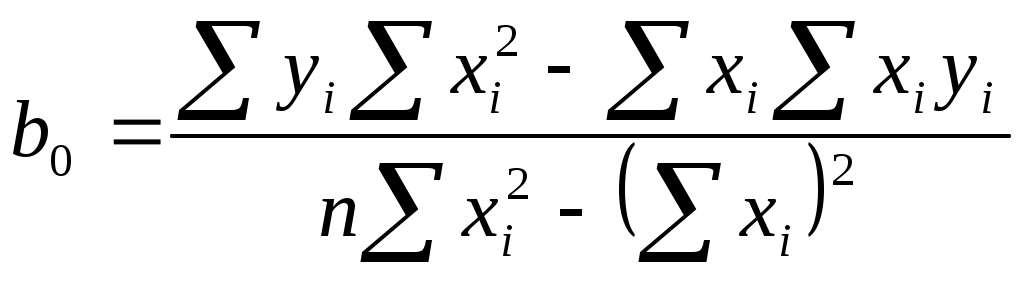
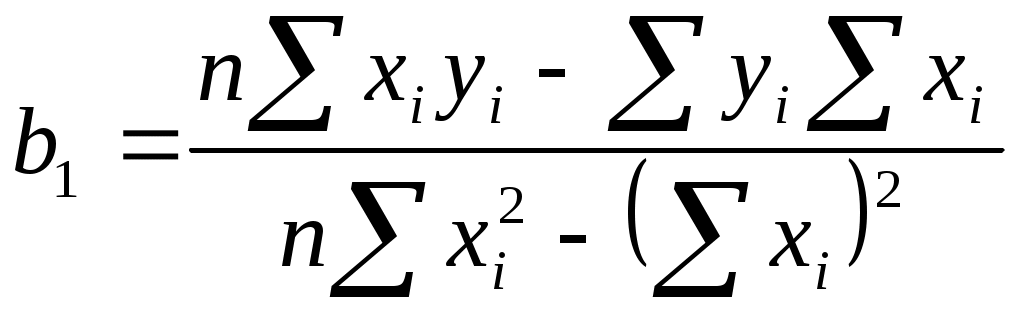
Таким образом, получили линейное уравнение регрессии:
По уравнению регрессии по двум точкам построим функцию в системе координат на рис.3.1 и вычислим значения функции по экспериментальным значениям аргумента х и разницу между экспериментальными и вычисленными значениями функции, которые представим в таблице 3.2.
Таблица 3.2
| хi | yi |  |  |  |
| 1 | 1 | 0,4 | 0,6 | 0,36 |
| 2 | 2 | 2.5 | -0,5 | 0,25 |
| 3 | 4 | 4,6 | -0,6 | 0,36 |
| 4 | 7 | 6,7 | 0,3 | 0,09 |
| 5 | 9 | 8,8 | 0,2 | 0,04 |
Вычислим стандартную ошибку и отношение стандартной ошибки к среднему значению:
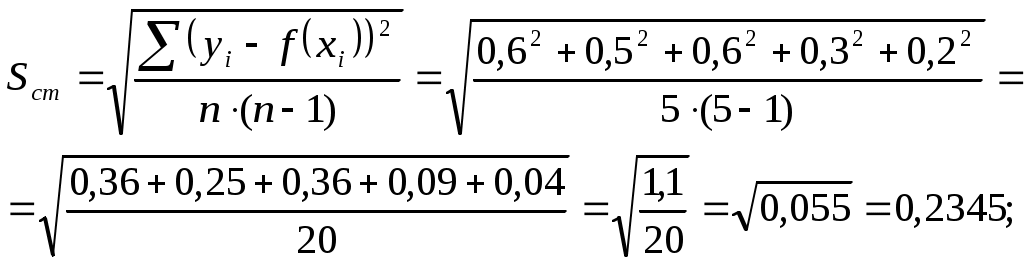
По отношению стандартной ошибки к среднему значению получен удовлетворительный результат
, так как не превышено значение в 0.05.
Проведём оценку уровня значимости коэффициентов уравнения регрессии по критерию Стьюдента:
где
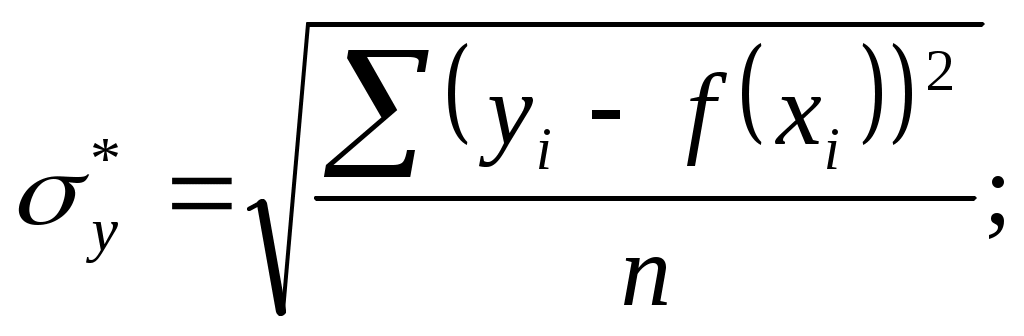
По статистической таблице находим критическое значение критерия Стьюдента tкрит=3,183 для
3 степеней свободы и рекомендуемого уровня значимости 
=0,05. Отметим, что по уровню значимости для коэффици-ентов 
и 
получен удовлетворительный результат, так как они по асолютному значению превышают критическое значение.Проведём оценку качества полученного уравнения регрессии по показателям, вычисляемым на основе дисперсионного анализа:
Проверка:
Результат проверки – положительный, что свидетельствует о корректности проведённых вычислений.