Файл: 1. интерференция света основные формулы и законы.doc

4.26. Запишите стационарное уравнение Шредингера для свободной частицы, которая движется вдоль оси , а также определите посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы?

А.[ , спектр непрерывный] В.[ , спектр дискретный]

С.[ , спектр дискретный] D.[ ,спектр дискретный]

4.27. Электрон в бесконечно глубоком одномерном прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения электрона в средней трети ящика?

А. [0,609] В. [0,5] С. [0,195] D. [0,091]

4.28. Волновая функция описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной . Вычислите вероятность нахождения частицы в малом интервале ∆ = 0,2 в двух случаях: 1) вблизи стенки ; 2) в средней части ящика .

А. [0,052; 0,4] В. [0,026; 0,2] С. [0,1; 0,4] D. [0,052; 0,8]

4.29. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной . Вычислите наименьшую разность энергий двух соседних энергетических уровней
(в электронвольтах) электрона в двух случаях: 1) = 1 мкм; 2)

---

= 0,1 нм.

A. [1,1∙10^-12 эВ; 110 эВ] В. [1,1∙10^-16 эВ; 1,1 эВ]

C. [0,55∙10^-13 эВ; 55 эВ] D. [5,5∙10^-12 эВ; 1,1 эВ]

4.30. Вероятность обнаружить частицу на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле . Если - функция имеет вид, указанный на рисунке справа, то вероятность обнаружить частицу на участке , где – ширина ящика, равна: A. [2/3] В. [1/3] С. [4/3] D. [5/6].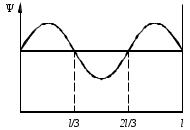

4.31. Пучок электронов с энергией Е = 15 эВ встречает на своем пути потенциальный барьер высотой U = 20 В и шириной = 0,1 нм. Определите коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1).

A. [D = 0,1; R = 0,9] В. [D = 0,9; R = 0,1]

С. [D = 0,5; R = 0,5] D. [D = 0,2; R = 0,8]

4.32. Частица массой m движется в одномерном потенциальном поле = (гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид , где – нормировочный коэффициент; - положительная постоянная. Используя уравнение Шредингера, определите:
1) постоянную ; 2) энергию частицы в этом состоянии.

А. [ ;

---

] В. [ ; ]

С. [ ; ] D. [ ; ]

4.33. Покажите, что при kT >> E_i (малом параметре вырождения) квантовые распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла – Больцмана, то есть бозонный и фермионный газы приобретают свойства классического идеального газа.

А. [ << 1; ]

4.34. Для каких квантовых частиц характерна знаковая неоднозначность волновой функции и какие значения спина имеют эти частицы?

А. [фермионов; имеют полуцелые значения спина]

В. [бозонов; имеют целые значения спина]

4.35. Для каких квантовых частиц характерна знаковая однозначность волновой функции и какие значения спина имеют эти частицы?

А. [бозонов; имеют целочисленные значения спина]

В. [фермионов; имеют полуцелочисленные значения спина]
4.3. Квантовые свойства атомов, молекул и твердых тел
Основные формулы и законы

• 
  Волновые функции связанных состояний (Е < 0) атома водорода имеют вид:
  

,

где n – главное квантовое число (n = 1, 2, 3, …), – орбитальное (азимутальное) квантовое число ( = 0, 1, 2, …, (n – 1)), m – магнитное квантовое число (m = 0, ±1, ±2, …, ± ), - радиальные функции, а

---

- сферические функции.

Квантовые числа n, , m являются характеристиками микросостояния частицы, в том числе и электрона в атоме водорода, и появляются при решении нерелятивистского уравнения Шредингера.

• 
  Квантовое магнитное спиновое число m_s (m_s=±1/2) электрона появляется лишь при решении релятивистского уравнения Дирака, т. е. спин является релятивистской характеристикой.
  
• 
  Принцип Паули: в атоме два электрона не могут находиться в одном и том же квантовом состоянии (определяемом набором четырех квантовых чисел n, ,m, m_s).
  
• 
  Электронная конфигурация атома в основном состоянии 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰…, где числа (n = 1, 2, 3, …) соответствуют главному квантовому числу, которое задает электронные слои (оболочки) K, L, M, N, …, а буквы латинского алфавита s, p, d, f соответствуют орбитальному квантовому числу ( = 0, 1, 2, 3), которое задает s, p, d, f - состояния (электронные подоболочки) атома, числа над s, p, d, f соответствуют числу электронов в соответствующих состояниях.
  
• 
  Закон Мозли
  

,

где – характеристические частоты спектра; R=3,29∙10¹⁵1/с – постоянная Ридберга; z – заряд ядра атома в относительных единицах;
σ - постоянная экранирования; m и n – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.

• 
  При σ=0 формула закона Мозли обращается в формулу, описывающую линейчатые спектры водородоподобных атомов
  

---

.

При σ = 0 и z = 1 формула закона Мозли совпадает с обобщенной формулой Бальмера для линейчатого спектра атома водорода.

• 
  Частоты излученного или поглощенного электромагнитного кванта молекулярного спектра
  

= (∆ W_эл. + ∆ W_кол. + ∆ W_вр.),

где ∆W_эл., ∆W_кол. и ∆W_вр. – разности энергий двух соответственно электронных, колебательных и вращательных уровней.

• 
  Средняя энергия квантового одномерного осциллятора
  

,

где - нулевая энергия; - постоянная Планка; - круговая частота колебаний осциллятора; k – постоянная Больцмана; T – термодинамическая температура.

• 
  Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов
  

,

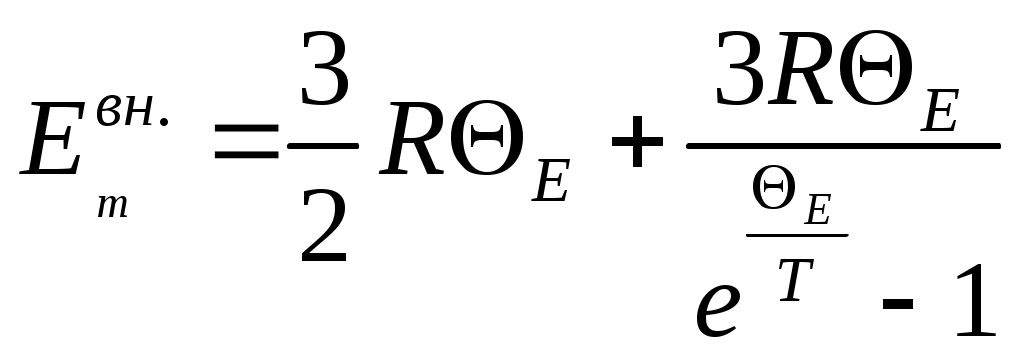где – молярная газовая постоянная; = – характеристическая температура Эйнштейна.

• 
  Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая)
  

( T << ),

где =

---