Файл: Конспект лекций Дисциплина Статистика.doc

3. Понятие вариации.

Различия индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака.

Это изменение возникает в результате того, что индивидуальные значения складываются по совокупным факторам, которые по-разному действуют на совокупность целого.

Средняя величина – это абстрактная обобщающая характеристика признака изучаемой совокупности.

Она не дает данные о том, как отдельные значения изучаемой совокупности группируются вокруг средней.

Колеблимость отдельных значений характеризуют показатели вариации. Термин «вариация» происходит от латинского и обозначает – изменения, колеблимость.

Под вариацией в статистике понимают такие количественные изменения в пределах одного признака в однородной совокупности, которые обусловлены и зависят от влияния различных факторов.

Анализ статистической совокупности позволяет оценить степень зависимости изучаемой совокупности и ее признаков от ее факторов.
Пример.
Изучая вариацию можно определить однородность совокупности. Степень близости данных отдельных единиц x к средней измеряются рядом абсолютных, относительных и средних показателей вариации.


4. Показатели вариации.

Несгрупированый ряд Сгруппированный ряд

1-й показатель-размах вариацииотклонение максимального признака от минимального
2-й показатель – среднее линейное отклонение – представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их среднего значения.
- это абсолютное значение (модель) отклонения значения варианты от ее ср. величины.
3-ий показатель – дисперсия – представляет собой средний квадрат отклонений вариант от их среднего значения.
4-ый показатель – седнее квадратическое отклонение – представляет собой корень из дисперсии.

---

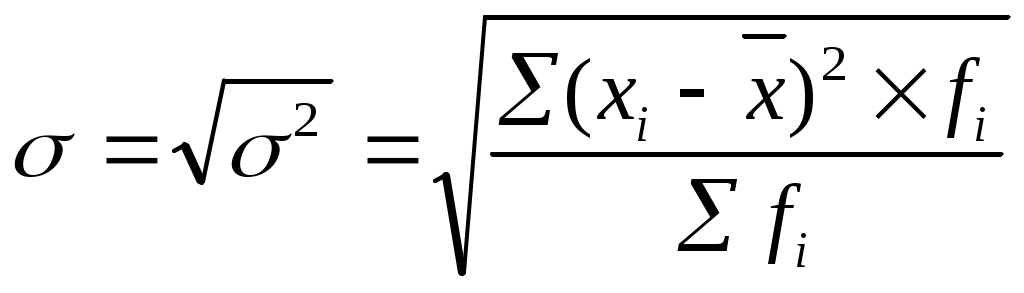5-ый показатель. Коэффициент вариации – это отношение седнего квадратического отклонения к среднему значению.


Коэффициент вариации применяется в следующих случаях:

• 
  когда необходимо определить и сравнить степени рассеивания 2-х или нескольких признаков, выраженных в различных единицах измерения для характеристики одной и той же совокупности;
  

• 
  когда необходимо определить рассеивание одного и того же признака в разных единицах совокупности, имеющих разные единицы измерений и разные ср. величины.
  

Если коэффициент вариации составляет более 0,40 то такая совокупность считается неоднородной.
Пример.
Имеются данные о стаже работы рабочих 3-х бригад:
I бригада – 15, 18, 20, 22, 25 лет;

II бригада – 10, 15, 20, 25, 30 лет;

III бригада – 8, 12, 17, 25, 38 лет.
Определить показатель вариации.
1. Размах вариации.

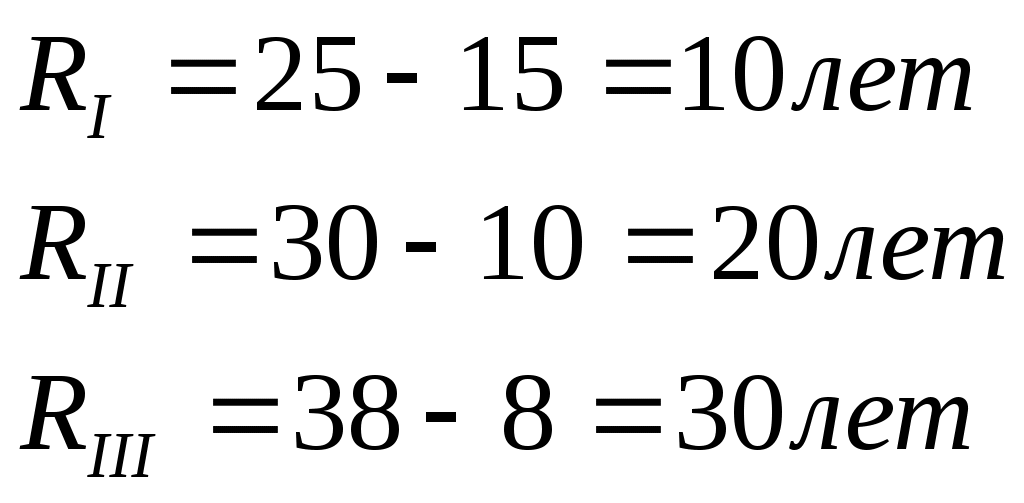
2. Среднее линейное отклонение.
I.
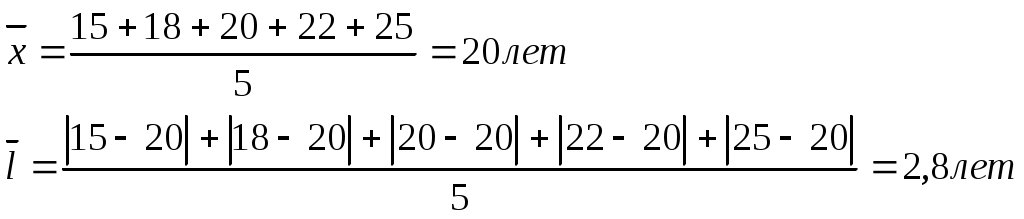
II.
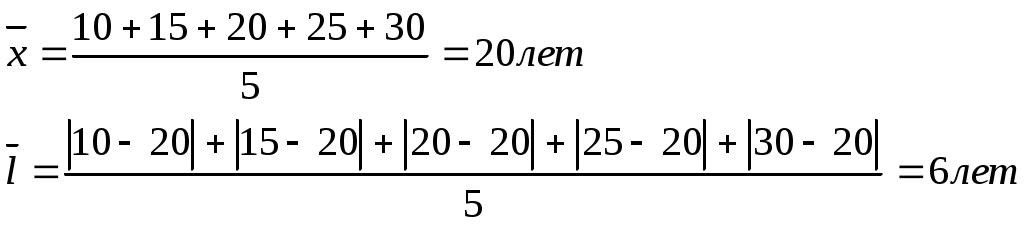
III.

В I бригаде абсолютное отклонение каждого значения от средней величины 2,8 лет, во II бригаде – 6 лет, в III бригаде – 9,2 лет.


3. Дисперсия, средний квадрат отклонения.

I.
II.
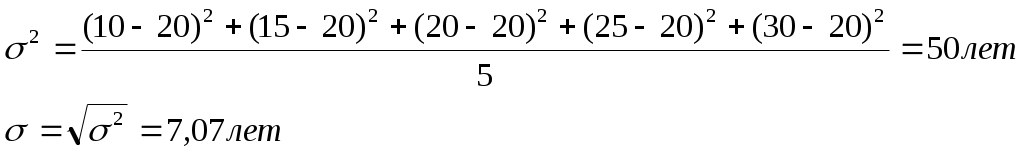
III.

Чем больше ср. квадратическое отклонение, тем более высока вариация, т.е. более неточным будет среднее значение.
4. Коэффициент вариации.

I.
II.
III.
III бригада является неоднородной совокупностью, т.к. коэффициент вариации составляет более 0,40.

5. Показатели относительного рассеивания.

---

Данные показатели позволяют охарактеризовать совокупность, а в частности колеблимость изучаемого признака. Показатели относительного рассеивания определяются путем деления меры относительного рассеивания на среднюю арифметическую величину и выражаются в %. К таким показателям относятся:
1). Коэффициент осцеляции – определяется как отношение размаха вариации к средней величине признака и характеризует относительную рассеянность или колеблимость крайних значений признака вокруг средней:
,

где – размах вариации. Этот показатель показывает на сколько % отклоняется среднее от крайних значений вариации.

Если >100, то (крайних значений признака) и наоборот.
2). Относительное линейное отклонение.-средние линейное отклонение делим на среднюю величину, ия:


Пример.
Рассчитать показатели вариации и показатели относительного рассеивания по данным таблицы.

Выполнение нормы	Среднее значение	Численность рабочих, чел.
80-90	85	5
90-100	95	19
100-110	105	36
110-120	115	25
120 и более	125	15 / 100

6. Закон сложения дисперсии.
Если статистическая совокупность разбита на несколько групп по одинаковому признаку, то средняя величина и дисперсия могут быть определены не только для всей совокупности, но и для отдельной ее части. В зависимости от этого можно выделить межгрупповую и внутригрупповую вариацию. А, следовательно, рассчитать среднюю величину и дисперсию, как межгрупповую, так и внутригрупповую.

---

В зависимости от всех условий в совокупности определяют общую дисперсию, которая зависит от этих условий:



где - общее среднее для всей изучаемой совокупности, т.е. среднее для всех групп, входящих в совокупность.

Межгрупповая дисперсия отражает вариацию признака изучаемой совокупности, изменение признака которой возникает под влиянием фактора, положенного в основу группировки.

Межгрупповая дисперсия характеризует колеблимость групповых средних около общей средней:



где - средняя величина признака по относительным группам;

- частота отдельных групп.

Средняя внутригрупповая дисперсия характеризует случайную вариацию в каждой отдельной группе. Данная вариация возникает в зависимости от влияния других факторов, которые не учитываются при группировке.



Между общей дисперсией и средней из групповой дисперсии и межгрупповой существует взаимосвязь:

– закон сложения дисперсии
7. Свойства дисперсии.

1. 
   Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:
   

2. 
   Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:
   

3. 
   Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической: , но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:
   

---

используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т.е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:



- ср. квадрат значений признака;

- квадрат среднего значения признака.

Значит, средний квадрат отклонений равен разности между средним квадратом значения признака и квадратом ср. значения признака.


Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы.

Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:



гдеi – величина интервала для данной совокупности ;

Пример.

Рассчитать все показатели вариации, доказать закон сложения дисперсии.

Общий объем ТП	Число предприятий			Расчет общей дисперсии
	Государст- венных	АО	Всего
10-12		3	3	11	33	-7,14	50,9796	152,9388
12-14		4	4	13	52	-5,14	26,4196	105,6784
14-16		17	17	15	255	-3,14	9,8596	167,6132
16-18	11	15	26	17	442	-1,14	1,2996	33,7896
18-20	13	6	19	19	361	0,86	0,7396	14,0524
20-22	18	5	23	21	483	2,86	8,1796	188,1308
22-24	6		6	23	138	4,86	23,6196	141,7176
24-26	2		2	25	50	6,86	47,0596	94,1192
Итого:	50	50	100					898,04

---