Файл: Методические указания к выполнению контрольной работы для студентов заочной формы обучения.docx

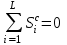), то данные средние и будут окончательными значениями сезонных составляющих (S_i=S^c_i). Если их сумма не равна нулю, то рассчитываются скорректированные значения сезонных составляющих вычитанием из средней оценки величины равной отношению суммы средних оценок к их общему числу ( 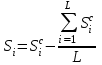). Для нашего примера расчет значений S_i представлен в таблице 8.

Таблица 8

Номер сезона	Год 1	Год 2	Год 3	Средняя оценка сезонной составляющей	Скорректированная оценка сезонной составляяющей Si
1	-	-66,67	-70,00	-68,33	-67,15
2	-1,67	-5,00	-1,67	-2,78	-1,60
3	123,33	180,00	183,33	162,22	163,40
4	-78,33	-113,33	-	-95,83	-94,66
Итого				-4,72	0

---

3) Устранение влияния сезонной составляющей из исходного ряда динамики : x^S= x-S_i. Результаты расчета x^S для нашего примера представлены в столбце 6 таблицы 9.

4) Аналитическое выравнивание уровней x^S (построение тренда): .

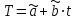Расчет параметров при аналитическом выравнивании чаще всего производится с помощью метода наименьших квадратов (МНК). При этом поиск параметров для линейного уравнения тренда можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю. Для этого вводится новая условная переменная времени t^y, такая, что t^y =0. Уравнение тренда при этом будет следующим: .

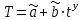При нечетном числе уровней ряда динамики для получения  t^y=0 уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (периоду или моменту времени, соответствующему данному уровню присваивается нулевое значение). Даты времени, расположенные левее этого уровня, обозначаются натуральными числами со знаком минус (-1 –2 –3 ...), а даты времени, расположенные правее этого уровня – натуральными числами со знаком плюс (1 2 3 ...).

Если число уровней ряда четное, периоды времени левой половины ряда (до середины) нумеруются –1, -3, -5 и т.д. А периоды правой половины - +1, +3, +5 и.т.д. При этом t^y будет равна 0.

Система нормальных уравнений (соответствующих МНК) преобразуется к виду:



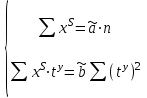
Отсюда параметры уравнения рассчитываются по формулам:

.

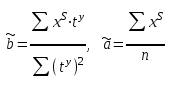Интерпретация параметров линейного уравнения тренда :

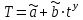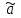- уровень ряда за период времени t^у=0;

- средний абсолютный прирост уровня ряда за единичный промежуток времени.

В нашем примере четное число уровней ряда: n=12. Следовательно, условная переменная времени для 6-ого элемента ряда будет равна –1, а для 7-ого +1. Значения переменной

---

_i^y содержатся во 2-ом столбце таблицы 9.

Параметры линейного тренда будут: =14257,5/572=24,93; =8845/12=737,08. Это значит, что с каждым кварталом объем выпуска товара в среднем увеличивается на 2∙28,7 усл.ед. А средний за период с 1993 по 1995гг объем выпуска составил 738,75 усл.ед.

Рассчитаем значения трендовой компоненты по формуле 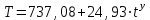(столбец 7 таблицы 9).

5) Учет сезонной составляющей в выровненных уровнях ряда ( =T+S). Результаты расчета для нашего примера представлены в столбце 8 таблицы 9.

6) Расчет абсолютной ошибки временного ряда (Е=x- ) осуществляется для оценки качества полученной модели. Результаты расчета для нашего примера представлены в столбце 9 таблицы 9.
Таблица 9

T	tу	x	xc	x- xc	xs		T		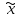	E
1	2	3	4	5	6		7		8	9
1	-11	410	-	-		477,15		462,90	395,75		14,25
2	-9	560	561,67	-1,67		561,60		512,75	511,15		48,85
3	-7	715	591,67	123,33		551,60		562,60	726,00		-11,01
4	-5	500	578,33	-78,33		594,65		612,45	517,80		-17,80
5	-3	520	586,67	-66,67		587,15		662,31	595,15		-75,15
6	-1	740	745,00	-5,00		741,60		712,16	710,56		29,44
7	1	975	795,00	180,00		811,60		762,00	925,41		49,59
8	3	670	783,33	-113,33		764,65		811,86	717,21		-47,21
9	5	705	775,00	-70,00		772,15		861,71	794,56		-89,56
10	7	950	951,67	-1,67		951,60		911,56	909,97		40,03
11	9	1200	1016,67	183,33		1036,60		961,41	1124,82		75,18
12	11	900	-	-		994,65		1011,27	916,61		-16,61
Итого		8845				8845,00		8845,00	8845,00		16,61

1   2   3   4   5   6   7   8

---

Значимость параметров линейного уравнения тренда (Т) определяется на основе t-критерия Стьюдента также как и в линейном парном регрессионном анализе.

Прогнозирование по аддитивной модели.

Пусть требуется дать прогноз уровня временного ряда на период (n+1). Точечный прогноз значения уровня временного ряда х_n+1 в аддитивной модели есть сумма трендовой компоненты и сезонной компоненты (соответствующей i–ому сезону прогноза): 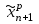=T_n+1+S_i.

Для построения доверительного интервала прогноза нужно рассчитать среднюю ошибку прогноза:

^р = ,

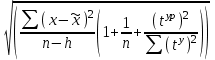где h- число параметров в уравнении тренда;

t^yp – значение условной переменной времени для периода прогнозирования.

Затем рассчитаем предельную ошибку прогноза: ^р =t_a·_р,

где t_a- коэффициент доверия, определяемый по таблицам Стьюдента по уровню значимости α и числу степеней свободы равным (n-h).

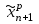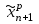Окончательно получим: ( -^р; +^р).

Задание № 4
На основе данных, приведенных в таблице 10 и соответствующих Вашему варианту (таблица 11), постройте модель временного ряда. Для этого требуется:

1. 
   Построить коррелограмму и определить имеет ли ряд тенденцию и сезонные колебания.
   
2. 
   Провести сглаживание ряда скользящей средней и рассчитать значения сезонной составляющей.
   
3. 
   Построить уравнения тренда и сделать выводы.
   
4. 
   На основе полученной модели сделать прогноз на следующие два квартала с учетом выявленной сезонности.
   

Таблица 10

Основные показатели развития производственной фирмы

за период с 2012 по 2017 гг. (по сопоставимой оценке)

N наблюдения	Год	Квартал	Объем производства продукции, млн.руб.	Среднегодовая стоимость основных производственных фондов, млн.руб.	Среднегодовая численность ППП, чел.,	Дебиторская задолженность, млн.руб.	Среднегодовая стоимость оборотных средств, млн.руб.	Балансовая прибыль, млн. руб.	Чистая прибыль, млн. руб.
А	Б	В	1	2	3	4	5	6	7
1	2012	1	1065	1062	713	25	837	94	36
2		2	851	682	507	27	685	78	27
3		3	531	726	361	34	837	87	22
4		4	922	1153	557	44	1161	75	29
5	2013	1	1095	1213	607	42	1151	84	34
6		2	986	898	598	39	822	63	28
7		3	822	794	368	48	1383	86	30
8		4	1137	1441	646	60	884	82	35
9	2014	1	1301	1600	693	63	1309	78	40
10		2	1038	967	718	40	1028	72	33
11		3	780	1246	363	48	1771	84	33
12		4	1435	1458	639	71	1310	102	40
13	2015	1	1593	1412	708	87	1372	112	36
14		2	1658	891	614	65	1272	92	27
15		3	1363	1061	348	67	1821	99	30
16		4	1737	1287	636	76	1571	113	36
17	2016	1	1719	1635	825	101	1758	95	36
18		2	1521	1166	622	84	1505	79	28
19		3	1049	1230	514	73	2109	112	28
20		4	1790	1514	703	93	1787	116	28
21	2017	1	2016	1642	797	96	2197	90	39

---

Таблица 11

Номера наблюдений и показатель,

соответствующие варианту контрольной работы

Номер варианта	Номер начального наблюдения	Номер конечного наблюдения	Номер показателя из табл.4	Номер варианта	Номер начального наблюдения	Номер конечного наблюдения	Номер показателя из табл.4
1	2	3	4	5	6	7	8
1	1	12	1	51	1	12	6
2	2	13	1	52	2	13	6
3	3	14	1	53	3	14	6
4	4	15	1	54	4	15	6
5	5	16	1	55	5	16	6
6	6	17	1	56	6	17	6
7	7	18	1	57	7	18	6
8	8	19	1	58	8	19	6
9	9	20	1	59	9	20	6
10	10	21	1	60	10	21	6
11	1	12	2	61	1	12	7
12	2	13	2	62	2	13	7
13	3	14	2	63	3	14	7
14	4	15	2	64	4	15	7
15	5	16	2	65	5	16	7
16	6	17	2	66	6	17	7
17	7	18	2	67	7	18	7
18	8	19	2	68	8	19	7
19	9	20	2	69	9	20	7
20	10	21	2	70	10	21	7
21	1	12	3	71	1	12	1
22	2	13	3	72	2	13	2
23	3	14	3	73	3	14	3
24	4	15	3	74	4	15	4
25	5	16	3	75	5	16	5
26	6	17	3	76	6	17	6
27	7	18	3	77	7	18	7
28	8	19	3	78	8	19	1
29	9	20	3	79	9	20	2
30	10	21	3	80	10	21	3
31	1	12	4	81	1	12	4
32	2	13	4	82	2	13	5
33	3	14	4	83	3	14	6
34	4	15	4	84	4	15	7
35	5	16	4	85	5	16	1
36	6	17	4	86	6	17	2

---