Файл: Отчет по ознакомительной практике обучающийся гр. Фпмц20 Саранская А. А. 05. 02. 2021 г. 02. 06. 2021 г.docx
Добавлен: 18.01.2024
Просмотров: 109
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(приложение Б)
Раздел 4. Анализ образовательного процесса образовательного учреждения
Документация учителя – предметника по математике 11 класса
Рабочая программа по дисциплине
Содержание учебного предмета алгебра:
Глава 1. Степени и корни. Степенные функции (16 ч)
Глава 2. Показательная и логарифмическая функции (24 ч)
Глава 3. Интеграл (11 ч) Глава 4. Элементы математической статистики, комбинаторики и теории вероятности (17ч) Глава 5. Уравнения и неравенства. Системы уравнений и неравенств (22ч)
Повторение и систематизация учебного материала(14ч)
Содержание учебного предмета геометрия:
Метод координат в пространстве (14 ч)
Тела вращения (15 ч)
Объёмы тел (10 ч)
Итоговое повторение (27 ч)
План – конспект урока по алгебре в 11 классе по теме: «Бином Ньютона.»
Цель: - обучающие: познакомить с формулой бинома Ньютона, научить применять формулу бинома Ньютона при возведении в степень двучлена;
- развивающие: способствовать развитию памяти, алгоритмического и логического мышления, внимания;
- воспитательные: продолжить воспитание чувства ответственности, самостоятельности, добросовестности.)
Ход урока:
1.Организационный момент:
Сообщение темы, целей урока, практической значимости рассматриваемой темы.
2. Актуализация знаний
I. Фронтальный опрос:
1)Что изучает комбинаторика?
2)Какие виды соединений или выборок вам известны?
3) Отгадать кроссворд «Комбинаторика»
II. Устный счет:
5!=….(120), А52 =…(20)., С42=….(8)
Сколькими способами можно разместить 5 человек на скамейке?
3. Изложение нового материала: Работа с карточками теоретического материала. Заслушивание и анализ сообщений студентов. Написание конспекта.
I) История комбинаторики
На прошлом уроке мы познакомились с основами комбинаторики. Домашнее задание для первой творческой группы было подготовить сообщение об истории возникновения комбинаторики как науки.
Какие же ученые внесли вклад в развитие комбинаторики как науки?
Одним из выдающихся умов того времени был английский ученый Исаак Ньютон. Ваше домашнее задание было подготовить сообщение об этом великом гении.
II) Исаак Ньютон- великий математик)
Вы услышали из доклада, сколько гениальных идей и открытий принадлежит великому математику Исааку Ньютону. Одним из его открытий является формула Бином Ньютона.
III) Бином Ньютона.
Именно этому открытию мы посвятим наш сегодняшний урок. Запишем тему урока. Цели нашего урока: познакомиться с формулой бинома Ньютона, научиться применять формулу бинома Ньютона при возведении в степень двучлена.
Слово бином означает «Два числа» В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
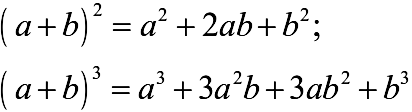
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
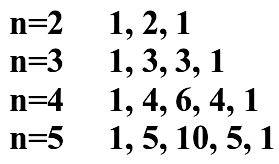
Возможно, вы уже догадались, что «рояль в кустах» – это треугольник Паскаля на предыдущей странице. Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
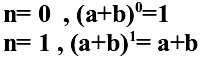
Окончательно получим:
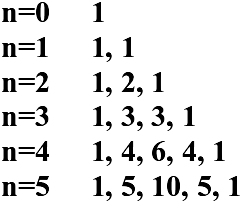
Это утверждение было известно задолго до Паскаля - его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел hello_html_m3478533f.gif (биномиальных коэффициентов) до hello_html_m3fa7df91.gif включительно.
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г. Ваше домашнее задание было подготовить сообщение о французском ученом Паскале.
IV) Блез Паскаль
Теперь понятно, как возвести бином в любую степень n. В левой части записываем (а+b)n. А в правой части записываем сумму аn + аn-1b + … + bn , оставляя в каждом слагаемом место для коэффициента. И эти места заполняем числами из n–ой строчки треугольника Паскаля, которую, конечно, нужно заранее выписать.
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
(a + b)n = an + C1n an - 1 b + C2n an - 2 b2 +...+Ckn an - k bk +... + Cn - 1n abn - 1 + Cnnbn
где Ckn —все возможные сочетания, которые можно образовать из n элементов по k.
Пример:
(a + b)5 = a5 + C15 a4b + C25 a3b2 + C35 a2b3 + C45 ab4 + C55 b5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Таким образом можно записать формулу для возведения двучлена в любую степень. Давайте заметим некоторые свойства у слагаемых в разложении двучлена по формуле Бинома Ньютона.
V) Свойства бинома Ньютона
Число слагаемых на 1 больше степени бинома.
Коэффициенты находятся по треугольнику Паскаля или равны числу сочетаний С, где n – степень двучлена , m – переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
Коэффициенты симметричны.
Если в скобке знак минус, то знаки + и – чередуются.
Сумма степеней каждого слагаемого равна степени бинома.
Сумма коэффициентов разложения ( a + b) n равна 2 n .
Обучающая самостоятельная работа с последующей проверкой
1. Представьте степень двучлена в виде многочлена, используя бином Ньютона
а) (х+у)6
б) (1- 2а)4
Решение:
1а) (х+у)6= х6 +6х5у +15х4 у2 +20х3у3 +15х2у4 +6ху5 +у6.
1б) (1- 2а)4 = 1 * 14 (2а)0 – 4* 13 2а + 6*12 (2а)2 - 4 * 11 * (2а)3 + 1 * 10(2а)4 == 1 - 8а + 24а2 - 32а3 + 16а4.
2. Подведение итогов самостоятельной работы.
VI) Закрепление нового материала.
1) Повторим формулы сокращенного умножения, которые мы с вами знаем.
У доски учащиеся записывают формулы квадрата суммы и разности, формулы куба суммы и куба разности двух выражений.
(а + в)2 = а2+ 2ав + в2
(а – в)2 = а2 – 2ав + в2
(а + в)3= а3 + 3а2в + 3ав2 + в3
(а – в)3= а3 – 3а2в + 3ав2 – в3
2) Попробуйте записать формулу для 4-ой степени
(а+в)4=(а+в)3(а+в)=(а3+3а2в+3ав2+в3)(а+в)= а4 + 3а3в + 3а2в2 + ав3 + а3в + 3а2в2 + 3ав3 + в4 =
= а4 + 4а3в + 6а2в2 + 4ав3 + в4 .
и для 5-ой степени:
(а + в)5= (а + в)4(а + в) = (а4 + 4а3в + 6а2в2 + 4ав3 + в4)(а + в) =
а5 + 4а4в + 6а3в2 + 4а2в3 + в4а + а4в + 4а3в2 + 6а2в3 + 4ав4 + в5 = а5 + 5а4в + 10а3в2 + 10а2в3 + 5ав4 + в5
Внимательно рассмотрим полученные формулы:
n = 0 (а +в)0 = 1
n = 1 (а +в )1 = 1·а+1·в
n = 2 (а + в)2 = 1· а2+ 2·ав +1· в2
n = 3 ( а + в)3 = 1· а3 + 3·а2в + 3·ав2+1· в3
n = 4 ( а + в)4 = 1·а4 + 4·а3в + 6·а2в2+4·а в3 +1·в4
n = 5 (а + в)5 = 1·а5+ 5·а4в+ 10·а3в2+ 10·а2в3+ 5·ав4+ 1·в5
3) Заметим следующее (обсуждаем вместе с учащимися увиденные закономерности):
1. число членов получаемого многочлена на единицу больше показателя степени бинома;
2. показатель степени первого слагаемого убывает от n до 0, показатель степени второго слагаемого возрастает от 0 до n;
3. степени всех одночленов равны степени двучлена в условии;
4. каждый одночлен является произведением первого и второго выражения в различных степенях и некоторого числа; числа– биноминальные коэффициенты;
5. биноминальные коэффициенты, равноотстоящие от начала и конца разложения, равны.
Слово “бином” означает всего-навсего двучлен, т.е. сумму двух слагаемых. Происходит оно от латинских корней: два и слово.
Домашнее задание. Подготовка к контрольной работе.
(задание на листочках каждому ученику)
1. Из 12 членов команды нужно выбрать капитана и заместителя. Сколькими способами можно это сделать?
2.Вычислите: 4Р3+3А210-С25
Выпускники экономического института работают в трех различных организациях: 17 человек в банке,23- в фирме и 19-в налоговой инспекции. Найдите вероятность того, что случайно встреченный выпускник работает в банке?
Имеется 8 различных книг 2 из которых сборники стихов. Сколькими способами можно расставить эти книги на полке так, чтобы справочники оказались рядом?
Для игры в КВН нужно выбрать команду из 6 человек, Сколькими способами можно это сделать, если в команде должно быть мальчиков и девочек поровну, и в классе 12 девочек и 10 мальчиков?
Сколько трехзначных чисел с разными цифрами можно составить из цифр , 0,1,3,6,7,9?
Разложите на множители: (a-b)9 и (3x+y)10
Анализ урока математики в 11 классе по теме: «Бином Ньютона»
По программе на изучение темы: «Бином Ньютона».
Класс организован, дисциплинирован.
Методы: проблемно-диалогический, объяснительно - иллюстративный, частично-поисковый.\
Оборудование: школьная доска, тетради для лекций у учащихся, компьютер, интерактивная доска.
В результате изучения студент должен:
иметь представление о:
биноминальной формуле Ньютона;
принципе построения треугольника Паскаля;
знать:
основные приемы разложения на биноминальные коэффициенты;
уметь:
применять формулу бинома для решения практических заданий;
возводить в любую степень двучлен.
Содержание урока
Соответствует учебной программе по ФГОС, поставленным задачам, способствовало формированию умения сложения дробей с одинаковыми знаменателями. Содержание урока способствовало развитию аналитического мышления.
Тип и структура урока:
Тип урока: урок открытия новых знаний ( и диагностики знаний, умений
навыков)
Для достижения целей весь материал был разделен на три блока:
Что знаем? Что хотим знать? Что узнали?
Знания подлежат прочному усвоению, их объем заложен в программе и они должны быть усвоены каждым учеником. Материал, близко примыкающий к основному, который расширяет и углубляет его и одновременно закладывает основу для дальнейшего изучения тем, рационализации решения текстовых задач.
Целостность знаний способствует общему развитию ученика.
В соответствии с поставленными целями и содержанием материала урок строился по следующим этапам:
Самоопределение к деятельности(орг.момент).(1-2 мин.)
Актуализация знаний и фиксация затруднений в пробном действии(4-5мин.)
Постановка учебной задачи(4-5мин.). Побуждающий от проблемной ситуации диалог.
«Открытие нового знания» (7-8 мин.).
Физическая пауза(1-2 мин.).
Первичное закрепление(4-5мин.).
Самостоятельная работа самопроверкой по эталону (4-5мин).
Включение нового знания в систему знаний и повторение(7-8мин.).
Рефлексия деятельности (2-3мин.).( домашнее задание).
Все структурные элементы урока были выдержаны.
Целью первого этапа было быстро включить учащихся в деловой ритм, проверить готовность класса и оборудование к уроку;
На третьем этапе были актуализированы знания, необходимые для работы над новым материалом. Одновременно шла эффективная работа над развитием речи, мыслительных операций, о чем свидетельствовала деятельность учащихся.
На четвертом этапе для создания проблемной ситуации было использовано уже знакомое задание. Само задание не вызвало затруднения в нахождении результата, таким образом проблемная ситуация мотивировала поиск рационального решения.