ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 706
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
a 10 см. Определите потенциальную энергию П системы этих зарядов.
Задача 326. Точечный электрический заряд q 1 нКл переместился в направлении перпендикулярном тонкой бесконечно длинной равномерно заряженной нити с расстояния r1 2 см до расстояния r2 5 см; при этом силами электрического поля по перемещению заряда была совершена работа A 50 мкДж. Определите линейную плотность электрического заряда, распределенного на нити.
Задача 327. Электростатическое поле создается шаром радиусом R 8 см, равномерно заряженным с объемной плотностью 10 нКл/м3. Определите разность потенциалов (1 2) между двумя точками этого поля, лежащими от центра шара на расстояниях r1 10 см и r2 15 см.
Задача 328. Тонкий стержень, равномерно заряженный с линейной плотностью
133 нКл/м, согнут в полукольцо. Какую работу А нужно совершить силам электростатического поля, чтобы перенести точечный электрический заряд q 6,7 нКл из центра полукольца в бесконечность?
Задача 329. Четыре тонких прямых стержня, равномерно заряженные с линейной плотностью 1,33 нКл/м, образуют квадрат. Определите потенциал электрического поля в центре квадрата.
Задача 330. Протон, начальная скорость движения которого v 100 км/с, влетает
в однородное электрическое поле напряженностью Е 300 В/см так, что вектор скорости совпадает с направлением линий напряженности поля. Какой путь l должен пройти протон в направлении линий поля, чтобы его скорость движения увеличилась в n 2 раза?
Задача 331. В плоский воздушный конденсатор вдвинули плитку парафина толщиной h 1 см, которая вплотную прилегает к его пластинам. На какую величину d нужно увеличить расстояние между пластинами конденсатора, чтобы получить прежнюю электроемкость?
Задача 332. Уединенная металлическая сфера электроемкостью С 10 пФ заряжена
до потенциала 3 кВ. Определите энергию W электрического поля, заключенную в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в n 3 раза больше радиуса сферы.
Задача 333. Конденсатор электроемкостью С1 0,2 мкФ был заряжен до разности
потенциалов U1 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U2 450 В, напряжение на нем увеличилось до величины
U 400 В. Вычислите электроемкость С2 второго конденсатора.
Задача 334. Плоский конденсатор, между пластинами которого находится фарфор, имеет электроемкость С1 111 пФ. Конденсатор зарядили до разности потенциалов U1
600 В и отключили от источника питания. Пренебрегая трением диэлектрика о пластины конденсатора, определите работу А, которую нужно совершить, чтобы вынуть диэлектрик
из конденсатора.
Задача 335. Шар радиусом R1 6 см заряжен до потенциала 1 300 В, а шар радиусом R2 4 см – до потенциала 2 500 В. Шары соединили металлическим проводником. Пренебрегая электроемкостью соединительного проводника, определите потенциал шаров после их соединения.
Задача 336. Конденсатор электроемкостью C1 600 пФ зарядили до разности потенциалов U 1,5 кВ и отключили от источника питания. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С2 400 пФ. Определите энергию W, израсходованную на образование искры, проскочившей при соединении конденсаторов.
Задача 337. Плоский конденсатор, между пластинами которого находится плотно прилегающая стеклянная пластинка, заряжен до разности потенциалов U1 100 В. Какова будет разность потенциалов U2, если вынуть стеклянную пластинку из конденсатора?
Задача 338. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r 10 см каждая. Расстояние между пластинами d1 1 см. Конденсатор зарядили до разности потенциалов U 1,2 кВ и отключили от источника питания. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d2 3,5 см?
Задача 339. Конденсатор электроемкостью C1 0,6 мкФ был заряжен до разности
потенциалов U1 300 В и соединен со вторым конденсатором электроемкостью С2
0,4 мкФ, заряженным до разности потенциалов U2 150 В. Найдите электрический заряд q, перетекший с пластин первого конденсатора на второй.
Задача 340. Сплошной парафиновый шар радиусом R 10 см равномерно заряжен
с объемной плотностью 10 нКл/м3. Определите энергию W электрического поля, сосредоточенную в самом шаре.
Задача 341. При силе тока I1 1 А во внешней цепи батареи аккумуляторов выделяется мощность Р1 10 Вт, а при силе тока
I2 3 А – соответственно мощность Р2 18 Вт. Определите внутреннее сопротивление r и ЭДС E батареи.
Задача 342. Сила тока в проводнике сопротивлением R 3 Ом равномерно увеличивается. За время t 8 с в проводнике выделилось количество теплоты Q 200 Дж. Определите электрический заряд q, прошедший за это время по проводнику, если известно, что в момент времени, принятый за начальный (t 0 с), сила тока в проводнике I 0 А.
Задача 343. К источнику тока с ЭДС E 1,5 В присоединили катушку с сопротивлением R 0,1 Ом; при этом амперметр показал силу тока I1 0,5 А. Когда же к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока в той же катушке оказалась I2 0,4 А. Определите внутренние сопротивления r1 и r2 соответственно первого и второго источников тока.
Задача 344. Сила тока в проводнике сопротивлением R 12 Ом равномерно уменьшается от I 5 А до I 0 А в течение времени t 10 с. Определите количество теплоты Q,выделившейся в этом проводнике за указанный промежуток времени.
Задача 345. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС батареи E 24 В, ее внутреннее сопротивление r 1 Ом. Нагреватель, включенный в электрическую цепь, потребляет мощность P 80 Вт. Вычислите силу тока I в цепи и КПД нагревателя.
Задача 346. Сила тока в проводнике сопротивлением R 3 Ом равномерно увеличивается от I 0 А до некоторого максимального значения в течение времени t 10 с.
За это время в проводнике выделилось количество теплоты Q 1 кДж. Определите скорость нарастания I/t силы тока в проводнике.
Задача 347. В электрическую сеть с напряжением U 100 В подключили катушку
с сопротивлением R1 2 кОм и вольтметр, соединенные последовательно; при этом вольтметр показал напряжение U1 80 В. Когда катушку заменили другой, вольтметр показал напряжение U2 60 В. Определите сопротивление R2 другой катушки.
Задача 348. Сила тока в проводнике изменяется со временем согласно уравнению
I I sin t, где амплитуда силы тока I 10 А, циклическая частота 50 с1. Найдите электрический заряд q, прошедший через поперечное сечение проводника за время t T/2, где T период колебания силы тока в проводнике.
Задача 349. При внешнем сопротивлении R1 50 Ом сила тока в электрической цепи
I1 0,2 А, а при внешнем сопротивлении R2 110 Oм сила тока в цепи I2 0,1 А. Определите силу тока Iкз короткого замыкания источника ЭДС.
Задача 350. При выключении источника тока сила тока в электрической цепи уменьшается со временем согласно уравнению I I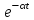 , где начальная сила тока I 10 А, коэффициент 500 с1, e основание натуральных логарифмов. Определите количество теплоты Q, которая выделится в резисторе сопротивлением R 5 Ом после выключения источника тока.
, где начальная сила тока I 10 А, коэффициент 500 с1, e основание натуральных логарифмов. Определите количество теплоты Q, которая выделится в резисторе сопротивлением R 5 Ом после выключения источника тока.
Задача 351. Две батареи аккумуляторов с ЭДС E1 E2 100 В и четыре резистора
с сопротивлениями R1 20 Ом, R2 10 Ом, R3 40 Ом и R4 30 Ом соединены, как показано на рис. 4. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, найдите силу тока IA, которую показывает амперметр.
Задача 352. Три источника тока с ЭДС E1 11 В, E2 4 В и E3 6 В и три реостата
с сопротивлениями R1 5 Ом, R2 10 Ом и R3 2 Ом соединены, как показано на рисунке 5. Пренебрегая внутренними сопротивлениями источников тока, определите силу токов Ii, текущих в каждом реостате.
Задача 353. Две батареи аккумуляторов с одинаковыми ЭДС, два резистора с одинаковыми сопротивлениями R1 R2 100 Ом и вольтметр с сопротивлением RV 150 Ом соединены, как показано на рисунке 6. Пренебрегая внутренними сопротивлениями батареи аккумуляторов, найдите их ЭДС E1 и E2, если вольтметр показывает напряжение U 150 В.
Задача 354. Две батареи аккумуляторов с ЭДС E1 130 В и E2 117 В и три резистора с сопротивлениями R1 1 Ом, R2 0,6 Ом и R3 24 Ом соединены, как показано на рисунке 7. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, определите токи Ii, текущие в отдельных ветвях электрической цепи.
Задача 355. Три резистора с сопротивлениями R1 5 Ом, R2 1 Ом, R3 3 Ом и источник тока с ЭДС E1 1,4 В соединены как показано на рисунке 8. Пренебрегая внутренними сопротивлениями источников тока, определите ЭДС E2 источника тока, который надо подключить в электрическую цепь между точками A и B, чтобы через резистор с сопротивлением R3 протекал ток I3 1 А в направлении, указанном стрелкой.
Задача 356. Два гальванических элемента имеют ЭДС E
Задача 326. Точечный электрический заряд q 1 нКл переместился в направлении перпендикулярном тонкой бесконечно длинной равномерно заряженной нити с расстояния r1 2 см до расстояния r2 5 см; при этом силами электрического поля по перемещению заряда была совершена работа A 50 мкДж. Определите линейную плотность электрического заряда, распределенного на нити.
Задача 327. Электростатическое поле создается шаром радиусом R 8 см, равномерно заряженным с объемной плотностью 10 нКл/м3. Определите разность потенциалов (1 2) между двумя точками этого поля, лежащими от центра шара на расстояниях r1 10 см и r2 15 см.
Задача 328. Тонкий стержень, равномерно заряженный с линейной плотностью
133 нКл/м, согнут в полукольцо. Какую работу А нужно совершить силам электростатического поля, чтобы перенести точечный электрический заряд q 6,7 нКл из центра полукольца в бесконечность?
Задача 329. Четыре тонких прямых стержня, равномерно заряженные с линейной плотностью 1,33 нКл/м, образуют квадрат. Определите потенциал электрического поля в центре квадрата.
Задача 330. Протон, начальная скорость движения которого v 100 км/с, влетает
в однородное электрическое поле напряженностью Е 300 В/см так, что вектор скорости совпадает с направлением линий напряженности поля. Какой путь l должен пройти протон в направлении линий поля, чтобы его скорость движения увеличилась в n 2 раза?
Задача 331. В плоский воздушный конденсатор вдвинули плитку парафина толщиной h 1 см, которая вплотную прилегает к его пластинам. На какую величину d нужно увеличить расстояние между пластинами конденсатора, чтобы получить прежнюю электроемкость?
Задача 332. Уединенная металлическая сфера электроемкостью С 10 пФ заряжена
до потенциала 3 кВ. Определите энергию W электрического поля, заключенную в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в n 3 раза больше радиуса сферы.
Задача 333. Конденсатор электроемкостью С1 0,2 мкФ был заряжен до разности
потенциалов U1 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U2 450 В, напряжение на нем увеличилось до величины
U 400 В. Вычислите электроемкость С2 второго конденсатора.
Задача 334. Плоский конденсатор, между пластинами которого находится фарфор, имеет электроемкость С1 111 пФ. Конденсатор зарядили до разности потенциалов U1
600 В и отключили от источника питания. Пренебрегая трением диэлектрика о пластины конденсатора, определите работу А, которую нужно совершить, чтобы вынуть диэлектрик
из конденсатора.
Задача 335. Шар радиусом R1 6 см заряжен до потенциала 1 300 В, а шар радиусом R2 4 см – до потенциала 2 500 В. Шары соединили металлическим проводником. Пренебрегая электроемкостью соединительного проводника, определите потенциал шаров после их соединения.
Задача 336. Конденсатор электроемкостью C1 600 пФ зарядили до разности потенциалов U 1,5 кВ и отключили от источника питания. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С2 400 пФ. Определите энергию W, израсходованную на образование искры, проскочившей при соединении конденсаторов.
Задача 337. Плоский конденсатор, между пластинами которого находится плотно прилегающая стеклянная пластинка, заряжен до разности потенциалов U1 100 В. Какова будет разность потенциалов U2, если вынуть стеклянную пластинку из конденсатора?
Задача 338. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r 10 см каждая. Расстояние между пластинами d1 1 см. Конденсатор зарядили до разности потенциалов U 1,2 кВ и отключили от источника питания. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d2 3,5 см?
Задача 339. Конденсатор электроемкостью C1 0,6 мкФ был заряжен до разности
потенциалов U1 300 В и соединен со вторым конденсатором электроемкостью С2
0,4 мкФ, заряженным до разности потенциалов U2 150 В. Найдите электрический заряд q, перетекший с пластин первого конденсатора на второй.
Задача 340. Сплошной парафиновый шар радиусом R 10 см равномерно заряжен
с объемной плотностью 10 нКл/м3. Определите энергию W электрического поля, сосредоточенную в самом шаре.
Задача 341. При силе тока I1 1 А во внешней цепи батареи аккумуляторов выделяется мощность Р1 10 Вт, а при силе тока
I2 3 А – соответственно мощность Р2 18 Вт. Определите внутреннее сопротивление r и ЭДС E батареи.
Задача 342. Сила тока в проводнике сопротивлением R 3 Ом равномерно увеличивается. За время t 8 с в проводнике выделилось количество теплоты Q 200 Дж. Определите электрический заряд q, прошедший за это время по проводнику, если известно, что в момент времени, принятый за начальный (t 0 с), сила тока в проводнике I 0 А.
Задача 343. К источнику тока с ЭДС E 1,5 В присоединили катушку с сопротивлением R 0,1 Ом; при этом амперметр показал силу тока I1 0,5 А. Когда же к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока в той же катушке оказалась I2 0,4 А. Определите внутренние сопротивления r1 и r2 соответственно первого и второго источников тока.
Задача 344. Сила тока в проводнике сопротивлением R 12 Ом равномерно уменьшается от I 5 А до I 0 А в течение времени t 10 с. Определите количество теплоты Q,выделившейся в этом проводнике за указанный промежуток времени.
Задача 345. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС батареи E 24 В, ее внутреннее сопротивление r 1 Ом. Нагреватель, включенный в электрическую цепь, потребляет мощность P 80 Вт. Вычислите силу тока I в цепи и КПД нагревателя.
Задача 346. Сила тока в проводнике сопротивлением R 3 Ом равномерно увеличивается от I 0 А до некоторого максимального значения в течение времени t 10 с.
За это время в проводнике выделилось количество теплоты Q 1 кДж. Определите скорость нарастания I/t силы тока в проводнике.
Задача 347. В электрическую сеть с напряжением U 100 В подключили катушку
с сопротивлением R1 2 кОм и вольтметр, соединенные последовательно; при этом вольтметр показал напряжение U1 80 В. Когда катушку заменили другой, вольтметр показал напряжение U2 60 В. Определите сопротивление R2 другой катушки.
Задача 348. Сила тока в проводнике изменяется со временем согласно уравнению
I I sin t, где амплитуда силы тока I 10 А, циклическая частота 50 с1. Найдите электрический заряд q, прошедший через поперечное сечение проводника за время t T/2, где T период колебания силы тока в проводнике.
Задача 349. При внешнем сопротивлении R1 50 Ом сила тока в электрической цепи
I1 0,2 А, а при внешнем сопротивлении R2 110 Oм сила тока в цепи I2 0,1 А. Определите силу тока Iкз короткого замыкания источника ЭДС.
Задача 350. При выключении источника тока сила тока в электрической цепи уменьшается со временем согласно уравнению I I
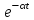 , где начальная сила тока I 10 А, коэффициент 500 с1, e основание натуральных логарифмов. Определите количество теплоты Q, которая выделится в резисторе сопротивлением R 5 Ом после выключения источника тока.
, где начальная сила тока I 10 А, коэффициент 500 с1, e основание натуральных логарифмов. Определите количество теплоты Q, которая выделится в резисторе сопротивлением R 5 Ом после выключения источника тока.Задача 351. Две батареи аккумуляторов с ЭДС E1 E2 100 В и четыре резистора
с сопротивлениями R1 20 Ом, R2 10 Ом, R3 40 Ом и R4 30 Ом соединены, как показано на рис. 4. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, найдите силу тока IA, которую показывает амперметр.
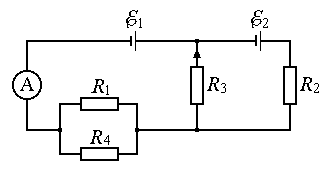 | 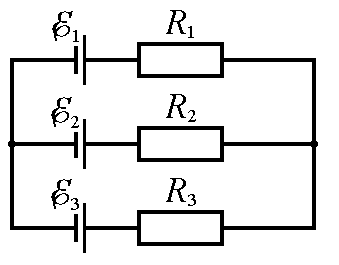 |
| Рис. 4 | Рис. 5 |
Задача 352. Три источника тока с ЭДС E1 11 В, E2 4 В и E3 6 В и три реостата
с сопротивлениями R1 5 Ом, R2 10 Ом и R3 2 Ом соединены, как показано на рисунке 5. Пренебрегая внутренними сопротивлениями источников тока, определите силу токов Ii, текущих в каждом реостате.
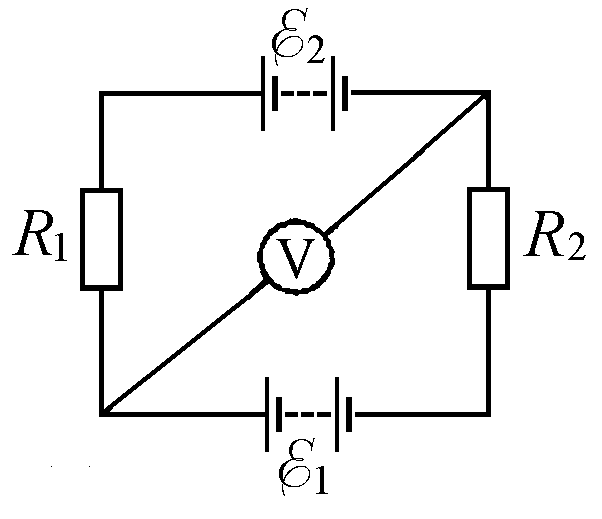
Задача 353. Две батареи аккумуляторов с одинаковыми ЭДС, два резистора с одинаковыми сопротивлениями R1 R2 100 Ом и вольтметр с сопротивлением RV 150 Ом соединены, как показано на рисунке 6. Пренебрегая внутренними сопротивлениями батареи аккумуляторов, найдите их ЭДС E1 и E2, если вольтметр показывает напряжение U 150 В.
 |  |
| Рис. 6 | Рис. 7 |
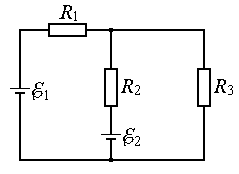
Задача 354. Две батареи аккумуляторов с ЭДС E1 130 В и E2 117 В и три резистора с сопротивлениями R1 1 Ом, R2 0,6 Ом и R3 24 Ом соединены, как показано на рисунке 7. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, определите токи Ii, текущие в отдельных ветвях электрической цепи.
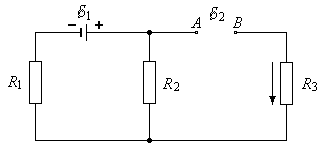
Задача 355. Три резистора с сопротивлениями R1 5 Ом, R2 1 Ом, R3 3 Ом и источник тока с ЭДС E1 1,4 В соединены как показано на рисунке 8. Пренебрегая внутренними сопротивлениями источников тока, определите ЭДС E2 источника тока, который надо подключить в электрическую цепь между точками A и B, чтобы через резистор с сопротивлением R3 протекал ток I3 1 А в направлении, указанном стрелкой.
 |  |
| Рис. 8 | Рис. 9 |
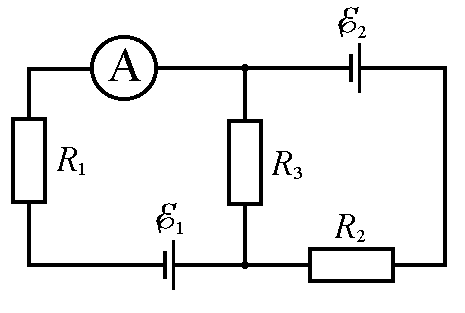
Задача 356. Два гальванических элемента имеют ЭДС E