Добавлен: 04.02.2024
Просмотров: 493
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
нужное количество членов с нулевыми коэффициентами). Тогда суммой многочленов  и
и  называется многочлен
называется многочлен
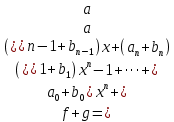
Произведением многочленов и
и  , определенных согласно (1.2) и (1.3) (при любых соотношениях между
, определенных согласно (1.2) и (1.3) (при любых соотношениях между 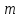 и
и  ), называется
), называется

т.е
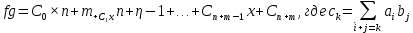 (1.4)
(1.4)
Из определения суммы многочленов получаем:
Утверждение 1.1. Пусть ,
,  — многочлены из
— многочлены из 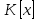 . Тогда
. Тогда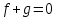 , либо
, либо
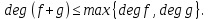
Если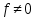 и
и , то
, то
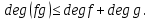
Если при этом K не содержит делителей нуля, то
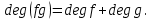 (1.5)
(1.5)
Теорема 1.2. Пусть — некоторое кольцо. Тогда множество многочленов
— некоторое кольцо. Тогда множество многочленов 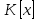 образует кольцо. Это кольцо является ассоциативным, коммутативным, содержит единицу и не содержит делителей нуля тогда и только тогда, когда кольцо
образует кольцо. Это кольцо является ассоциативным, коммутативным, содержит единицу и не содержит делителей нуля тогда и только тогда, когда кольцо  соответственно ассоциативно, коммутативно, содержит единицу и не содержит делителей нуля. В частности, если
соответственно ассоциативно, коммутативно, содержит единицу и не содержит делителей нуля. В частности, если 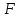 — поле, то
— поле, то 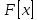
— ассоциативное, коммутативное кольцо с единицей и без делителей нуля.
Доказательство. Операции сложения и умножения обладают следующими легко проверяемыми свойствами: для любых многочленов ,
,  и
и  справедливо
справедливо
1) (коммутативность сложения),
(коммутативность сложения),
2) (ассоциативность сложения),
(ассоциативность сложения),
3)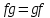 , если
, если  — коммутативное кольцо (коммутативность умножения),
— коммутативное кольцо (коммутативность умножения),
4) , если
, если  — ассоциативное кольцо (ассоциативность умножения),
— ассоциативное кольцо (ассоциативность умножения),
5) (дистрибутивность),
(дистрибутивность),
6)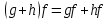 ( (дистрибутивность).
( (дистрибутивность).
Докажем, например, ассоциативность умножения многочленов, если — ассоциативное кольцо. Если
— ассоциативное кольцо. Если  и
и  определены согласно (1.2) и (1.3) соответственно и
определены согласно (1.2) и (1.3) соответственно и
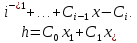
то
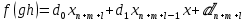
где, согласно (1.4) (мы пользуемся дистрибутивностью в кольце ),
),
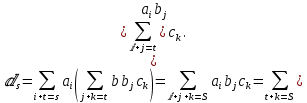
Аналогично, если

откуда .
.
Легко видеть, что в константа 0 (и только она) является нейтральным элементом относительно сложения, т. е. для любого
константа 0 (и только она) является нейтральным элементом относительно сложения, т. е. для любого 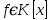 справедливо
справедливо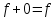 . Для многочлена
. Для многочлена
 противоположным (относительно сложения) является
противоположным (относительно сложения) является
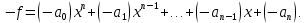
Под операцией вычитания тогда понимается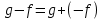 . Если кольцо
. Если кольцо  содержит единицу 1, то
содержит единицу 1, то  также содержит 1. Константа 1 (и только она) является нейтральным элементом относительно умножения в
также содержит 1. Константа 1 (и только она) является нейтральным элементом относительно умножения в  . Из (1.5) получаем, что если в
. Из (1.5) получаем, что если в  нет делителей нуля, то в
нет делителей нуля, то в  также нет делителей нуля, т. е. из равенства
также нет делителей нуля, т. е. из равенства 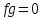 следует, что
следует, что  или
или 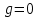 .
.
С многочленами над числовым кольцом можно проводить операции сложения, вычитания и умножения. Данные операции сводятся к приведению подобных членов. Ясно, что в результате получится многочлен с коэффициентами из этого же кольца. Выразим коэффициенты произведения многочленов через коэффициенты сомножителей. Пусть в результате перемножения многочленов получается многочлен
получается многочлен 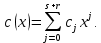 Тогда
Тогда 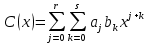 и после
и после  приведения подобных получим
приведения подобных получим 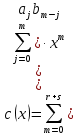 , в правой части равенства предполагается, что
, в правой части равенства предполагается, что 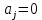 при
при 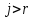 и
и 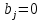 при
при 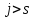
. Таким образом, найдены формулы для вычисления коэффициентов произведения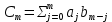 , где
, где 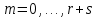 .
.
C многочленами над числовым полем, кроме перечисленных операций, определена операция деления с остатком. Задача деления многочлена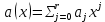 на многочлен
на многочлен 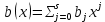 может быть сформулирована следующим образом: найти такой многочлен
может быть сформулирована следующим образом: найти такой многочлен 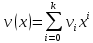 , называемый частным, при котором степень многочлена
, называемый частным, при котором степень многочлена 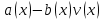 -наименьшая. Многочлен
-наименьшая. Многочлен  называется остатком деления
называется остатком деления  на
на  . Говорят, что многочлен
. Говорят, что многочлен  делится на многочлен
делится на многочлен  , если остаток от деления равен нулю. Если степень
, если остаток от деления равен нулю. Если степень  меньше степени
меньше степени  , то частное равно нулю. Пусть степень
, то частное равно нулю. Пусть степень  не меньше степени
не меньше степени  . Из требования минимальности степени
. Из требования минимальности степени  и правила умножения многочленов выводим, что степень
и правила умножения многочленов выводим, что степень  не превосходит
не превосходит 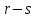 и
и 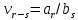 . Задача деления многочлена
. Задача деления многочлена  на многочлен
на многочлен  сводится к аналогичной задаче деления многочлена
сводится к аналогичной задаче деления многочлена 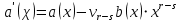 , но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют «уголком» и чисто внешне похож на деление целых чисел с остатком. В качестве примера, деление «уголком» многочлена
, но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют «уголком» и чисто внешне похож на деление целых чисел с остатком. В качестве примера, деление «уголком» многочлена
 на многочлен
на многочлен  с остатком приведено на рисунке ниже.
с остатком приведено на рисунке ниже.

При делении на двучлен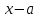 можно воспользоваться более компактной схемой деления, называемой схемой Горнера. В основе этой схемы лежит очевидный факт, что при выполнении деления «уголком» на каждом шаге меняется только один коэффициент в текущем «остатке». Поэтому, схему деления «уголком» можно записать в одну строчку. Для примера, поделим многочлен
можно воспользоваться более компактной схемой деления, называемой схемой Горнера. В основе этой схемы лежит очевидный факт, что при выполнении деления «уголком» на каждом шаге меняется только один коэффициент в текущем «остатке». Поэтому, схему деления «уголком» можно записать в одну строчку. Для примера, поделим многочлен  на двучлен
на двучлен 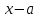 по схеме Горнера. Результат приведен на рисунке ниже.
по схеме Горнера. Результат приведен на рисунке ниже.

Кроме перечисленных операций используется операция подстановки в многочлен, или вычисления значения многочлена в точке. При выполнении данной операции, вместо переменной подставляют число. В результате получается числовое выражение, значение которого и называется значением многочлена. Число, значение многочлена в котором равно 0, называется корнем многочлена. Теорема Безе утверждает, что остаток от деления многочлена на двучлен
на двучлен 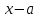 равен
равен  . Таким образом, схему Горнера можно использовать не только для вычисления частного и остатка от деления на двучлен, но и для вычисления значения многочлена в точке. [3]
. Таким образом, схему Горнера можно использовать не только для вычисления частного и остатка от деления на двучлен, но и для вычисления значения многочлена в точке. [3]
 и
и  называется многочлен
называется многочлен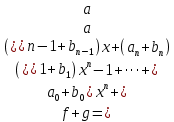
Произведением многочленов
 и
и  , определенных согласно (1.2) и (1.3) (при любых соотношениях между
, определенных согласно (1.2) и (1.3) (при любых соотношениях между 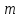 и
и  ), называется
), называется
т.е
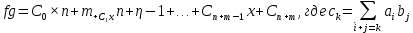 (1.4)
(1.4)Из определения суммы многочленов получаем:
Утверждение 1.1. Пусть
 ,
,  — многочлены из
— многочлены из 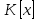 . Тогда
. Тогда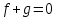 , либо
, либо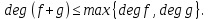
Если
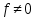 и
и , то
, то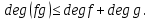
Если при этом K не содержит делителей нуля, то
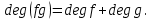 (1.5)
(1.5) Теорема 1.2. Пусть
 — некоторое кольцо. Тогда множество многочленов
— некоторое кольцо. Тогда множество многочленов 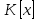 образует кольцо. Это кольцо является ассоциативным, коммутативным, содержит единицу и не содержит делителей нуля тогда и только тогда, когда кольцо
образует кольцо. Это кольцо является ассоциативным, коммутативным, содержит единицу и не содержит делителей нуля тогда и только тогда, когда кольцо  соответственно ассоциативно, коммутативно, содержит единицу и не содержит делителей нуля. В частности, если
соответственно ассоциативно, коммутативно, содержит единицу и не содержит делителей нуля. В частности, если 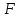 — поле, то
— поле, то 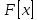
— ассоциативное, коммутативное кольцо с единицей и без делителей нуля.
Доказательство. Операции сложения и умножения обладают следующими легко проверяемыми свойствами: для любых многочленов
 ,
,  и
и  справедливо
справедливо1)
 (коммутативность сложения),
(коммутативность сложения), 2)
 (ассоциативность сложения),
(ассоциативность сложения), 3)
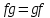 , если
, если  — коммутативное кольцо (коммутативность умножения),
— коммутативное кольцо (коммутативность умножения), 4)
 , если
, если  — ассоциативное кольцо (ассоциативность умножения),
— ассоциативное кольцо (ассоциативность умножения), 5)
 (дистрибутивность),
(дистрибутивность), 6)
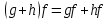 ( (дистрибутивность).
( (дистрибутивность).Докажем, например, ассоциативность умножения многочленов, если
 — ассоциативное кольцо. Если
— ассоциативное кольцо. Если  и
и  определены согласно (1.2) и (1.3) соответственно и
определены согласно (1.2) и (1.3) соответственно и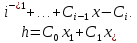
то
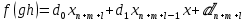
где, согласно (1.4) (мы пользуемся дистрибутивностью в кольце
 ),
),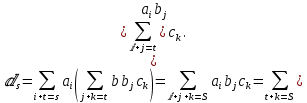
Аналогично, если

откуда
 .
.Легко видеть, что в
 константа 0 (и только она) является нейтральным элементом относительно сложения, т. е. для любого
константа 0 (и только она) является нейтральным элементом относительно сложения, т. е. для любого 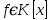 справедливо
справедливо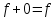 . Для многочлена
. Для многочлена
 противоположным (относительно сложения) является
противоположным (относительно сложения) является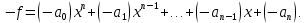
Под операцией вычитания тогда понимается
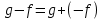 . Если кольцо
. Если кольцо  содержит единицу 1, то
содержит единицу 1, то  также содержит 1. Константа 1 (и только она) является нейтральным элементом относительно умножения в
также содержит 1. Константа 1 (и только она) является нейтральным элементом относительно умножения в  . Из (1.5) получаем, что если в
. Из (1.5) получаем, что если в  нет делителей нуля, то в
нет делителей нуля, то в  также нет делителей нуля, т. е. из равенства
также нет делителей нуля, т. е. из равенства 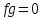 следует, что
следует, что  или
или 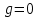 .
.-
Операции над многочленами
С многочленами над числовым кольцом можно проводить операции сложения, вычитания и умножения. Данные операции сводятся к приведению подобных членов. Ясно, что в результате получится многочлен с коэффициентами из этого же кольца. Выразим коэффициенты произведения многочленов через коэффициенты сомножителей. Пусть в результате перемножения многочленов
 получается многочлен
получается многочлен 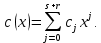 Тогда
Тогда 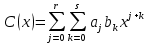 и после
и после  приведения подобных получим
приведения подобных получим 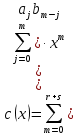 , в правой части равенства предполагается, что
, в правой части равенства предполагается, что 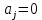 при
при 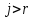 и
и 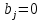 при
при 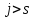
. Таким образом, найдены формулы для вычисления коэффициентов произведения
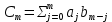 , где
, где 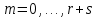 .
.C многочленами над числовым полем, кроме перечисленных операций, определена операция деления с остатком. Задача деления многочлена
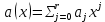 на многочлен
на многочлен 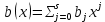 может быть сформулирована следующим образом: найти такой многочлен
может быть сформулирована следующим образом: найти такой многочлен 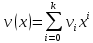 , называемый частным, при котором степень многочлена
, называемый частным, при котором степень многочлена 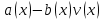 -наименьшая. Многочлен
-наименьшая. Многочлен  называется остатком деления
называется остатком деления  на
на  . Говорят, что многочлен
. Говорят, что многочлен  делится на многочлен
делится на многочлен  , если остаток от деления равен нулю. Если степень
, если остаток от деления равен нулю. Если степень  меньше степени
меньше степени  , то частное равно нулю. Пусть степень
, то частное равно нулю. Пусть степень  не меньше степени
не меньше степени  . Из требования минимальности степени
. Из требования минимальности степени  и правила умножения многочленов выводим, что степень
и правила умножения многочленов выводим, что степень  не превосходит
не превосходит 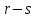 и
и 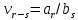 . Задача деления многочлена
. Задача деления многочлена  на многочлен
на многочлен  сводится к аналогичной задаче деления многочлена
сводится к аналогичной задаче деления многочлена 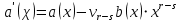 , но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют «уголком» и чисто внешне похож на деление целых чисел с остатком. В качестве примера, деление «уголком» многочлена
, но уже меньшей степени. Понятно, что таким образом частное и остаток от деления определяются единственным образом. Алгоритм деления оформляют «уголком» и чисто внешне похож на деление целых чисел с остатком. В качестве примера, деление «уголком» многочлена
 на многочлен
на многочлен  с остатком приведено на рисунке ниже.
с остатком приведено на рисунке ниже.
При делении на двучлен
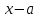 можно воспользоваться более компактной схемой деления, называемой схемой Горнера. В основе этой схемы лежит очевидный факт, что при выполнении деления «уголком» на каждом шаге меняется только один коэффициент в текущем «остатке». Поэтому, схему деления «уголком» можно записать в одну строчку. Для примера, поделим многочлен
можно воспользоваться более компактной схемой деления, называемой схемой Горнера. В основе этой схемы лежит очевидный факт, что при выполнении деления «уголком» на каждом шаге меняется только один коэффициент в текущем «остатке». Поэтому, схему деления «уголком» можно записать в одну строчку. Для примера, поделим многочлен  на двучлен
на двучлен 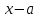 по схеме Горнера. Результат приведен на рисунке ниже.
по схеме Горнера. Результат приведен на рисунке ниже.
Кроме перечисленных операций используется операция подстановки в многочлен, или вычисления значения многочлена в точке. При выполнении данной операции, вместо переменной подставляют число. В результате получается числовое выражение, значение которого и называется значением многочлена. Число, значение многочлена в котором равно 0, называется корнем многочлена. Теорема Безе утверждает, что остаток от деления многочлена
 на двучлен
на двучлен 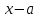 равен
равен  . Таким образом, схему Горнера можно использовать не только для вычисления частного и остатка от деления на двучлен, но и для вычисления значения многочлена в точке. [3]
. Таким образом, схему Горнера можно использовать не только для вычисления частного и остатка от деления на двучлен, но и для вычисления значения многочлена в точке. [3]