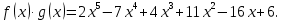Добавлен: 04.02.2024
Просмотров: 497
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
в равенство  , будем иметь:
, будем иметь:
Итак, любое любое общее кратное многочленов и
и  ) делится на
) делится на  ). Следовательно,
). Следовательно,  ) есть НОК многочленов
) есть НОК многочленов  и
и  ). Теорема доказана. [1,2,11]
). Теорема доказана. [1,2,11]
Пример 1. Найти НОК многочленов.

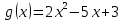
Решение:
А)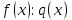 . Получаем, что
. Получаем, что 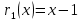 ;
;
Б) . Получаем, что
. Получаем, что  ;
;
Итак, НОД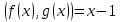 .
.
По схеме Горнера
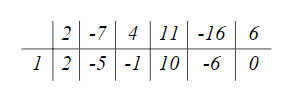
Ответ: .
.
Пусть даны целые числа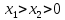 . Для вычисления наибольшего делителя
. Для вычисления наибольшего делителя 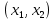 существует хорошо известный алгоритм Евклида.
существует хорошо известный алгоритм Евклида.
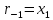
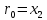
 ,
, 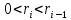 ,
, 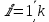
Тогда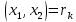 и для его нахождения требуется выполнить
и для его нахождения требуется выполнить 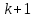 делений с остатком. Оценим сначала количество шагов алгоритма Евклида.[4]
делений с остатком. Оценим сначала количество шагов алгоритма Евклида.[4]
Определение 3. Последовательностью чисел Фибоначчи называется рекуррентная последовательность вида
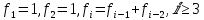
Обозначим также через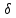 положительный корень квадратного уравнения
положительный корень квадратного уравнения 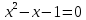
Лемма 1. При любом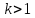 справедливо неравенство
справедливо неравенство 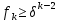 .
.
Доказательство проведем индукцией по . При
. При 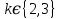 неравенство проверяется непосредственно. Далее, используя предположение индукции и определение последовательности Фибоначчи, имеем
неравенство проверяется непосредственно. Далее, используя предположение индукции и определение последовательности Фибоначчи, имеем
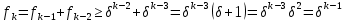
Теорема 1.3. Число делений с остатком в алгоритме Евклида для нахождения наибольшего общего делителя чисел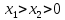 не превосходят величины
не превосходят величины 
Доказательство. Индукцией по докажем, что
докажем, что
 . При
. При 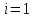 данное неравенство выполнено, так как
данное неравенство выполнено, так как 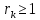 . Для
. Для 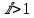 в силу предположения индукции имеем
в силу предположения индукции имеем
 .
.
В силу доказанного или
или 
Из последнего неравенства следует оценка числа шагов алгоритма Евклида. Теперь оценим сложность алгоритма Евклида. Пусть , где
, где  - число шагов алгоритма. Очевидно, выполняются условия
- число шагов алгоритма. Очевидно, выполняются условия
 . Тогда, учитывая сложность деления с остатком, можно оценить сложность алгоритма Евклида величиной
. Тогда, учитывая сложность деления с остатком, можно оценить сложность алгоритма Евклида величиной
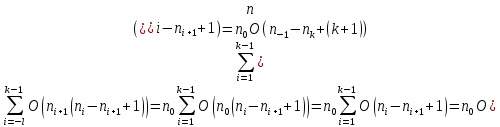 .
.
Так как оценивается теоремой 1.3 как
оценивается теоремой 1.3 как 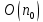 , то сложность всего алгоритма можно оценивать величиной
, то сложность всего алгоритма можно оценивать величиной 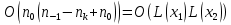 . Если длина чисел
. Если длина чисел 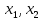 не превосходит
не превосходит  , то полученная оценка имеет вид
, то полученная оценка имеет вид 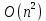 .
.
Без доказательства приведем еще одну оценку для количества шагов алгоритма Евклида. [7]
Теорема 1.4. Число делений с остатком в алгоритме Евклида для нахождения наибольшего общего делителя не превосходит величины
не превосходит величины 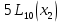 .
.
Замечание. Оценка теоремы Ламе достижима. Так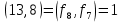 , и для нахождения наибольшего общего делителя требуется ровно 5 шагов алгоритма Евклида.
, и для нахождения наибольшего общего делителя требуется ровно 5 шагов алгоритма Евклида.
Приведем также без доказательства теорему о среднем числе шагов алгоритма Евклида.
Теорема 1.5. Если целочисленные случайные величины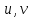 равномерно и независимо распределены на множестве
равномерно и независимо распределены на множестве  , и
, и 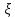 - случайная величина, равная числу шагов алгоритма Евклида нахождения
- случайная величина, равная числу шагов алгоритма Евклида нахождения  , то
, то
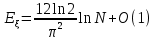 .
.
При переходе к десятичным логарифмам имеем . Значит, полученные выше оценки числа шагов алгоритма Евклида в среднем завышены примерно в два с половиной раза. [4]
. Значит, полученные выше оценки числа шагов алгоритма Евклида в среднем завышены примерно в два с половиной раза. [4]
Пусть алгоритм Евклида на каждом шаге, кроме частного и остатка
и остатка 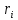 , вычисляет еще два значения
, вычисляет еще два значения  по правилу
по правилу
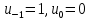
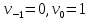
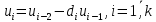
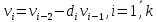
Такой алгоритм будет называться расширенным алгоритмом Евклида. В расширенном алгоритме Евклида для всех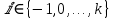 выполняется равенство
выполняется равенство 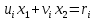 . Значение расширенного алгоритма Евклида состоит в том, что он дает линейное разложение наибольшего общего делителя
. Значение расширенного алгоритма Евклида состоит в том, что он дает линейное разложение наибольшего общего делителя 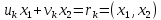 , которое играет важнейшую роль в операциях модульной арифметики.
, которое играет важнейшую роль в операциях модульной арифметики.
Легко показать, что длина чисел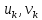 оценивается величиной
оценивается величиной 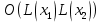 . Значит, сложность расширенного алгоритма Евклида отличается от сложности обычного алгоритма Евклида не более чем на константный множитель, т.е. для расширенного алгоритма Евклида сохраняется оценка сложности
. Значит, сложность расширенного алгоритма Евклида отличается от сложности обычного алгоритма Евклида не более чем на константный множитель, т.е. для расширенного алгоритма Евклида сохраняется оценка сложности 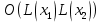 . [6]
. [6]
Рассмотрим сначала один из простейших способов ускорения работы алгоритма Евклида. Пусть в ходе выполнения алгоритма вычисляются величины

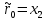
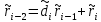 ,
, 
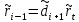
Здесь на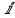
 , будем иметь:
, будем иметь: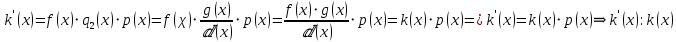
Итак, любое любое общее кратное многочленов
 и
и  ) делится на
) делится на  ). Следовательно,
). Следовательно,  ) есть НОК многочленов
) есть НОК многочленов  и
и  ). Теорема доказана. [1,2,11]
). Теорема доказана. [1,2,11]Пример 1. Найти НОК многочленов.

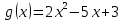
Решение:
-
Найдем НОД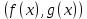
А)
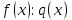 . Получаем, что
. Получаем, что 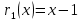 ;
;Б)
 . Получаем, что
. Получаем, что  ;
;Итак, НОД
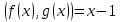 .
.По схеме Горнера

Ответ:
 .
.2.3 Алгоритм Евклида нахождения наибольшего общего делителя двух чисел
Пусть даны целые числа
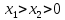 . Для вычисления наибольшего делителя
. Для вычисления наибольшего делителя 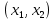 существует хорошо известный алгоритм Евклида.
существует хорошо известный алгоритм Евклида.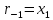
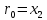
 ,
, 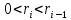 ,
, 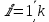
Тогда
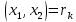 и для его нахождения требуется выполнить
и для его нахождения требуется выполнить 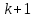 делений с остатком. Оценим сначала количество шагов алгоритма Евклида.[4]
делений с остатком. Оценим сначала количество шагов алгоритма Евклида.[4]Определение 3. Последовательностью чисел Фибоначчи называется рекуррентная последовательность вида
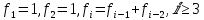
Обозначим также через
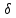 положительный корень квадратного уравнения
положительный корень квадратного уравнения 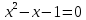
Лемма 1. При любом
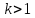 справедливо неравенство
справедливо неравенство 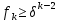 .
.Доказательство проведем индукцией по
 . При
. При 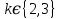 неравенство проверяется непосредственно. Далее, используя предположение индукции и определение последовательности Фибоначчи, имеем
неравенство проверяется непосредственно. Далее, используя предположение индукции и определение последовательности Фибоначчи, имеем 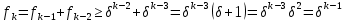
Теорема 1.3. Число делений с остатком в алгоритме Евклида для нахождения наибольшего общего делителя чисел
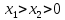 не превосходят величины
не превосходят величины 
Доказательство. Индукцией по
 докажем, что
докажем, что
 . При
. При 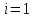 данное неравенство выполнено, так как
данное неравенство выполнено, так как 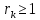 . Для
. Для 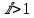 в силу предположения индукции имеем
в силу предположения индукции имеем .
.В силу доказанного
 или
или 
Из последнего неравенства следует оценка числа шагов алгоритма Евклида. Теперь оценим сложность алгоритма Евклида. Пусть
 , где
, где  - число шагов алгоритма. Очевидно, выполняются условия
- число шагов алгоритма. Очевидно, выполняются условия . Тогда, учитывая сложность деления с остатком, можно оценить сложность алгоритма Евклида величиной
. Тогда, учитывая сложность деления с остатком, можно оценить сложность алгоритма Евклида величиной 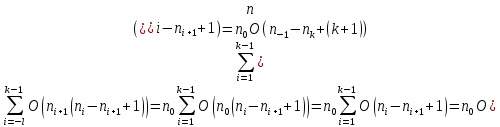 .
.Так как
 оценивается теоремой 1.3 как
оценивается теоремой 1.3 как 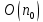 , то сложность всего алгоритма можно оценивать величиной
, то сложность всего алгоритма можно оценивать величиной 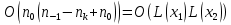 . Если длина чисел
. Если длина чисел 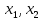 не превосходит
не превосходит  , то полученная оценка имеет вид
, то полученная оценка имеет вид 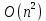 .
.Без доказательства приведем еще одну оценку для количества шагов алгоритма Евклида. [7]
Теорема 1.4. Число делений с остатком в алгоритме Евклида для нахождения наибольшего общего делителя
 не превосходит величины
не превосходит величины 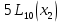 .
.Замечание. Оценка теоремы Ламе достижима. Так
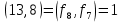 , и для нахождения наибольшего общего делителя требуется ровно 5 шагов алгоритма Евклида.
, и для нахождения наибольшего общего делителя требуется ровно 5 шагов алгоритма Евклида. Приведем также без доказательства теорему о среднем числе шагов алгоритма Евклида.
Теорема 1.5. Если целочисленные случайные величины
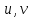 равномерно и независимо распределены на множестве
равномерно и независимо распределены на множестве  , и
, и 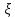 - случайная величина, равная числу шагов алгоритма Евклида нахождения
- случайная величина, равная числу шагов алгоритма Евклида нахождения  , то
, то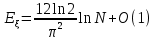 .
.При переходе к десятичным логарифмам имеем
 . Значит, полученные выше оценки числа шагов алгоритма Евклида в среднем завышены примерно в два с половиной раза. [4]
. Значит, полученные выше оценки числа шагов алгоритма Евклида в среднем завышены примерно в два с половиной раза. [4]2.4 Расширенный алгоритм Евклида
Пусть алгоритм Евклида на каждом шаге, кроме частного
 и остатка
и остатка 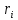 , вычисляет еще два значения
, вычисляет еще два значения  по правилу
по правилу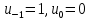
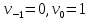
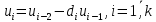
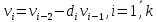
Такой алгоритм будет называться расширенным алгоритмом Евклида. В расширенном алгоритме Евклида для всех
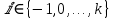 выполняется равенство
выполняется равенство 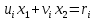 . Значение расширенного алгоритма Евклида состоит в том, что он дает линейное разложение наибольшего общего делителя
. Значение расширенного алгоритма Евклида состоит в том, что он дает линейное разложение наибольшего общего делителя 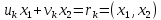 , которое играет важнейшую роль в операциях модульной арифметики.
, которое играет важнейшую роль в операциях модульной арифметики.Легко показать, что длина чисел
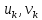 оценивается величиной
оценивается величиной 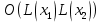 . Значит, сложность расширенного алгоритма Евклида отличается от сложности обычного алгоритма Евклида не более чем на константный множитель, т.е. для расширенного алгоритма Евклида сохраняется оценка сложности
. Значит, сложность расширенного алгоритма Евклида отличается от сложности обычного алгоритма Евклида не более чем на константный множитель, т.е. для расширенного алгоритма Евклида сохраняется оценка сложности 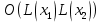 . [6]
. [6]2.5 Другие алгоритмы вычисления наибольшего общего делителя
Рассмотрим сначала один из простейших способов ускорения работы алгоритма Евклида. Пусть в ходе выполнения алгоритма вычисляются величины

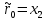
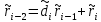 ,
, 
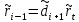
Здесь на