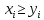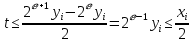Добавлен: 04.02.2024
Просмотров: 492
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-м шаге алгоритма сначала вычисляется остаток от деления
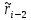на 
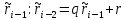, 0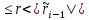
. Затем, если 
, то полагаем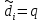 
, 
. Если же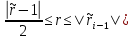 
, то полагаем
,
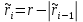В результате получаем равенство
, в котором
.
Нетрудно доказать, что в описанном алгоритме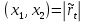
. Однако у описанного алгоритма по-другому оценивается количество шагов. Действительно, из условия 
, 
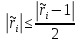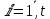следует, что 
. Значит, количество шагов алгоритма 
не превосходит 
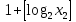. Эта оценка не сколько меньше оценки, полученной в теореме 1.3 для алгоритма Евклида. Вместе с тем общая оценка сложности алгоритма 
не изменяется.
Имеется целый ряд алгоритмов вычисления наибольшего общего делителя, в которых операция деления с остатком заменена на операцию деления с остатком на степени двойки. Поскольку данная операция для чисел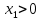
, представленных в 
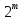-ичной системе счисления выполняется всего за 
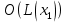операций, то достигается выигрыш в сложности каждого шага алгоритма. Однако обычно число шагов данных алгоритмов оказывается больше числа шагов алгоритма Евклида. [3]
Для чисел
сложности таких алгоритмов вычисления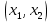
обычно оценивается величиной 
, однако экспериментальные данные свидетельствуют о том, что данные алгоритмы на 20-25% эффективнее алгоритма Евклида.
Пусть даны целые числа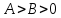
. Опишем сначала сам LSBGCD-алгоритм. Вычисляется последовательность упорядоченных пар 
неотрицательных чисел, где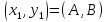 
, и если уже вычислена пара 
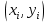, то:
Алгоритм заканчивает свою работу, как только очередное значение
оказывается равным нулю. При этом наибольшим общим делителем чисел 
и 
является число 
.
Убедимся в корректности приведенного алгоритма.
Утверждение 1.2. Пусть даны целые числа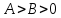 . LSBGCD алгоритм правильно вычисляет наибольший общий делитель чисел и за конечное число шагов. Доказательство. Во-первых, из описания LSBGCD алгоритма нетрудно увидеть, что на 
-м шаге алгоритма выполняются неравенства
Покажем, что число шагов алгоритма конечно. Из описания LSBGCD-алгоритма видно, что
. Кроме того неравенство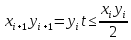 
. Значит, найдется 
, для которого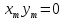 
. Отсюда следует, что 
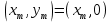, и LSBGCD-алгоритм выполняется за конечное число шагов.
Теперь индукцией по докажем, что на каждом шаге алгоритма наибольший общий делитель чисел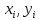 
равен наибольшему общему делителю 
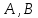. Равенство 
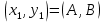очевидно. Рассмотрим теперь пару 
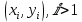. Не ограничивая общности, будем считать, что в ходе выполнения -го шага алгоритма не проводилась перестановка чисел в паре, т.е. 
, а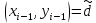 
. Тогда 
и, следовательно, 
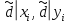. Значит, 
. С другой стороны, из условий, 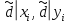следует, что, 
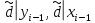.Значит, 
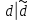. В итоге получаем, 
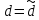, т.е. 
.
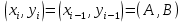Воспользовавшись доказанным равенством для
, видим, что
Подсчитаем сложность LSBGCD-алгоритма. Из описания алгоритма видно, что на -м шаге выполняются только вычитания чисел, умножения на степень двойки, а также сравниваются между собой числа. Поэтому сложность выполнения
-го шага можно оценить как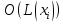 
. Кроме того, из неравенства 
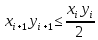, вытекает, что
.
Значит,
. Данная оценка числа шагов LSBGCD-алгоритма позволяет получить общую оценку его сложности в виде 
. [8]
Уроки математики углубляют и расширяют знания обучающихся, а также способствуют развитию их интереса к предмету, развитию математических способностей, привитию обучающимся интереса к самостоятельным занятиям математикой, воспитанию и развитию личной инициативы и творческих особенностей.
Изучение и углубление знаний по теме «Многочлены» является достаточно необходимым действием, которое позволяет значительно увеличить ценность современного образования и развить способности и стремления обучающихся к научно-исследовательской, а также познавательной деятельности.
Тема «многочлены» в курсе алгебры основной школы является одной из наиболее важных тем. Она лежит в основе при изучении формул сокращенного умножения, преобразований выражений и всех других типов выражений. Данная тема широко представлена и на государственных экзаменах, таких как ОГЭ и ЕГЭ.
В ходе работы над данной работой были получены следующие результаты:
Данная курсовая работа расширит кругозор студентов и обучающихся, которые изучают предмет «Алгебра», также она может быть полезна для учителей математики, для проведения элективных занятий в старшей школе (10-11 класс), профильных классах, с углубленным изучением математических наук.
Таким образом можно сделать вывод, что цель работы достигнута в полной мере, а задачи реализованы.
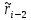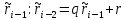на , 0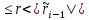 . Затем, если , то полагаем 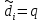, . Если же 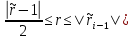, то полагаем 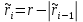, В результате получаем равенство
, в котором .Нетрудно доказать, что в описанном алгоритме
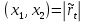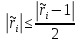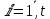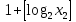. Однако у описанного алгоритма по-другому оценивается количество шагов. Действительно, из условия , следует, что . Значит, количество шагов алгоритма не превосходит . Эта оценка не сколько меньше оценки, полученной в теореме 1.3 для алгоритма Евклида. Вместе с тем общая оценка сложности алгоритма не изменяется.Имеется целый ряд алгоритмов вычисления наибольшего общего делителя, в которых операция деления с остатком заменена на операцию деления с остатком на степени двойки. Поскольку данная операция для чисел
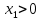, представленных в 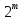-ичной системе счисления выполняется всего за 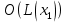операций, то достигается выигрыш в сложности каждого шага алгоритма. Однако обычно число шагов данных алгоритмов оказывается больше числа шагов алгоритма Евклида. [3]Для чисел
сложности таких алгоритмов вычисления
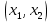обычно оценивается величиной , однако экспериментальные данные свидетельствуют о том, что данные алгоритмы на 20-25% эффективнее алгоритма Евклида.Пусть даны целые числа
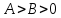. Опишем сначала сам LSBGCD-алгоритм. Вычисляется последовательность упорядоченных пар неотрицательных чисел, где 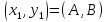, и если уже вычислена пара 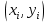, то:-
Находится число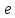
свойством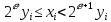 
-
Вычисляется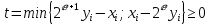
-
Если при этом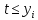
, то полагаем 
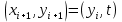, а если 
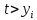, то полагаем 
.
Алгоритм заканчивает свою работу, как только очередное значение
оказывается равным нулю. При этом наибольшим общим делителем чисел и является число .Убедимся в корректности приведенного алгоритма.
Утверждение 1.2. Пусть даны целые числа
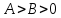. LSBGCD алгоритм правильно вычисляет наибольший общий делитель чисел и за конечное число шагов. Доказательство. Во-первых, из описания LSBGCD алгоритма нетрудно увидеть, что на -м шаге алгоритма выполняются неравенства
Покажем, что число шагов алгоритма конечно. Из описания LSBGCD-алгоритма видно, что
. Кроме того неравенство 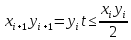. Значит, найдется , для которого 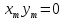. Отсюда следует, что 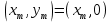, и LSBGCD-алгоритм выполняется за конечное число шагов.Теперь индукцией по
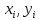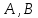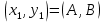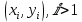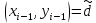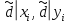докажем, что на каждом шаге алгоритма наибольший общий делитель чисел равен наибольшему общему делителю . Равенство очевидно. Рассмотрим теперь пару . Не ограничивая общности, будем считать, что в ходе выполнения -го шага алгоритма не проводилась перестановка чисел в паре, т.е. , а . Тогда и, следовательно, . Значит, . С другой стороны, из условий, 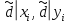следует, что, 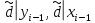.Значит, 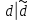. В итоге получаем, 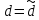, т.е. 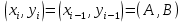.Воспользовавшись доказанным равенством для
, видим, что Подсчитаем сложность LSBGCD-алгоритма. Из описания алгоритма видно, что на
-м шаге выполняются только вычитания чисел, умножения на степень двойки, а также сравниваются между собой числа. Поэтому сложность выполнения
-го шага можно оценить как 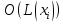. Кроме того, из неравенства 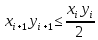, вытекает, что .Значит,
. Данная оценка числа шагов LSBGCD-алгоритма позволяет получить общую оценку его сложности в виде . [8]Заключение
Уроки математики углубляют и расширяют знания обучающихся, а также способствуют развитию их интереса к предмету, развитию математических способностей, привитию обучающимся интереса к самостоятельным занятиям математикой, воспитанию и развитию личной инициативы и творческих особенностей.
Изучение и углубление знаний по теме «Многочлены» является достаточно необходимым действием, которое позволяет значительно увеличить ценность современного образования и развить способности и стремления обучающихся к научно-исследовательской, а также познавательной деятельности.
Тема «многочлены» в курсе алгебры основной школы является одной из наиболее важных тем. Она лежит в основе при изучении формул сокращенного умножения, преобразований выражений и всех других типов выражений. Данная тема широко представлена и на государственных экзаменах, таких как ОГЭ и ЕГЭ.
В ходе работы над данной работой были получены следующие результаты:
-
В первой главе рассмотрены общие сведения о многочленах. -
Во второй главе более углубленно рассмотрены НОД, НОК, алгоритм Евклида и способы решения заданий с его помощью.
Данная курсовая работа расширит кругозор студентов и обучающихся, которые изучают предмет «Алгебра», также она может быть полезна для учителей математики, для проведения элективных занятий в старшей школе (10-11 класс), профильных классах, с углубленным изучением математических наук.
Таким образом можно сделать вывод, что цель работы достигнута в полной мере, а задачи реализованы.
Список используемой литературы
-
Алимов, Ш.А. Алгебра. 8 класс: учебник для общеобразовательных учреждений/ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. −21-изд. – М.: Просвещение, 2014. – 255 с.: ил. -
Алимов, Ш.А. Алгебра. 9 класс: учебник для общеобразовательных учреждений/ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. −17-изд. – М.: Просвещение, 2012. – 287 с.: ил. -
Булычева Ю. В., Васильева Т. В., Карпасюк И. В.Алгебра (Булычева, Ю. В. Алгебра : учебное пособие / Ю. В. Булычева, Т. В. Васильева, И. В. Карпасюк. — 2-е изд. — Астрахань : АГТУ, 2020. — ISBN 978-5-89154-699-8. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/195063 (дата обращения: 06.02.2023). — Режим доступа: для авториз. пользователей. — С. 13.). -
Булычева Ю. В., Васильева Т. В., Карпасюк И. В.Алгебра (Булычева, Ю. В. Алгебра : учебное пособие / Ю. В. Булычева, Т. В. Васильева, И. В. Карпасюк. — 2-е изд. — Астрахань : АГТУ, 2020. — ISBN 978-5-89154-699-8. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/195063 (дата обращения: 08.02.2023). — Режим доступа: для авториз. пользователей. — С. 162.). -
Виленкин, Н.Я. Алгебра. 8 класс [Текст]: учебное пособие для учащихся школ и классов с углубленным изучением математики/ Н.Я. Вилен-кин, А.Н. Виленкин, Г.С. Суворов, Ю.А. Дробышев, И.В. Дробышева, А.И.Кудрявцев; под ред. Н.Я Виленкин. – М.: Просвещение, 1998. – 235 с -
Глухов М. М., Круглов И. А., Пичкур А. Б., Черемушкин А. В.Введение в теоретико-числовые методы криптографии (Введение в теоретико-числовые методы криптографии : учебное пособие / М. М. Глухов, И. А. Круглов, А. Б. Пичкур, А. В. Черемушкин. — Санкт-Петербург : Лань, 2022. — ISBN 978-5-8114-1116-0. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/210746 (дата обращения: 04.02.2023). — Режим доступа: для авториз. пользователей. — С. 16.). -
Глухов М. М., Круглов И. А., Пичкур А. Б., Черемушкин А. В.Введение в теоретико-числовые методы криптографии (Введение в теоретико-числовые методы криптографии : учебное пособие / М. М. Глухов, И. А. Круглов, А. Б. Пичкур, А. В. Черемушкин. — Санкт-Петербург : Лань, 2022. — ISBN 978-5-8114-1116-0. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/210746 (дата обращения: 07.02.2023). — Режим доступа: для авториз. пользователей. — С. 18.). -
Жук Л. В., Прокуратова О. Н.Практикум по алгебре многочленов. Часть I (Жук, Л. В. Практикум по алгебре многочленов : учебное пособие / Л. В. Жук, О. Н. Прокуратова. — Елец : ЕГУ им. И.А. Бунина, 2019 — Часть 1 — 2019. — 76 с. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/196020 (дата обращения: 04.02.2023). — Режим доступа: для авториз. пользователей. — С. 40.). -
Звягин А. В.Курс лекций по алгебре. Многочлены (Звягин, А. В. Курс лекций по алгебре. Многочлены : учебно-методическое пособие / А. В. Звягин. — Воронеж : ВГУ, 2018. — 50 с. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/171159 (дата обращения: 08.02.2023). — Режим доступа: для авториз. пользователей. — С. 20.). -
Игонина Е. В., Прокуратова О. Н.Лекции по теории многочленов (Игонина, Е. В. Лекции по теории многочленов : учебное пособие / Е. В. Игонина, О. Н. Прокуратова. — Елец : ЕГУ им. И.А. Бунина, 2016. — 85 с. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/195890 (дата обращения: 06.02.2023). — Режим доступа: для авториз. пользователей. — С. 17.). -
Крючкова, В.В. Об опыте работы с правилами в теме «Многочлены»/ В.В. Крючкова//Математика в школе. - 1984. - № 5. – С. 38–39. -
Мартынов Л. М.Алгебра и теория чисел для криптографии (Мартынов, Л. М. Алгебра и теория чисел для криптографии : учебное пособие для вузов / Л. М. Мартынов. — 2-е изд., стер. — Санкт-Петербург : Лань, 2022. — ISBN 978-5-8114-9346-3. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/189446 (дата обращения: 05.02.2023). — Режим доступа: для авториз. пользователей. — С. 171.). -
Рыбин С. В.Дискретная математика и информатика (Рыбин, С. В. Дискретная математика и информатика : учебник для вузов / С. В. Рыбин. — Санкт-Петербург : Лань, 2022. — ISBN 978-5-8114-8566-6. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/193326 (дата обращения: 06.02.2023). — Режим доступа: для авториз. пользователей. — С. 116.). -
Сикорская Г.А. Алгебра и теория чисел (Сикорская, Г. А. Алгебра и теория чисел : учебное пособие / Г. А. Сикорская. — Оренбург : ОГУ, 2017. — ISBN 978-5-7410-1975-8. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/110642 (дата обращения: 08.02.2023). — Режим доступа: для авториз. пользователей. — С. 52.). -
Тропин М. П. Основы прикладной алгебры (Тропин, М. П. Основы прикладной алгебры : учебное пособие / М. П. Тропин. — 2-е изд., стер. — Санкт-Петербург : Лань, 2020. — ISBN 978-5-8114-5327-6. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/139282 (дата обращения: 08.02.2023). — Режим доступа: для авториз. пользователей. — С. 101.). -
Черемисина М. И.Избранные вопросы алгебры и теории чисел. Многочлены (Черемисина, М. И. Избранные вопросы алгебры и теории чисел. Многочлены : учебное пособие / М. И. Черемисина. — Оренбург : ОГПУ, 2021. — 65 с. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/179894 (дата обращения: 07.02.2023). — Режим доступа: для авториз. пользователей. — С. 12.).