Добавлен: 04.02.2024
Просмотров: 494
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Глава 2. Наименьшее общее кратное, наибольший общий делитель. Алгоритм Евклида
2.1 Наибольший общий делитель
Пусть
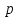 и
и 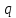 - многочлены с коэффициентами в целочисленной области
- многочлены с коэффициентами в целочисленной области  , обычно поле или целые числа. Наибольший общий делитель
, обычно поле или целые числа. Наибольший общий делитель 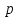 и
и 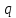 - это многочлен
- это многочлен 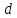 , который делит
, который делит 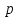 и
и 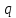 , и такой, что каждый общий делитель
, и такой, что каждый общий делитель 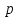 и
и 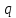 также делит
также делит 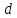 . Каждая пара многочленов (не оба равны нулю) имеет GCD тогда и только тогда, когда
. Каждая пара многочленов (не оба равны нулю) имеет GCD тогда и только тогда, когда  является уникальной областью факторизации.
является уникальной областью факторизации.Если
 является полем, а
является полем, а 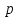 и
и 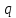 не равны нулю, многочлен
не равны нулю, многочлен 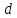 является наибольшим общим делителем тогда и только тогда, когда он делит как
является наибольшим общим делителем тогда и только тогда, когда он делит как 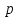 , так и
, так и 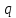 , и он имеет наибольшую степень среди многочленов, обладающих этим свойством. Если
, и он имеет наибольшую степень среди многочленов, обладающих этим свойством. Если  НОД равен 0. Однако некоторые авторы считают
НОД равен 0. Однако некоторые авторы считают
, что в данном случае он не определен.
Наибольший общий делитель
 и
и  обычно обозначается как
обычно обозначается как 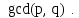
Наибольший общий делитель не является уникальным: если d является НОД из
 и
и  , то многочлен
, то многочлен  является другим НОД тогда и только тогда, когда существует обратимый элемент
является другим НОД тогда и только тогда, когда существует обратимый элемент  из
из  такой, что
такой, что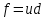
и
{\displaystyle d=u^{-1}f}
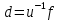
Другими словами, GCD уникален с точностью до умножения на обратимую константу.
В случае целых чисел эта неопределенность была решена путем выбора в качестве GCD единственного положительного (есть еще один, который является его противоположностью). Согласно этому соглашению, НОД двух целых чисел также является наибольшим (для обычного порядка) общим делителем. Однако, поскольку для многочленов над целочисленной областью не существует естественного общего порядка, здесь нельзя действовать таким же образом. Для одномерных многочленов над полем можно дополнительно потребовать, чтобы GCD был одномерным (то есть иметь 1 в качестве коэффициента наивысшей степени), но в более общих случаях общего соглашения нет.
Следовательно, равенства типа
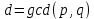 или
или  являются распространенными злоупотреблениями обозначениями, которые следует читать как "
являются распространенными злоупотреблениями обозначениями, которые следует читать как " -это GCD из
-это GCD из 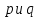 " и "
" и " и
и  имеют тот же набор GCD, что и
имеют тот же набор GCD, что и 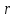
и
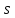 ". В частности,
". В частности, 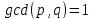 означает, что обратимые константы являются единственными общими делителями. В этом случае, по аналогии с целочисленным случаем, говорят, что
означает, что обратимые константы являются единственными общими делителями. В этом случае, по аналогии с целочисленным случаем, говорят, что  и
и  равны взаимно простые многочлены. [9]
равны взаимно простые многочлены. [9]2.2 Наименьшее общее кратное
Пусть даны многочлены
 и
и  над полем
над полем 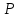 .
.Определение 1. Многочлен
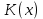 называется общим кратным многочленов
называется общим кратным многочленов  и
и  , если
, если 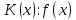 и
и 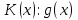 .
.Определение 2. Наибольшим общим кратным (НОК) многочленов
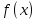 и
и  называется такое их общее кратное, на которое делится любое общее кратное этих многочленов.
называется такое их общее кратное, на которое делится любое общее кратное этих многочленов.Замечание. Наибольшим общим кратным (НОК) многочленов
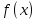 и
и  обозначается НОК (
обозначается НОК (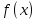 ,
,  ) или НОК
) или НОК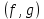 или
или  .
.Теорема 1. НОК многочленов
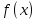 и
и  вычисляется по формуле:
вычисляется по формуле: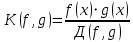 (1.6)
(1.6)Таким образом, НОК двух многочленов есть частное от деления произведения этих многочленов на их НОД.
Доказательство. Пусть НОД многочленов
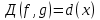 , тогда
, тогда  и
и  . Поставим в формулу 1.6 вместо
. Поставим в формулу 1.6 вместо  его значение, получим:
его значение, получим: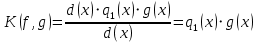
Следовательно,
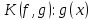 .
.В равенстве 1.6 подставим вместо
 его значение, получим:
его значение, получим: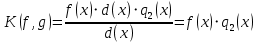
Следовательно,
 .
.Итак, многочлен
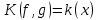 является общим кратным многочленов
является общим кратным многочленов  и
и  . Пусть
. Пусть  есть наименьшее общее кратное многочленов
есть наименьшее общее кратное многочленов  и
и  . Требуется доказать, что
. Требуется доказать, что 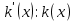 . Так как
. Так как  – общее кратное
– общее кратное  и
и  , то
, то 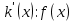 и
и 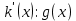 . Пусть
. Пусть  и
и 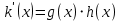 . Будем иметь, что
. Будем иметь, что 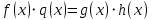 . Делим обе части последнего равенства на
. Делим обе части последнего равенства на  и получаем:
и получаем: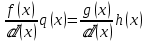
Многочлены
 и
и  делятся на свой НОД
делятся на свой НОД  , в частном получим взаимно простые многочлены
, в частном получим взаимно простые многочлены 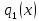 и
и 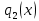 . Многочлен
. Многочлен  будет делиться на
будет делиться на  . Подставляя значение
. Подставляя значение 